[1] 125. 验证回文串【简单】
给定一个字符串,验证它是否是回文串,只考虑字母和数字字符,可以忽略字母的大小写。
说明:本题中,我们将空字符串定义为有效的回文串。
示例 1:
输入: "A man, a plan, a canal: Panama" 输出: true示例 2:
输入: "race a car" 输出: false
class Solution:
def isPalindrome(self, s: str) -> bool:
# 回文串,即正读和反读一样的字符串
# 去掉字符串中的空格和字符,那么字符串是对称的
s = "".join(filter(str.isalnum,s)).lower()
return s == s[::-1]
代码中的知识点:
filter() # python语言中的过滤函数
str.isalnum # 过滤函数满足的条件为,字母和数字
str.lower() # 将字符串中的字符转为小写
str.upper() # 将字符串中的字符转换为大写
chr() # 将数字转为字符,其中大写字母的范围为65——90,小写字母为97——122,数字为48——57
ord() # 将字符转为数字,与chr()相反
s == s[::-1] # 将字符串倒转
对于上述问题,首先想到的是字符的replace()函数,但是当字符串中的特殊字符太多,如果仅仅使用字符串的replace()函数难以实现。我们想到了 正则表达式。
re.compile() # 构建要匹配的模式,对于要匹配的模式,一种是找出字符串中的字母和数字;另一种是找出特殊字符作为分隔符
re.split() # 通过特殊字符串对字符串进行分割后合并,实验发现,可能结果太多了
re.findall() # 寻找字母和数字,匹配字符为"w",匹配的是单词字符[A-Za-z0-9_]
生成代码:
class Solution:
def isPalindrome(self, s: str) -> bool:
# 回文串,即正读和反读一样的字符串
# 去掉字符串中的空格和字符,那么字符串是对称的
import re
s = s.lower()
p = re.compile("w")
s = "".join(p.findall(s))
print(s)
return s == s[::-1]
[2] 859. 亲密字符串【简单】
给定两个由小写字母构成的字符串
A和B,只要我们可以通过交换A中的两个字母得到与B相等的结果,就返回true;否则返回false。示例 1:
输入: A = "ab", B = "ba" 输出: true示例 2:
输入: A = "ab", B = "ab" 输出: false 字符串相同,且重复的字符串小于2,返回False示例 3:
输入: A = "aa", B = "aa" 输出: true 字符串相同,且存在2个及两个以上的重复的字符串,返回True示例 4:
输入: A = "aaaaaaabc", B = "aaaaaaacb" 输出: true示例 5:
输入: A = "", B = "aa" 输出: false 长度不同,返回False提示:
0 <= A.length <= 200000 <= B.length <= 20000A和B仅由小写字母构成官方题解, 其实情况没有那么多, 就三种情况:
- 字符串长度不相等, 直接返回false
- 字符串相等的时候, 只要有重复的元素就返回true
- A, B字符串有不相等的两个地方, 需要查看它们交换后是否相等即可.
class Solution:
def buddyStrings(self, A: str, B: str) -> bool:
if len(A) != len(B):
return False
if A == B and len(set(A)) < len(A):
return True
resArr = []
for i in range(len(A)):
if A[i] != B[i]:
resArr.append(A[i]+B[i])
return True if len(resArr) == 2 and resArr[0] == resArr[1][::-1] else False
本题的难点是,难以从几个例题中抽象出本题的主旨。
[3] 557. 反转字符串中的单词 III【简单】
给定一个字符串,你需要反转字符串中每个单词的字符顺序,同时仍保留空格和单词的初始顺序。
示例 1:
输入: "Let's take LeetCode contest"
输出: "s'teL ekat edoCteeL tsetnoc"
注意:在字符串中,每个单词由单个空格分隔,并且字符串中不会有任何额外的空格。
# 一次提交
class Solution:
def reverseWords(self, s: str) -> str:
s_lst = list(s.split())
s_new = []
for i in s_lst:
s_new.append(i[::-1])
return " ".join(s_new)
# 二次提交
class Solution:
def reverseWords(self, s: str) -> str:
s_lst = list(s[::-1].split())
s_lst.reverse()
return " ".join(s_lst)
[4] 15. 三数之和【难】
给定一个包含 n 个整数的数组 nums,判断 nums 中是否存在三个元素 a,b,c ,使得 a + b + c = 0 ?找出所有满足条件且不重复的三元组。
注意:答案中不可以包含重复的三元组。
示例:
给定数组 nums = [-1, 0, 1, 2, -1, -4],
满足要求的三元组集合为:
[
[-1, 0, 1],
[-1, -1, 2]
]
在刷[这道题的过程中介于奔溃状态,好不容易处理好了 LeetCode 上的所有问题,但是,由于所写程序的时间复杂度超过了要求,还是没有执行成功。经过多番资料查找,对于列表较大的情况,往往双指针算法是最好的解决办法。
双指针:主要用于遍历数组,两个指针指向不同的元素,从而协同完成任务。双指针可以从不同的方向向中间逼近也可以朝着同一个方向遍历。
下面是找到的大佬的代码,供自己学习:
"""
使用双指针,一个指针指向值较小的元素,一个指针指向值较大的元素。
指向较小元素的指针从头向尾遍历,指向较大元素的指针从尾向头遍历。
如果两个指针指向元素的和 sum == target,那么得到要求的结果;
如果 sum > target,移动较大的元素,使 sum 变小一些;
如果 sum < target,移动较小的元素,使 sum 变大一些。
"""
class Solution:
def threeSum(self, nums: List[int]) -> List[List[int]]:
nums.sort()
res =[]
i = 0
for i in range(len(nums)):
if i == 0 or nums[i]>nums[i-1]:
l = i+1
r = len(nums)-1
while l < r:
s = nums[i] + nums[l] +nums[r]
if s ==0:
res.append([nums[i],nums[l],nums[r]])
l +=1
r -=1
while l < r and nums[l] == nums[l-1]:
l += 1
while r > l and nums[r] == nums[r+1]:
r -= 1
elif s>0:
r -=1
else :
l +=1
return res
[5] 215. 数组中的第K个最大元素
在未排序的数组中找到第 k 个最大的元素。请注意,你需要找的是数组排序后的第 k 个最大的元素,而不是第 k 个不同的元素。
示例 1:
输入: [3,2,1,5,6,4] 和 k = 2
输出: 5
示例 2:
输入: [3,2,3,1,2,4,5,5,6] 和 k = 4
输出: 4
代码实现
# 利用堆实现
import heapq
class Solution:
def findKthLargest(self, nums: List[int], k: int) -> int:
lst = heapq.nlargest(k,nums)
return sorted(lst)[0]
[6]面试题24. 反转链表【中】
定义一个函数,输入一个链表的头节点,反转该链表并输出反转后链表的头节点。
示例:
输入: 1->2->3->4->5->NULL
输出: 5->4->3->2->1->NULL
ListNode{val: 1, next: ListNode{val: 2, next: ListNode{val: 3, next: ListNode{val: 4, next: ListNode{val: 5, next: None}}}}}
限制:
0 <= 节点个数 <= 5000
class Solution:
def reverseList(self, head: ListNode) -> ListNode:
preNode = None
currNode = head
while currNode:
nextNode = currNode.next
currNode.next = preNode
preNode = currNode
currNode = nextNode
return preNode
# Definition for singly-linked list.
# class ListNode:
# def __init__(self, x):
# self.val = x
# self.next = None
class Solution:
"""
对于所有的步骤,相当于一分为二的一个迭代过程first,second
外加一个中间存储介质memory
"""
def reverseList(self, head: ListNode) -> ListNode:
first, memory = None, head # 看作第一次切分,前一步分first为None,有一部分暂时给他放在memeory中
while memory != None:
second = memory.next # 新的一次切分
memory.next = first # 将旧的加入first到新的中first中
first = memory
memory = second # 为下一次切分做准备,同时作为判断条件,当切分到最后时,只有[1,2,3,4,5]与None
return first
[7]3. 无重复字符的最长子串【难】
给定一个字符串,请你找出其中不含有重复字符的 最长子串 的长度。
示例 1:
输入: "abcabcbb"
输出: 3
解释: 因为无重复字符的最长子串是 "abc",所以其长度为 3。
示例 2:
输入: "bbbbb"
输出: 1
解释: 因为无重复字符的最长子串是 "b",所以其长度为 1。
示例 3:
输入: "pwwkew"
输出: 3
解释: 因为无重复字符的最长子串是 "wke",所以其长度为 3。
请注意,你的答案必须是 子串 的长度,"pwke" 是一个子序列,不是子串。
class Solution:
def lengthOfLongestSubstring(self, s: str) -> int:
st = {}
# st字典用于存放字符串中各个字母的位置的下一个位置,
# 如果出现重复字母时,从前面的子串中找到与该字母重复的字母的位置
# 同时将该查找到重复字母的下一个位置作为下一个子串的起始位置
i, ans = 0, 0 # i,起始位置;
for j in range(len(s)): # j,末位置
if s[j] in st:
i = max(st[s[j]], i)
ans = max(ans, j - i +1 ) # ans,遍历过程中子串的最大长度;
st[s[j]] = j + 1 # st字典用于存放字符串中各个字母的位置的下一个位置,
return ans;
[7附加]面试题51. 数组中的逆序对【困难】
在数组中的两个数字,如果前面一个数字大于后面的数字,则这两个数字组成一个逆序对。输入一个数组,求出这个数组中的逆序对的总数。
示例 1:
输入: [7,5,6,4]
输出: 5
class Solution:
def reversePairs(self, nums: List[int]) -> int:
"""利用归并排序merge思想,每个即将merge的数组是有序的来判断前大后小的种类个数"""
self.res = 0
self.merge_sort(nums, 0, len(nums) - 1)
return self.res
def merge_sort(self, nums, l, r):
"""左闭右闭"""
if l >= r:
return
mid = l + (r - l) // 2
self.merge_sort(nums, l, mid)
self.merge_sort(nums, mid + 1, r)
self.merge(nums, l, mid, r)
def merge(self, nums, l, mid, r):
aux = nums[l: r + 1]
idx1, idx2 = l, mid + 1
for k in range(l, r + 1):
if idx1 > mid:
nums[k] = aux[idx2 - l]
idx2 += 1
elif idx2 > r:
nums[k] = aux[idx1 - l]
idx1 += 1
elif aux[idx1 - l] <= aux[idx2 - l]:
nums[k] = aux[idx1 - l]
idx1 += 1
else:
# 此时是大于的条件
self.res += mid - idx1 + 1
nums[k] = aux[idx2 - l]
idx2 += 1
class Solution:
def removeNthFromEnd(self, head: ListNode, n: int) -> ListNode:
later_p=head
poineer_p=head
while n :
n-=1
poineer_p=poineer_p.next
if poineer_p==None:
head=head.next
return head
while poineer_p.next!=None:
poineer_p=poineer_p.next
later_p=later_p.next
later_p.next=later_p.next.next
return head
class Solution:
def reversePairs(self, nums: List[int]) -> int:
self.count = 0
def merge(lfrom, lto, low, mid, high):
'''
lfrom:要归并的表
lto:要存入的表
low:归并段的开始
mid:归并段中间
high:归并段结束'''
i, j, k = low, mid, low
while i < mid and j < high: # 反复复制两分段首记录中较小的
if lfrom[i] <= lfrom[j]:
lto[k] = lfrom[i]
i += 1
k += 1
else:
lto[k] = lfrom[j]
self.count += mid - i
j += 1
k += 1
while i < mid: # 复制第一段剩余记录
lto[k] = lfrom[i]
i += 1
k += 1
while j < high: # 复制第二段剩余记录
lto[k] = lfrom[j]
j += 1
k += 1
def merge_pass(lfrom, lto, llen, slen):
'''
llen:表长度
slen:分段长度
'''
i = 0
while i+2*slen < llen: # 归并这两段
merge(lfrom, lto, i, i+slen, i+2*slen)
i += 2*slen
if i+slen < llen: # 后端长度不足slen
merge(lfrom, lto, i, i+slen, llen)
else: # 只剩下一段的情况,整段复制过去
for j in range(i, llen):
lto[j] = lfrom[j]
def merge_sort(lst):
slen, llen = 1, len(lst)
templst = [None]*llen
while slen < llen:
merge_pass(lst, templst, llen, slen)
slen *= 2
merge_pass(templst, lst, llen, slen) # 每一次都让结果存回原位
slen *= 2
return self.count
return merge_sort(nums)
[8] 148. 排序链表【中等】递归
在 O(n log n) 时间复杂度和常数级空间复杂度下,对链表进行排序。
示例 1:
输入: 4->2->1->3
输出: 1->2->3->4
示例 2:
输入: -1->5->3->4->0
输出: -1->0->3->4->5
示例代码:
class Solution:
def sortList(self, head: ListNode) -> ListNode:
# [1,3,2,4,6,5,7]
if not head or not head.next:return head
mid = self.getmid(head)
rhead ,mid.next= mid.next,None # [6,5,7],[4]
return self.mergesort(self.sortList(head),self.sortList(rhead))
def getmid(self,head):
# 双指针,slow = [1,2,3]
if not head:return head
slow = fast = head
while fast.next and fast.next.next:fast,slow = fast.next.next,slow.next
return slow
def mergesort(self,lhead,rhead):
dummy = cur = ListNode(0)
while lhead and rhead:
if lhead.val <= rhead.val:cur.next,lhead = lhead,lhead.next
else:cur.next ,rhead= rhead,rhead.next
cur = cur.next
cur.next = lhead or rhead
return dummy.next
[8附加]23. 合并K个排序链表【困难】递归
合并 k 个排序链表,返回合并后的排序链表。请分析和描述算法的复杂度。
示例:
输入:
[
1->4->5,
1->3->4,
2->6
]
输出: 1->1->2->3->4->4->5->6
class Solution:
def mergeKLists(self, lists: List[ListNode]) -> ListNode:
if not lists:return
n = len(lists)
return self.merge(lists, 0, n-1)
def merge(self,lists, left, right):
if left == right:
return lists[left]
mid = left + (right - left) // 2
l1 = self.merge(lists, left, mid)
l2 = self.merge(lists, mid+1, right)
return self.mergeTwoLists(l1, l2)
def mergeTwoLists(self,l1, l2):
if not l1:return l2
if not l2:return l1
if l1.val < l2.val:
l1.next = self.mergeTwoLists(l1.next, l2)
return l1
else:
l2.next = self.mergeTwoLists(l1, l2.next)
return l2
[9]82. 删除排序链表中的重复元素 II
给定一个排序链表,删除所有含有重复数字的节点,只保留原始链表中 没有重复出现 的数字。
示例 1:
输入: 1->2->3->3->4->4->5
输出: 1->2->5
示例 2:
输入: 1->1->1->2->3
输出: 2->3
示例代码:
class Solution(object):
def deleteDuplicates(self, head):
if head==None or head.next==None:
return head
# 构建一个字典,并且记录每个字母在字符串中出现的个数
dict1=dict()
p1=head
while p1:
if p1.val not in dict1:
dict1[p1.val]=1
else:
dict1[p1.val]+=1
p1=p1.next
# 看看是否每个字符都重复,如果都重复,就没有必要去除了,也可以看成是找到第一个没重复的元素位置
# 如果都重复了,也就会出现下一步骤的head == None
p1=head
while p1:
if dict1[p1.val]>1:
p1=p1.next
else:
break
# 由于第一个就没重复,所以从第一个开始
head=p1
if head==None:
return head # 故障排除,不是通过break结束循环的,用于[1,1,2,2,3,3]
if head.next==None: # 故障排除,[1,1,2,2,3]
if dict1[head.val]>1: # 感觉这个步骤用不上,经试验,确实没用
return None
else:
return head
# 上面的两种情况已处理,对于一般情况,如[1,2,3,3,4,4,5]
p1=head # [1,2,3,3,4,4,5]
p2=head.next # [2,3,3,4,4,5]
# p1 与 p2相当于快慢指针,一前一后,用后面的指针来确定何时终止
while 1:
if dict1[p2.val]>1:
p2=p2.next
p1.next=p2 # 此处p2后移,p1不动
else:
p1=p1.next
p2=p2.next
if p2==None:
return head # 此处,通过p1更新head
[9附加]19. 删除链表的倒数第N个节点【中等】
给定一个链表,删除链表的倒数第 n 个节点,并且返回链表的头结点。
示例:
给定一个链表: 1->2->3->4->5, 和 n = 2.
当删除了倒数第二个节点后,链表变为 1->2->3->5.
说明:
给定的 n 保证是有效的。
进阶:
你能尝试使用一趟扫描实现吗?
示例代码:
class Solution:
## 很巧妙的双指针
def removeNthFromEnd(self, head: ListNode, n: int) -> ListNode:
a = head
b = head
for i in range(n):
if a.next :
a = a.next
else:
return head.next
while a.next:
a = a.next
b = b.next
b.next = b.next.next
return head
[10]面试题35. 复杂链表的复制【中等】递归
请实现 copyRandomList 函数,复制一个复杂链表。在复杂链表中,每个节点除了有一个 next 指针指向下一个节点,还有一个 random 指针指向链表中的任意节点或者 null。
示例 1:
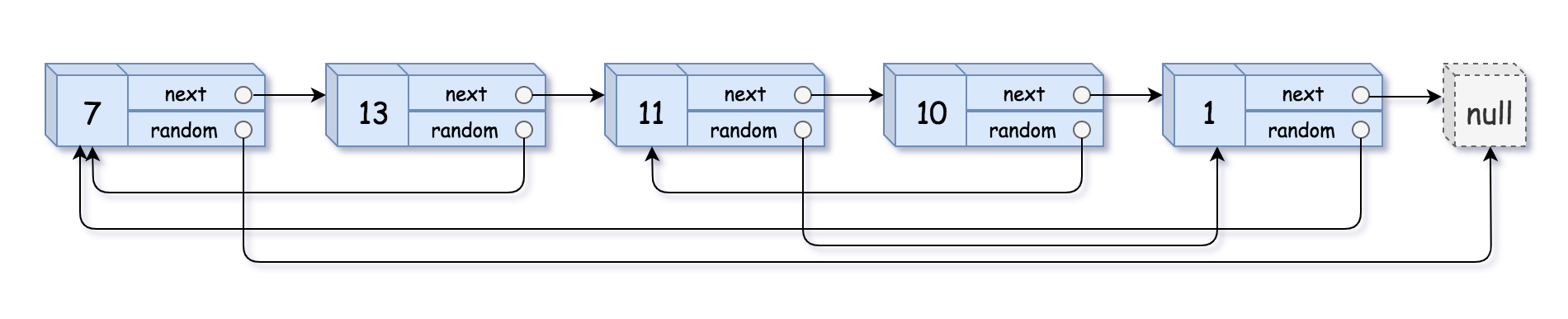
输入:head = [[7,null],[13,0],[11,4],[10,2],[1,0]]
输出:[[7,null],[13,0],[11,4],[10,2],[1,0]]
示例 2:

输入:head = [[1,1],[2,1]]
输出:[[1,1],[2,1]]
示例 3:

输入:head = [[3,null],[3,0],[3,null]]
输出:[[3,null],[3,0],[3,null]]
示例 4:
输入:head = []
输出:[]
解释:给定的链表为空(空指针),因此返回 null。
提示:
-10000 <= Node.val <= 10000Node.random为空(null)或指向链表中的节点。- 节点数目不超过 1000 。
示例代码:
# 深度优先搜索
class Solution:
def copyRandomList(self, head: 'Node') -> 'Node':
def dfs(head):
if not head: return None
if head in visited:
return visited[head]
# 创建新结点
copy = Node(head.val, None, None)
visited[head] = copy # 新旧之间的对应关系
copy.next = dfs(head.next)
copy.random = dfs(head.random) # 字典似乎是为random建立的,可以反向搜索
return copy
visited = {} # 放不同的节点
return dfs(head) # 返回最外层的
# 广度优先搜索
class Solution:
def copyRandomList(self, head: 'Node') -> 'Node':
visited = {}
def bfs(head):
if not head: return head
clone = Node(head.val, None, None) # 创建新结点
queue = collections.deque()
queue.append(head)
visited[head] = clone
while queue:
tmp = queue.pop()
if tmp.next and tmp.next not in visited:
visited[tmp.next] = Node(tmp.next.val, [], [])
queue.append(tmp.next)
if tmp.random and tmp.random not in visited:
visited[tmp.random] = Node(tmp.random.val, [], [])
queue.append(tmp.random)
visited[tmp].next = visited.get(tmp.next)
visited[tmp].random = visited.get(tmp.random)
return clone
return bfs(head)
[10附加]138. 复制带随机指针的链表【中等】
给定一个链表,每个节点包含一个额外增加的随机指针,该指针可以指向链表中的任何节点或空节点。
要求返回这个链表的 深拷贝。
我们用一个由 n 个节点组成的链表来表示输入/输出中的链表。每个节点用一个 [val, random_index] 表示:
val:一个表示Node.val的整数。random_index:随机指针指向的节点索引(范围从0到n-1);如果不指向任何节点,则为null。
示例 1:

输入:head = [[7,null],[13,0],[11,4],[10,2],[1,0]]
输出:[[7,null],[13,0],[11,4],[10,2],[1,0]]
示例 2:

输入:head = [[1,1],[2,1]]
输出:[[1,1],[2,1]]
示例 3:

输入:head = [[3,null],[3,0],[3,null]]
输出:[[3,null],[3,0],[3,null]]
示例 4:
输入:head = []
输出:[]
解释:给定的链表为空(空指针),因此返回 null。
提示:
-10000 <= Node.val <= 10000Node.random为空(null)或指向链表中的节点。
class Solution:
def copyRandomList(self, head: 'Node') -> 'Node':
def dfs(head):
if not head: return None
if head in visited:
return visited[head]
# 创建新结点
copy = Node(head.val, None, None)
visited[head] = copy # 新旧之间的对应关系
copy.next = dfs(head.next)
copy.random = dfs(head.random) # 字典似乎是为random建立的,可以反向搜索
return copy
visited = {} # 放不同的节点
return dfs(head) # 返回最外层的
[11]110. 平衡二叉树
难度简单252收藏分享切换为英文关注反馈
给定一个二叉树,判断它是否是高度平衡的二叉树。
本题中,一棵高度平衡二叉树定义为:
一个二叉树每个节点 的左右两个子树的高度差的绝对值不超过1。
示例 1:
给定二叉树 [3,9,20,null,null,15,7]
3
/
9 20
/
15 7
返回 true 。
示例 2:
给定二叉树 [1,2,2,3,3,null,null,4,4]
1
/
2 2
/
3 3
/
4 4
返回 false 。
示例代码
# Definition for a binary tree node.
# class TreeNode:
# def __init__(self, x):
# self.val = x
# self.left = None
# self.right = None
class Solution:
# 可以从叶子到根节点反着理解
def isBalanced(self, root: TreeNode) -> bool:
def height(root):
if root == None: return 0 # 临界条件
lh = height(root.left)
rh = height(root.right)
if lh >= 0 and rh >= 0 and abs(lh-rh) <= 1:
return max(lh,rh)+1
else:
return -1
return height(root)>=0
[11附加题]面试题07. 重建二叉树【中等】
输入某二叉树的前序遍历和中序遍历的结果,请重建该二叉树。假设输入的前序遍历和中序遍历的结果中都不含重复的数字。
例如,给出
前序遍历 preorder = [3,9,20,15,7]
中序遍历 inorder = [9,3,15,20,7]
返回如下的二叉树:
3
/
9 20
/
15 7
限制:
0 <= 节点个数 <= 5000
class Solution:
def buildTree(self, preorder: List[int], inorder: List[int]) -> TreeNode:
def re_construct_BTree(preorder,inorder):
# 前序遍历和中序遍历长度一致
if len(preorder) != len(inorder) or len(preorder)<1:
return None
if len(preorder) == 1:
return TreeNode(preorder[0],None,None)
root_node = preorder[0]
root_tree = TreeNode(root_node)
in_root_node_index = inorder.index(root_node)
# 左子树
pre_l_child_tree = preorder[1:in_root_node_index+1]
in_l_child_tree = inorder[:in_root_node_index]
root_tree.left = re_construct_BTree(pre_l_child_tree, in_l_child_tree)
# 右子树
pre_r_child_tree = preorder[in_root_node_index+1:]
in_r_child_tree = inorder[in_root_node_index+1:]
root_tree.right = re_construct_BTree(pre_r_child_tree, in_r_child_tree)
return root_tree
[12]面试题27. 二叉树的镜像【简单】
请完成一个函数,输入一个二叉树,该函数输出它的镜像。
例如输入:
4
/
2 7
/ /
1 3 6 9
镜像输出:
4
/
7 2
/ /
9 6 3 1
示例 1:
输入:root = [4,2,7,1,3,6,9]
输出:[4,7,2,9,6,3,1]
限制:
0 <= 节点个数 <= 1000
示例代码:
# Definition for a binary tree node.
# class TreeNode:
# def __init__(self, x):
# self.val = x
# self.left = None
# self.right = None
class Solution:
def mirrorTree(self, root: TreeNode) -> TreeNode:
def cross_tree(root):
if root == None: return None
if root.left == None and root.right == None:
return TreeNode(root.val)
new_tree = TreeNode(root.val)
new_tree.left = cross_tree(root.right)
new_tree.right = cross_tree(root.left)
return new_tree
return cross_tree(root)
执行用时 :64 ms, 在所有 Python3 提交中击败了8.37%的用户
内存消耗 :13.5 MB, 在所有 Python3 提交中击败了100.00%的用户
主要问题在于,创建了一个函数;而且完成了对树的
深拷贝,本题中我们只需要在原来的基础上修改就好。
更新代码
# Definition for a binary tree node.
# class TreeNode:
# def __init__(self, x):
# self.val = x
# self.left = None
# self.right = None
class Solution:
def mirrorTree(self, root: TreeNode) -> TreeNode:
if root == None: return None
root.left,root.right = root.right, root.left
self.mirrorTree(root.left)
self.mirrorTree(root.right)
return root
执行用时:32 ms
内存消耗:13.6 MB
[12附加]面试题26. 树的子结构[中等]
输入两棵二叉树A和B,判断B是不是A的子结构。(约定空树不是任意一个树的子结构)
B是A的子结构, 即 A中有出现和B相同的结构和节点值。
例如:
给定的树 A:
3 / 4 5 / 1 2
给定的树 B:
4 / 1
返回 true,因为 B 与 A 的一个子树拥有相同的结构和节点值。
示例 1:
输入:A = [1,2,3], B = [3,1]
输出:false
示例 2:
输入:A = [3,4,5,1,2], B = [4,1]
输出:true
限制:
0 <= 节点个数 <= 10000
# Definition for a binary tree node.
# class TreeNode:
# def __init__(self, x):
# self.val = x
# self.left = None
# self.right = None
class Solution:
def isSubStructure(self, A: TreeNode, B: TreeNode) -> bool:
if B == None: return False
if A == None: return False
# 经过这两个条件的筛选,A,B两棵树的不可能为None
# 下面需要考虑子结构为None的情况
def helper(a,b):
# 仅仅是子结构b == None的情况,
if b == None: return True
if a == None: return False
if a.val == b.val:
if helper(a.left,b.left) and helper(a.right,b.right): return True
if B == b:
if helper(a.left,b) or helper(a.right,b): return True
return False
return helper(A,B)
执行用时 :192 ms, 在所有 Python3 提交中击败了14.01%的用户
内存消耗 :18 MB, 在所有 Python3 提交中击败了100.00%的用户
# Definition for a binary tree node.
# class TreeNode:
# def __init__(self, x):
# self.val = x
# self.left = None
# self.right = None
class Solution:
def isSubStructure(self, A: TreeNode, B: TreeNode) -> bool:
def ismatch(A,B):
# 对比left和right
if A == None or A.val != B.val: return False
return (B.left == None or ismatch(A.left,B.left)) and (B.right == None or ismatch(A.right,B.right))
if A == None and B == None: return True
if A == None or B == None: return False
if A.val == B.val and ismatch(A,B):
return True
else:
return self.isSubStructure(A.right,B) or self.isSubStructure(A.left,B)
执行用时 :156 ms, 在所有 Python3 提交中击败了32.10%的用户
内存消耗 :17.7 MB, 在所有 Python3 提交中击败了100.00%的用户
[13]面试题32 - I. 从上到下打印二叉树【中等】
从上到下打印出二叉树的每个节点,同一层的节点按照从左到右的顺序打印。
例如:
给定二叉树: [3,9,20,null,null,15,7],
3
/
9 20
/
15 7
返回:
[3,9,20,15,7]
提示:
节点总数 <= 1000
# Definition for a binary tree node.
# class TreeNode:
# def __init__(self, x):
# self.val = x
# self.left = None
# self.right = None
from queue import Queue
class Solution:
def levelOrder(self, root: TreeNode) -> List[int]:
if root == None: return []
queue = Queue()
queue.put(root)
res = []
while queue.empty() == False:
node = queue.get() # get相当于列表中的pop
res.append(node.val)
if node.left:
queue.put(node.left) # 可能是棵树,也可能是个数
if node.right:
queue.put(node.right)
return res
本代码或者说本题的一个思路就是,将
Tree逐渐细分,[root,root.left,root.right,root.left.left,root.left.right, ... ],其中的每个元素是一棵树,如果将他这么细分下去,那么我们只需要得到每个元素(树)的val值,并将其插入列表就可实现本题的功能。
执行用时 :44 ms, 在所有 Python3 提交中击败了48.76%的用户
内存消耗 :13.8 MB, 在所有 Python3 提交中击败了100.00%的用户
[13附加题]面试题32 - III. 从上到下打印二叉树 III【中等】
请实现一个函数按照之字形顺序打印二叉树,即第一行按照从左到右的顺序打印,第二层按照从右到左的顺序打印,第三行再按照从左到右的顺序打印,其他行以此类推。
例如:
给定二叉树: [3,9,20,null,null,15,7],
3
/
9 20
/
15 7
返回其层次遍历结果:
[
[3],
[20,9],
[15,7]
]
提示:
节点总数 <= 1000
# Definition for a binary tree node.
# class TreeNode:
# def __init__(self, x):
# self.val = x
# self.left = None
# self.right = None
class Solution:
def levelOrder(self, root: TreeNode) -> List[List[int]]:
if not root: return []
reverseFlag = False
queue = [root]
res_lst = []
while queue:
nextQueue = []
# 由于nextQueue是要用来为下一次的遍历做准备,而且,同一层的节点在一个[]
# 因此要放入同一个循环中
valueQueue = []
for node in queue:
if not node:
continue
nextQueue.append(node.left)
nextQueue.append(node.right)
valueQueue.append(node.val)
queue = nextQueue
if reverseFlag:
valueQueue = valueQueue[::-1]
reverseFlag = not reverseFlag
if valueQueue:
res_lst.append(valueQueue)
return res_lst
[14] 面试题34. 二叉树中和为某一值的路径【中等】
输入一棵二叉树和一个整数,打印出二叉树中节点值的和为输入整数的所有路径。从树的根节点开始往下一直到叶节点所经过的节点形成一条路径。
示例:
给定如下二叉树,以及目标和 sum = 22,
5
/
4 8
/ /
11 13 4
/ /
7 2 5 1
返回:
[
[5,4,11,2],
[5,8,4,5]
]
提示:
节点总数 <= 10000
# Definition for a binary tree node.
# class TreeNode:
# def __init__(self, x):
# self.val = x
# self.left = None
# self.right = None
class Solution:
def pathSum(self, root: TreeNode, sum: int) -> List[List[int]]:
ans, path = [],[]
def dfs(root, sum):
if not root: return
path.append(root.val)
sum -= root.val
if not root.left and not root.right and not sum:
# not sum以为这在叶子结点处是否将sum减小至0
ans.append(path[:])
dfs(root.left, sum)
dfs(root.right, sum)
path.pop()
# 对于path,并非属于并行,递归他也有前后顺序的
# 按照例子,首先path中的元素为[5,4,11,7],之后由于sum不为0,未将path插入ans中
# 也就是在root=7的时候,dfs(root.left, sum) 和 dfs(root.right, sum)执行
# 并且什么都不返回,之后执行path.pop(),那么path就变成[5,4,11]
# 之后root退回到11,此时,root==1中dfs(root.left, sum)已经完成,开始执行
# dfs(root.right, sum),root.right == 2,同时递归到下一轮,path变为[5,4,11,2]
dfs(root, sum)
return ans
执行用时 :52 ms, 在所有 Python3 提交中击败了68.81%的用户
内存消耗 :15.1 MB, 在所有 Python3 提交中击败了100.00%的用户
[14附加题]124. 二叉树中的最大路径和【困难】
给定一个非空二叉树,返回其最大路径和。
本题中,路径被定义为一条从树中任意节点出发,达到任意节点的序列。该路径至少包含一个节点,且不一定经过根节点。
示例 1:
输入: [1,2,3]
1
/
2 3
输出: 6
示例 2:
输入: [-10,9,20,null,null,15,7]
-10
/
9 20
/
15 7
输出: 42
# Definition for a binary tree node.
# class TreeNode:
# def __init__(self, x):
# self.val = x
# self.left = None
# self.right = None
class Solution:
def dfs_sum(self, root: TreeNode):
# 一个分支
if root == None: return 0
val = root.val
sum_l = max(0, self.dfs_sum(root.left)) # 此处的0就是不把小于0的分支加进去
sum_r = max(0, self.dfs_sum(root.right))
self.ans = max(self.ans, sum_l + sum_r + val)
return max(sum_l , sum_r) + val
def maxPathSum(self, root: TreeNode) -> int:
self.ans = -1e9 # 防止只有一个元素且为负,self.ans代表的是遍历的树中的最大值
self.dfs_sum(root)
return self.ans
执行用时 :140 ms, 在所有 Python3 提交中击败了21.54%的用户
内存消耗 :20.2 MB, 在所有 Python3 提交中击败了51.79%的用户
[15] 98. 验证二叉搜索树【中等】
给定一个二叉树,判断其是否是一个有效的二叉搜索树。
假设一个二叉搜索树具有如下特征:
- 节点的左子树只包含小于当前节点的数。
- 节点的右子树只包含大于当前节点的数。
- 所有左子树和右子树自身必须也是二叉搜索树。
示例 1:
输入:
2
/
1 3
输出: true
示例 2:
输入:
5
/
1 4
/
3 6
输出: false
解释: 输入为: [5,1,4,null,null,3,6]。
根节点的值为 5 ,但是其右子节点值为 4 。
1 递归,中序遍历
# Definition for a binary tree node.
# class TreeNode:
# def __init__(self, x):
# self.val = x
# self.left = None
# self.right = None
class Solution:
def isValidBST(self, root: TreeNode) -> bool:
res = []
def helper(root):
if not root:
return
helper(root.left)
res.append(root.val)
helper(root.right)
helper(root)
return res == sorted(res) and len(set(res)) == len(res)
执行用时 :56 ms, 在所有 Python3 提交中击败了47.26%的用户
内存消耗 :17 MB, 在所有 Python3 提交中击败了5.10%的用户
2 最大值最小值
# Definition for a binary tree node.
# class TreeNode:
# def __init__(self, x):
# self.val = x
# self.left = None
# self.right = None
class Solution:
def isValidBST(self, root: TreeNode) -> bool:
def isBST(root, min_val, max_val):
if root == None:
return True
# print(root.val)
if root.val >= max_val or root.val <= min_val:
return False
return isBST(root.left, min_val, root.val) and isBST(root.right, root.val, max_val)
return isBST(root, float("-inf"), float("inf"))
[15附加题]面试题36. 二叉搜索树与双向链表【中等】
输入一棵二叉搜索树,将该二叉搜索树转换成一个排序的循环双向链表。要求不能创建任何新的节点,只能调整树中节点指针的指向。
为了让您更好地理解问题,以下面的二叉搜索树为例:
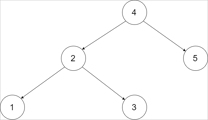
我们希望将这个二叉搜索树转化为双向循环链表。链表中的每个节点都有一个前驱和后继指针。对于双向循环链表,第一个节点的前驱是最后一个节点,最后一个节点的后继是第一个节点。
下图展示了上面的二叉搜索树转化成的链表。“head” 表示指向链表中有最小元素的节点。

特别地,我们希望可以就地完成转换操作。当转化完成以后,树中节点的左指针需要指向前驱,树中节点的右指针需要指向后继。还需要返回链表中的第一个节点的指针。
"""
# Definition for a Node.
class Node:
def __init__(self, val, left=None, right=None):
self.val = val
self.left = left
self.right = right
"""
class Solution:
def treeToDoublyList(self, root: 'Node') -> 'Node':
if root is None:
return None
self.first = None
self.last = None
self.helper(root)
self.first.left = self.last
self.last.right = self.first
return self.first
def helper(self, root):
# 此处的遍历方式为中序遍历,因此都是从小到大遍历的
# 也就是访问的前一个节点是后一个节点的left
# 有一个节点是前一个节点的right
if root is None:
return
self.helper(root.left)
if self.last is not None:
root.left = self.last
self.last.right = root # 虽然进行该操作,但都是对root的修改
else:
self.first = root # 只会发生一次
self.last = root
self.helper(root.right)
执行用时 :60 ms, 在所有 Python3 提交中击败了25.11%的用户
内存消耗 :14.5 MB, 在所有 Python3 提交中击败了100.00%的用户
[16]面试题54. 二叉搜索树的第k大节点【简单】
给定一棵二叉搜索树,请找出其中第k大的节点。
示例 1:
输入: root = [3,1,4,null,2], k = 1
3
/
1 4
2
输出: 4
示例 2:
输入: root = [5,3,6,2,4,null,null,1], k = 3
5
/
3 6
/
2 4
/
1
输出: 4
限制:
1 ≤ k ≤ 二叉搜索树元素个数
示例代码:
# Definition for a binary tree node.
# class TreeNode:
# def __init__(self, x):
# self.val = x
# self.left = None
# self.right = None
# 将二叉树中的每个元素放入列表,之后去其中第k大值
class Solution:
def kthLargest(self, root: TreeNode, k: int) -> int:
lst = []
def tree2list(root):
if not root : return
tree2list(root.left)
lst.append(root.val)
tree2list(root.right)
tree2list(root)
return lst[-k]
执行用时 :60 ms, 在所有 Python3 提交中击败了78.76%的用户
内存消耗 :17.5 MB, 在所有 Python3 提交中击败了100.00%的用户
[16附加题]98. 验证二叉搜索树
难度中等464
给定一个二叉树,判断其是否是一个有效的二叉搜索树。
假设一个二叉搜索树具有如下特征:
- 节点的左子树只包含小于当前节点的数。
- 节点的右子树只包含大于当前节点的数。
- 所有左子树和右子树自身必须也是二叉搜索树。
示例 1:
输入:
2
/
1 3
输出: true
示例 2:
输入:
5
/
1 4
/
3 6
输出: false
解释: 输入为: [5,1,4,null,null,3,6]。
根节点的值为 5 ,但是其右子节点值为 4 。
示例代码:
# Definition for a binary tree node.
# class TreeNode:
# def __init__(self, x):
# self.val = x
# self.left = None
# self.right = None
class Solution:
def isValidBST(self, root: TreeNode) -> bool:
lst = []
def tree2lst(root):
if not root: return
tree2lst(root.left)
lst.append(root.val)
tree2lst(root.right)
tree2lst(root)
return lst == sorted(lst) and len(set(lst)) == len(lst)
执行用时 :56 ms, 在所有 Python3 提交中击败了47.56%的用户
内存消耗 :16.9 MB, 在所有 Python3 提交中击败了5.00%的用户
[17]111. 二叉树的最小深度
难度简单229收藏分享切换为英文关注反馈
给定一个二叉树,找出其最小深度。
最小深度是从根节点到最近叶子节点的最短路径上的节点数量。
说明: 叶子节点是指没有子节点的节点。
示例:
给定二叉树 [3,9,20,null,null,15,7],
3
/
9 20
/
15 7
返回它的最小深度 2.
# Definition for a binary tree node.
# class TreeNode:
# def __init__(self, x):
# self.val = x
# self.left = None
# self.right = None
class Solution:
def minDepth(self, root: TreeNode) -> int:
if not root: return 0
l_depth = self.minDepth(root.left)
r_depth = self.minDepth(root.right)
return min(l_depth,r_depth) + 1 if (l_depth and r_depth) else 1+l_depth + r_depth
# 本题的关键就是,如果一个节点的左、右子树中只有一个存在,那么就用存在的那个,如果都没有就没有咯
执行用时 :84 ms, 在所有 Python3 提交中击败了8.42%的用户
内存消耗 :15.4 MB, 在所有 Python3 提交中击败了5.22%的用户
[17附加题]130. 被围绕的区域【中等】
给定一个二维的矩阵,包含 'X' 和 'O'(字母 O)。
找到所有被 'X' 围绕的区域,并将这些区域里所有的 'O' 用 'X' 填充。
示例:
X X X X
X O O X
X X O X
X O X X
运行你的函数后,矩阵变为:
X X X X
X X X X
X X X X
X O X X
解释:
被围绕的区间不会存在于边界上,换句话说,任何边界上的 'O' 都不会被填充为 'X'。 任何不在边界上,或不与边界上的 'O' 相连的 'O' 最终都会被填充为 'X'。如果两个元素在水平或垂直方向相邻,则称它们是“相连”的。
class Solution:
def solve(self, board: List[List[str]]) -> None:
"""
Do not return anything, modify board in-place instead.
"""
def dfs(board,i,j):
if i<0 or j<0 or i>=row_num or j >= column_num or board[i][j] == "X" or board[i][j] == "#":
return
board[i][j] = "#"
dfs(board, i - 1, j); # 上
dfs(board, i + 1, j); # 下
dfs(board, i, j - 1); # 左
dfs(board, i, j + 1); # 右
# 只要和最外侧的O相连,不论是直接相连,还是中间隔了个O,都算相连,要处理
# 那么,对于里面的,只要判断他就行了,没有必要看周围了
if board == None or len(board) == 0: return
row_num = len(board)
column_num = len(board[0])
for i in range(row_num):
for j in range(column_num):
isEdge = i == 0 or j == 0 or i == row_num - 1 or j == column_num - 1
if isEdge and board[i][j] == "O":
dfs(board,i,j)
for i in range(row_num):
for j in range(column_num):
if board[i][j] == "O":
board[i][j] = "X"
if board[i][j] == "#":
board[i][j] = "O"
执行用时 :84 ms, 在所有 Python3 提交中击败了78.10%的用户
内存消耗 :14.7 MB, 在所有 Python3 提交中击败了20.73%的用户
[18]200. 岛屿数量【中等】
给定一个由 '1'(陆地)和 '0'(水)组成的的二维网格,计算岛屿的数量。一个岛被水包围,并且它是通过水平方向或垂直方向上相邻的陆地连接而成的。你可以假设网格的四个边均被水包围。
示例 1:
输入:
11110
11010
11000
00000
输出: 1
示例 2:
输入:
11000
11000
00100
00011
输出: 3
class Solution:
def numIslands(self, grid: List[List[str]]) -> int:
# 对于该问题,我们可以这样考虑
# 通过递归,来依次寻扎周围的1
# 如果上、下、左、右都没有的时候,说明就是一个独立的岛
def count_island(grid,i,j):
if i < 0 or j <0 or i >= rows_num or j >= column_num or grid[i][j] == "0" or grid[i][j] == "2":
return
elif grid[i][j] == "1":
grid[i][j] = "2"
count_island(grid,i+1,j)
count_island(grid,i,j+1)
count_island(grid,i-1,j)
count_island(grid,i,j-1)
k = 0 # 岛的数量
if not grid or len(grid) == 0:return k
rows_num = len(grid)
column_num = len(grid[0])
for i in range(rows_num):
for j in range(column_num):
if grid[i][j] == "1":
count_island(grid,i,j)
k += 1
# 在遍历过程中,每遇到1,通过递归把这一类的1变成2
# 之后再进行同一类型1的下一个位置的遍历时,将不会在计算岛的个数
return k
执行用时 :72 ms, 在所有 Python3 提交中击败了95.01%的用户
内存消耗 :14.1 MB, 在所有 Python3 提交中击败了20.13%的用户
[18附加题]529. 扫雷游戏【中等】
让我们一起来玩扫雷游戏!
给定一个代表游戏板的二维字符矩阵。 'M' 代表一个未挖出的地雷,'E' 代表一个未挖出的空方块,'B' 代表没有相邻(上,下,左,右,和所有4个对角线)地雷的已挖出的空白方块,数字('1' 到 '8')表示有多少地雷与这块已挖出的方块相邻,'X' 则表示一个已挖出的地雷。
现在给出在所有未挖出的方块中('M'或者'E')的下一个点击位置(行和列索引),根据以下规则,返回相应位置被点击后对应的面板:
- 如果一个地雷('M')被挖出,游戏就结束了- 把它改为 'X'。
- 如果一个没有相邻地雷的空方块('E')被挖出,修改它为('B'),并且所有和其相邻的方块都应该被递归地揭露。
- 如果一个至少与一个地雷相邻的空方块('E')被挖出,修改它为数字('1'到'8'),表示相邻地雷的数量。
- 如果在此次点击中,若无更多方块可被揭露,则返回面板。
示例 1:
输入:
[['E', 'E', 'E', 'E', 'E'],
['E', 'E', 'M', 'E', 'E'],
['E', 'E', 'E', 'E', 'E'],
['E', 'E', 'E', 'E', 'E']]
Click : [3,0]
输出:
[['B', '1', 'E', '1', 'B'],
['B', '1', 'M', '1', 'B'],
['B', '1', '1', '1', 'B'],
['B', 'B', 'B', 'B', 'B']]
解释:

示例 2:
输入:
[['B', '1', 'E', '1', 'B'],
['B', '1', 'M', '1', 'B'],
['B', '1', '1', '1', 'B'],
['B', 'B', 'B', 'B', 'B']]
Click : [1,2]
输出:
[['B', '1', 'E', '1', 'B'],
['B', '1', 'X', '1', 'B'],
['B', '1', '1', '1', 'B'],
['B', 'B', 'B', 'B', 'B']]
解释:

注意:
- 输入矩阵的宽和高的范围为 [1,50]。
- 点击的位置只能是未被挖出的方块 ('M' 或者 'E'),这也意味着面板至少包含一个可点击的方块。
- 输入面板不会是游戏结束的状态(即有地雷已被挖出)。
- 简单起见,未提及的规则在这个问题中可被忽略。例如,当游戏结束时你不需要挖出所有地雷,考虑所有你可能赢得游戏或标记方块的情况。
class Solution:
def updateBoard(self, board: List[List[str]], click: List[int]) -> List[List[str]]:
def getnum(board,x,y):
num = 0
for i in range(-1,2):
for j in range(-1,2):
if x + i >= 0 and x + i < len(board) and y + j >=0 and y + j < len(board[0]) and board[x + i][y + j] == 'M':
num += 1
return num
def click_bar(board,x,y):
num = getnum(board,x,y)
if num == 0:
board[x][y] = "B"
for i in range(-1,2):
for j in range(-1,2):
if x + i >= 0 and x + i < len(board) and y + j >=0 and y + j < len(board[0]) and board[x + i][y + j] == 'E':
board = click_bar(board,x+i,y+j)
else:
board[x][y] = "{}".format(num)
return board
if board[click[0]][click[1]] == "M":
board[click[0]][click[1]] = "X"
return board
return click_bar(board,click[0],click[1])
执行用时 :356 ms, 在所有 Python3 提交中击败了9.52%的用户
内存消耗 :16.3 MB, 在所有 Python3 提交中击败了5.00%的用户
链表与二叉树的复习
[19]257. 二叉树的所有路径【简单】
给定一个二叉树,返回所有从根节点到叶子节点的路径。
说明: 叶子节点是指没有子节点的节点。
示例:
输入:
1
/
2 3
5
输出: ["1->2->5", "1->3"]
解释: 所有根节点到叶子节点的路径为: 1->2->5, 1->3
# Definition for a binary tree node.
# class TreeNode:
# def __init__(self, x):
# self.val = x
# self.left = None
# self.right = None
class Solution:
def binaryTreePaths(self, root: TreeNode) -> List[str]:
if not root:
return []
if not root.left and not root.right:
return [str(root.val)]
path = []
if root.left:
for i in self.binaryTreePaths(root.left):
path.append(str(root.val)+"->"+i)
if root.right:
for i in self.binaryTreePaths(root.right):
# self.binaryTreePaths(root.right)返回的是由其子树构成的列表
path.append(str(root.val)+"->"+i)
return path
"""
解题思路:
以例题中的例子为例,我们在构建递归算法时,先考虑最初的模型,之后再看看它能否推广至全部,
最重要的是,要终止条件的设定。
根据题意,每个节点,都需要进行分离,分为两个分支,存入列表中。
"1->i"self.binaryTreePaths(root.left)和"1->i"self.binaryTreePaths(root.right)
之后,右侧返回[3]
左侧返回["2->5"]或者["2->5","2->4"]
每个几点返回它与其两个子节点的拼接
"""
执行用时 :32 ms, 在所有 Python3 提交中击败了89.15%的用户
内存消耗 :13.5 MB, 在所有 Python3 提交中击败了5.24%的用户
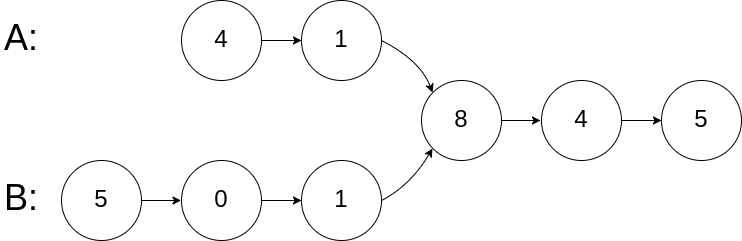
[19附加题]160. 相交链表【简单】
编写一个程序,找到两个单链表相交的起始节点。
如下面的两个链表:
在节点 c1 开始相交。
示例 1:
输入:intersectVal = 8, listA = [4,1,8,4,5], listB = [5,0,1,8,4,5], skipA = 2, skipB = 3
输出:Reference of the node with value = 8
输入解释:相交节点的值为 8 (注意,如果两个列表相交则不能为 0)。从各自的表头开始算起,链表 A 为 [4,1,8,4,5],链表 B 为 [5,0,1,8,4,5]。在 A 中,相交节点前有 2 个节点;在 B 中,相交节点前有 3 个节点。
示例 2:
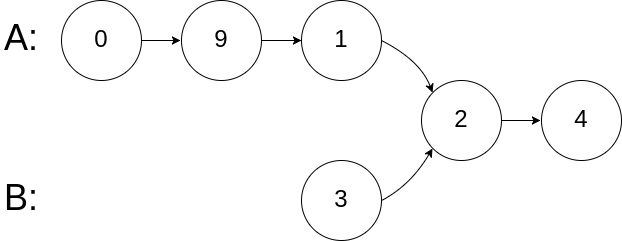
输入:intersectVal = 2, listA = [0,9,1,2,4], listB = [3,2,4], skipA = 3, skipB = 1
输出:Reference of the node with value = 2
输入解释:相交节点的值为 2 (注意,如果两个列表相交则不能为 0)。从各自的表头开始算起,链表 A 为 [0,9,1,2,4],链表 B 为 [3,2,4]。在 A 中,相交节点前有 3 个节点;在 B 中,相交节点前有 1 个节点。
示例 3:
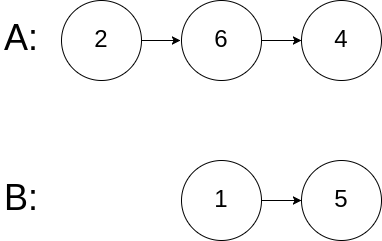
输入:intersectVal = 0, listA = [2,6,4], listB = [1,5], skipA = 3, skipB = 2
输出:null
输入解释:从各自的表头开始算起,链表 A 为 [2,6,4],链表 B 为 [1,5]。由于这两个链表不相交,所以 intersectVal 必须为 0,而 skipA 和 skipB 可以是任意值。
解释:这两个链表不相交,因此返回 null。
注意:
- 如果两个链表没有交点,返回
null. - 在返回结果后,两个链表仍须保持原有的结构。
- 可假定整个链表结构中没有循环。
- 程序尽量满足 O(n) 时间复杂度,且仅用 O(1) 内存。
# Definition for singly-linked list.
# class ListNode:
# def __init__(self, x):
# self.val = x
# self.next = None
"""
也就是说,仅仅是改变列表的结构
[0,9,1,2,4]
[3,2,4]
"""
class Solution:
def getIntersectionNode(self, headA: ListNode, headB: ListNode) -> ListNode:
if not headA or not headB: return None
pA, pB = headA, headB
# 因为两个链表,相同的部分在他们后面,所以不妨将对于给定的两个指针,
# 对两个链表都进行遍历,那么遍历的长度就相同了
while pA != pB:
if not pA:
pA = headB
else:
# 在这种情况下,不改变headA或headB的结构,也就是他们还是输入的那个值
pA = pA.next
if not pB:
pB = headA
else:
pB = pB.next
return pA
执行用时 :176 ms, 在所有 Python3 提交中击败了65.98%的用户
内存消耗 :29 MB, 在所有 Python3 提交中击败了5.44%的用户
[20]143. 重排链表【中等】难
给定一个单链表 L:L0→L1→…→L**n-1→Ln ,
将其重新排列后变为: L0→L**n→L1→L**n-1→L2→L**n-2→…
你不能只是单纯的改变节点内部的值,而是需要实际的进行节点交换。
示例 1:
给定链表 1->2->3->4, 重新排列为 1->4->2->3.
示例 2:
给定链表 1->2->3->4->5, 重新排列为 1->5->2->4->3.
# Definition for singly-linked list.
# class ListNode:
# def __init__(self, x):
# self.val = x
# self.next = None
class Solution:
def reorderList(self, head: ListNode) -> None:
"""
Do not return anything, modify head in-place instead.
"""
# [1,2,3,4]
if not head or not head.next: return head
p_first = head
p_last = head
while p_last.next and p_last.next.next:
# 不改变原有的链表结构
p_last = p_last.next.next
p_first = p_first.next
p = p_first.next
# 相当于把后半部分给了p,此时,p已经与head无关
right = None
# 由于p_first指向的是head,因此,经过下面操作,head 为 [1,2]
p_first.next = None # 改变了原有的链表
while p:
# 就好像啊a,b = b,a,右侧的a,b是根据前文所给的a,b值得到的
# 也就是说,a,b = b,a和b,a = a,b的效果是一样的,它俩没有前后关系
# 如果在一个循环中,本轮的a,b值是由上一轮的a,b值确定
# 如果是多个值,如c,b,a=a,c,b,本轮中,左侧可以继承左侧的值,此时,开始有运算的先后顺序
# 这几个操作与head无关,仅仅是基于p的,p为[3,4]
# 第一轮right为[3],第二轮为[4,3]
right,right.next,p = p,right,p.next
# left为[1,2]
left = head
while left and right:
# left [1,4,3],right [4,2],left [2],right [3]
# left [1,4,2],right
left.next,right.next,left,right = right,left.next,left.next,right.next
执行用时 :92 ms, 在所有 Python3 提交中击败了73.25%的用户
内存消耗 :22.2 MB, 在所有 Python3 提交中击败了10.65%的用户
[20附加题]508. 出现次数最多的子树元素和【中等】
给出二叉树的根,找出出现次数最多的子树元素和。一个结点的子树元素和定义为以该结点为根的二叉树上所有结点的元素之和(包括结点本身)。然后求出出现次数最多的子树元素和。如果有多个元素出现的次数相同,返回所有出现次数最多的元素(不限顺序)。
示例 1
输入:
5
/
2 -3
返回 [2, -3, 4],所有的值均只出现一次,以任意顺序返回所有值。
示例 2
输入:
5
/
2 -5
返回 [2],只有 2 出现两次,-5 只出现 1 次。
提示: 假设任意子树元素和均可以用 32 位有符号整数表示。
# Definition for a binary tree node.
# class TreeNode:
# def __init__(self, x):
# self.val = x
# self.left = None
# self.right = None
# import numpy as np
class Solution:
def findFrequentTreeSum(self, root: TreeNode) -> List[int]:
if not root: return []
sum_lst = []
def sum_tree(root):
if not root: return 0
left = sum_tree(root.left)
right = sum_tree(root.right)
sum_child_tree = root.val + left + right
sum_lst.append(sum_child_tree)
return sum_child_tree
sum_tree(root)
dict_tree = dict()
for i in sum_lst:
if i not in dict_tree:
dict_tree[i] = 1
else:
dict_tree[i] += 1
# print(dict_tree)
max_num = max(list(dict_tree.values()))
lst = []
for i in dict_tree.keys():
if dict_tree[i] == max_num:
lst.append(i)
return sorted(lst)
执行用时 :64 ms, 在所有 Python3 提交中击败了47.74%的用户
内存消耗 :17.1 MB, 在所有 Python3 提交中击败了5.13%的用户
[21]337. 打家劫舍 III【中等】
在上次打劫完一条街道之后和一圈房屋后,小偷又发现了一个新的可行窃的地区。这个地区只有一个入口,我们称之为“根”。 除了“根”之外,每栋房子有且只有一个“父“房子与之相连。一番侦察之后,聪明的小偷意识到“这个地方的所有房屋的排列类似于一棵二叉树”。 如果两个直接相连的房子在同一天晚上被打劫,房屋将自动报警。
计算在不触动警报的情况下,小偷一晚能够盗取的最高金额。
示例 1:
输入: [3,2,3,null,3,null,1]
3
/
2 3
3 1
输出: 7
解释: 小偷一晚能够盗取的最高金额 = 3 + 3 + 1 = 7.
示例 2:
输入: [3,4,5,1,3,null,1]
3
/
4 5
/
1 3 1
输出: 9
解释: 小偷一晚能够盗取的最高金额 = 4 + 5 = 9.
# Definition for a binary tree node.
# class TreeNode:
# def __init__(self, x):
# self.val = x
# self.left = None
# self.right = None
class Solution:
def dp(self , cur : TreeNode) -> List[int] :
if not cur :
return [0,0]
l = self.dp(cur.left)
r = self.dp(cur.right)
return [max(l)+max(r),cur.val+l[0]+r[0]]
# 左值是选择子树的叶子结点,但是不选择根节点,右值是选择根节点不选择叶子结点
# 通常第一眼想到的是return [l[1]+r[1],cur.val+l[0]+r[0]]
# 但是,左右子树可以是不一样的,在选择该节点的情况下,左右子树都不选,在不选择的情况下,对于左右子树
# 我们就要选择出其中的最大值,不管他是否选择该节点的叶子结点
# 不要把自己陷入一个误区,我们必须保证隔着不少于一个节点,但是也可以是两个
def rob(self, root: TreeNode) -> int:
return max(self.dp(root))
执行用时 :56 ms, 在所有 Python3 提交中击败了76.81%的用户
内存消耗 :15.7 MB, 在所有 Python3 提交中击败了14.16%的用户
[21附加题]147. 对链表进行插入排序【中等】难
对链表进行插入排序。

插入排序的动画演示如上。从第一个元素开始,该链表可以被认为已经部分排序(用黑色表示)。
每次迭代时,从输入数据中移除一个元素(用红色表示),并原地将其插入到已排好序的链表中。
插入排序算法:
- 插入排序是迭代的,每次只移动一个元素,直到所有元素可以形成一个有序的输出列表。
- 每次迭代中,插入排序只从输入数据中移除一个待排序的元素,找到它在序列中适当的位置,并将其插入。
- 重复直到所有输入数据插入完为止。
示例 1:
输入: 4->2->1->3
输出: 1->2->3->4
示例 2:
输入: -1->5->3->4->0
输出: -1->0->3->4->5
# Definition for singly-linked list.
# class ListNode:
# def __init__(self, x):
# self.val = x
# self.next = None
class Solution:
def insertionSortList(self, head: ListNode) -> ListNode:
# 找个排头
dummy = ListNode(float("-inf"))
pre = dummy
tail = dummy
# 依次拿head节点
cur = head
while cur:
if tail.val < cur.val:
tail.next = cur
tail = cur
cur = cur.next
else:
# 把下一次节点保持下来
tmp = cur.next
tail.next = tmp
# 找到插入的位置
while pre.next and pre.next.val < cur.val:
pre = pre.next
# 进行插入操作
cur.next = pre.next
pre.next = cur
pre= dummy
cur = tmp
return dummy.next
执行用时 :408 ms, 在所有 Python3 提交中击败了52.98%的用户
内存消耗 :15.4 MB, 在所有 Python3 提交中击败了6.39%的用户
[22]994. 腐烂的橘子【简单】
在给定的网格中,每个单元格可以有以下三个值之一:
- 值
0代表空单元格; - 值
1代表新鲜橘子; - 值
2代表腐烂的橘子。
每分钟,任何与腐烂的橘子(在 4 个正方向上)相邻的新鲜橘子都会腐烂。
返回直到单元格中没有新鲜橘子为止所必须经过的最小分钟数。如果不可能,返回 -1。
示例 1:
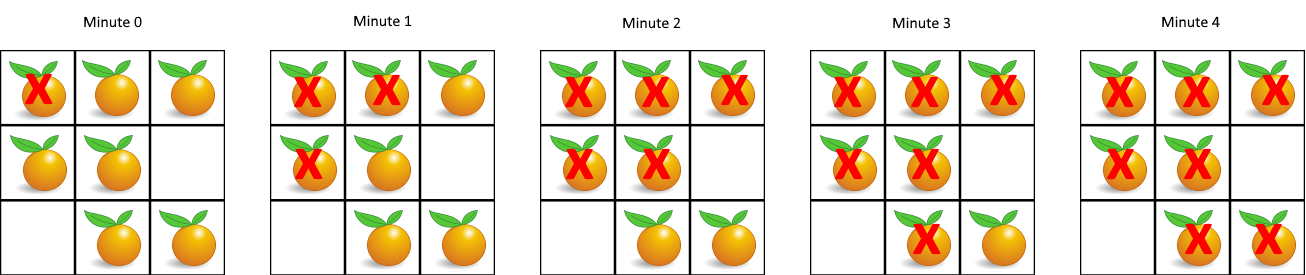
输入:[[2,1,1],[1,1,0],[0,1,1]]
输出:4
示例 2:
输入:[[2,1,1],[0,1,1],[1,0,1]]
输出:-1
解释:左下角的橘子(第 2 行, 第 0 列)永远不会腐烂,因为腐烂只会发生在 4 个正向上。
示例 3:
输入:[[0,2]]
输出:0
解释:因为 0 分钟时已经没有新鲜橘子了,所以答案就是 0 。
提示:
1 <= grid.length <= 101 <= grid[0].length <= 10grid[i][j]仅为0、1或2
[23]199. 二叉树的右视图【中等】
给定一棵二叉树,想象自己站在它的右侧,按照从顶部到底部的顺序,返回从右侧所能看到的节点值。
示例:
输入: [1,2,3,null,5,null,4]
输出: [1, 3, 4]
解释:
1 <---
/
2 3 <---
5 4 <---
[23附加题]112. 路径总和【简单】
给定一个二叉树和一个目标和,判断该树中是否存在根节点到叶子节点的路径,这条路径上所有节点值相加等于目标和。
说明: 叶子节点是指没有子节点的节点。
示例:
给定如下二叉树,以及目标和 sum = 22,
5
/
4 8
/ /
11 13 4
/
7 2 1
返回 true, 因为存在目标和为 22 的根节点到叶子节点的路径 5->4->11->2。
[24 ]543. 二叉树的直径【简单】
给定一棵二叉树,你需要计算它的直径长度。一棵二叉树的直径长度是任意两个结点路径长度中的最大值。这条路径可能穿过也可能不穿过根结点。
示例 :
给定二叉树
1
/
2 3
/
4 5
返回 3, 它的长度是路径 [4,2,1,3] 或者 [5,2,1,3]。
[24附加题]445. 两数相加 II[中等]
给定两个非空链表来代表两个非负整数。数字最高位位于链表开始位置。它们的每个节点只存储单个数字。将这两数相加会返回一个新的链表。
你可以假设除了数字 0 之外,这两个数字都不会以零开头。
进阶:
如果输入链表不能修改该如何处理?换句话说,你不能对列表中的节点进行翻转。
示例:
输入: (7 -> 2 -> 4 -> 3) + (5 -> 6 -> 4)
输出: 7 -> 8 -> 0 -> 7
停止刷题,搞一搞理论,再回来干
[25]103. 二叉树的锯齿形层次遍历【中等】
给定一个二叉树,返回其节点值的锯齿形层次遍历。(即先从左往右,再从右往左进行下一层遍历,以此类推,层与层之间交替进行)。
例如:
给定二叉树 [3,9,20,null,null,15,7],
3
/
9 20
/
15 7
返回锯齿形层次遍历如下:
[
[3],
[20,9],
[15,7]
]
[25附加题]面试题 02.06. 回文链表[简单]
编写一个函数,检查输入的链表是否是回文的。
示例 1:
输入: 1->2
输出: false
示例 2:
输入: 1->2->2->1
输出: true
进阶:
你能否用 O(n) 时间复杂度和 O(1) 空间复杂度解决此题?
[26]654. 最大二叉树【中等】
给定一个不含重复元素的整数数组。一个以此数组构建的最大二叉树定义如下:
- 二叉树的根是数组中的最大元素。
- 左子树是通过数组中最大值左边部分构造出的最大二叉树。
- 右子树是通过数组中最大值右边部分构造出的最大二叉树。
通过给定的数组构建最大二叉树,并且输出这个树的根节点。
示例 :
输入:[3,2,1,6,0,5]
输出:返回下面这棵树的根节点:
6
/
3 5
/
2 0
1
提示:
- 给定的数组的大小在 [1, 1000] 之间。
[26附加题]1019. 链表中的下一个更大节点【中等】
给出一个以头节点 head 作为第一个节点的链表。链表中的节点分别编号为:node_1, node_2, node_3, ... 。
每个节点都可能有下一个更大值(next larger value):对于 node_i,如果其 next_larger(node_i) 是 node_j.val,那么就有 j > i 且 node_j.val > node_i.val,而 j 是可能的选项中最小的那个。如果不存在这样的 j,那么下一个更大值为 0 。
返回整数答案数组 answer,其中 answer[i] = next_larger(node_{i+1}) 。
注意:*在下面的示例中,诸如 [2,1,5] 这样的输入*(不是输出)是链表的序列化表示,其头节点的值为 2,第二个节点值为 1,第三个节点值为 5 。
[27]100. 相同的树【简单】
给定两个二叉树,编写一个函数来检验它们是否相同。
如果两个树在结构上相同,并且节点具有相同的值,则认为它们是相同的。
示例 1:
输入: 1 1
/ /
2 3 2 3
[1,2,3], [1,2,3]
输出: true
示例 2:
输入: 1 1
/
2 2
[1,2], [1,null,2]
输出: false
示例 3:
输入: 1 1
/ /
2 1 1 2
[1,2,1], [1,1,2]
输出: false
[27 附加题]1290. 二进制链表转整数[简单]
给你一个单链表的引用结点 head。链表中每个结点的值不是 0 就是 1。已知此链表是一个整数数字的二进制表示形式。
请你返回该链表所表示数字的 十进制值 。
示例 1:
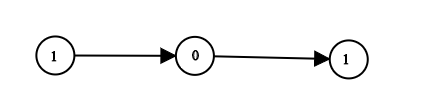
输入:head = [1,0,1]
输出:5
解释:二进制数 (101) 转化为十进制数 (5)
示例 2:
输入:head = [0]
输出:0
示例 3:
输入:head = [1]
输出:1
示例 4:
输入:head = [1,0,0,1,0,0,1,1,1,0,0,0,0,0,0]
输出:18880
示例 5:
输入:head = [0,0]
输出:0
提示:
- 链表不为空。
- 链表的结点总数不超过
30。 - 每个结点的值不是
0就是1。
[28]面试题10- II. 青蛙跳台阶问题【简单】
一只青蛙一次可以跳上1级台阶,也可以跳上2级台阶。求该青蛙跳上一个n 级的台阶总共有多少种跳法。
答案需要取模 1e9+7(1000000007),如计算初始结果为:1000000008,请返回 1。
示例 1:
输入:n = 2
输出:2
示例 2:
输入:n = 7
输出:21
提示:
0 <= n <= 100
注意:本题与主站 70 题相同:https://leetcode-cn.com/problems/climbing-stairs/
[28附加题]面试题 08.01. 三步问题【简单】
三步问题。有个小孩正在上楼梯,楼梯有n阶台阶,小孩一次可以上1阶、2阶或3阶。实现一种方法,计算小孩有多少种上楼梯的方式。结果可能很大,你需要对结果模1000000007。
示例1:
输入:n = 3
输出:4
说明: 有四种走法
示例2:
输入:n = 5
输出:13
提示:
- n范围在[1, 1000000]之间
[29]144. 二叉树的前序遍历【中等】
给定一个二叉树,返回它的 前序 遍历。
示例:
输入: [1,null,2,3]
1
2
/
3
输出: [1,2,3]
进阶: 递归算法很简单,你可以通过迭代算法完成吗?
[29a附加题]面试题 08.05. 递归乘法【中等】
递归乘法。 写一个递归函数,不使用 * 运算符, 实现两个正整数的相乘。可以使用加号、减号、位移,但要吝啬一些。
示例1:
输入:A = 1, B = 10
输出:10
示例2:
输入:A = 3, B = 4
输出:12
提示:
- 保证乘法范围不会溢出
[30]122. 买卖股票的最佳时机 II【简单】
给定一个数组,它的第 i 个元素是一支给定股票第 i 天的价格。
设计一个算法来计算你所能获取的最大利润。你可以尽可能地完成更多的交易(多次买卖一支股票)。
注意:你不能同时参与多笔交易(你必须在再次购买前出售掉之前的股票)。
示例 1:
输入: [7,1,5,3,6,4]
输出: 7
解释: 在第 2 天(股票价格 = 1)的时候买入,在第 3 天(股票价格 = 5)的时候卖出, 这笔交易所能获得利润 = 5-1 = 4 。
随后,在第 4 天(股票价格 = 3)的时候买入,在第 5 天(股票价格 = 6)的时候卖出, 这笔交易所能获得利润 = 6-3 = 3 。
示例 2:
输入: [1,2,3,4,5]
输出: 4
解释: 在第 1 天(股票价格 = 1)的时候买入,在第 5 天 (股票价格 = 5)的时候卖出, 这笔交易所能获得利润 = 5-1 = 4 。
注意你不能在第 1 天和第 2 天接连购买股票,之后再将它们卖出。
因为这样属于同时参与了多笔交易,你必须在再次购买前出售掉之前的股票。
示例 3:
输入: [7,6,4,3,1]
输出: 0
解释: 在这种情况下, 没有交易完成, 所以最大利润为 0。
class Solution:
def maxProfit(self, prices: List[int]) -> int:
# 遍历一遍,只要后一个比前一个大,就计算其差值
# 这样称为贪心算法,
# 如,第一天买入,第二天比第一天高,卖出
# 如果第三天比第二天高,继续卖出,这样第二天与第三天的差值 加上 第一天与第二天的差值,我们卖出了个高价钱
# 继续,如果第三天比第二天低,不求差值,也是明智的做法,第四天比第三天高,求差值
# 无论第四天比第二天高还是低,我们都得到了最多的钱
price_len = len(prices)
sum_num = 0
for i in range(price_len-1):
if prices[i] < prices[i+1]:
sum_num += prices[i+1]-prices[i]
return sum_num
执行用时 :40 ms, 在所有 Python3 提交中击败了91.80%的用户
内存消耗 :14.6 MB, 在所有 Python3 提交中击败了6.38%的用户
如下图所示,如果股票一路飙升,我们第一天买最后一天卖,得到的是图中最高点与最低点的最大差值;如果按照"红红黄红",相比于之前的最大差值,用红2-红1、红4-黄3这样的差值更大,”红红黄黄“也一样。
class Solution:
def maxProfit(self, prices: List[int]) -> int:
dp_i0 = 0
dp_i1 = float("-inf")
for i in prices:
dp_i0 = max(dp_i0,dp_i1+i)
dp_i1 = max(dp_i1,dp_i0 - i)
return dp_i0
[30附加题]123. 买卖股票的最佳时机 III[困难]
给定一个数组,它的第 i 个元素是一支给定的股票在第 i 天的价格。
设计一个算法来计算你所能获取的最大利润。你最多可以完成 两笔 交易。
注意: 你不能同时参与多笔交易(你必须在再次购买前出售掉之前的股票)。
示例 1:
输入: [3,3,5,0,0,3,1,4]
输出: 6
解释: 在第 4 天(股票价格 = 0)的时候买入,在第 6 天(股票价格 = 3)的时候卖出,这笔交易所能获得利润 = 3-0 = 3 。
随后,在第 7 天(股票价格 = 1)的时候买入,在第 8 天 (股票价格 = 4)的时候卖出,这笔交易所能获得利润 = 4-1 = 3 。
示例 2:
输入: [1,2,3,4,5]
输出: 4
解释: 在第 1 天(股票价格 = 1)的时候买入,在第 5 天 (股票价格 = 5)的时候卖出, 这笔交易所能获得利润 = 5-1 = 4 。
注意你不能在第 1 天和第 2 天接连购买股票,之后再将它们卖出。
因为这样属于同时参与了多笔交易,你必须在再次购买前出售掉之前的股票。
示例 3:
输入: [7,6,4,3,1]
输出: 0
解释: 在这个情况下, 没有交易完成, 所以最大利润为 0。
class Solution:
def maxProfit(self, prices: List[int]) -> int:
dp_i10 = 0
dp_i11 = float("-inf")
dp_i20 = 0
dp_i21 = float("-inf")
for i in prices:
dp_i10 = max(dp_i10, dp_i11 + i )
dp_i11 = max(dp_i11,-i)
dp_i20 = max(dp_i20,dp_i21+i)
dp_i21 = max(dp_i21,dp_i10-i)
return dp_i20
执行用时 :56 ms, 在所有 Python3 提交中击败了96.45%的用户
内存消耗 :14.5 MB, 在所有 Python3 提交中击败了45.83%的用户