论文笔记《Notes on convolutional neural networks》

这是个06年的老文章了，但是很多地方还是值得看一看的.

一、概要

  主要讲了CNN的Feedforward Pass和 Backpropagation Pass，关键是卷积层和polling层的BP推导讲解。

二、经典BP算法

 前向传播需要注意的是数据归一化，对训练数据进行归一化到 0 均值和单位方差，可以在梯度下降上改善，因为这样可以防止过早的饱，这主要还是因为早期的sigmoid和tanh作为激活函数的弊端（函数在过大或者过小的时候，梯度都很小），等现在有了RELU和batch normalization这两个神器，基本上对梯度消失的问题有了不错的解决。然后是BP算法，论文里面稍微难理解的是公式5的推导，

（引用的这里的翻译http://www.cnblogs.com/shouhuxianjian/p/4529202.html）：

 网络中我们需要后向传播的“ 误差”可以被认为是关于有偏置项扰动的每个单元的 “敏感性”。也就是说：

 

（公式4）

 

因为，所以偏置的敏感性其实等于一个单元的所有输入产生的误差偏导。下面的就是从高层到低层的BP：

 

（公式5）

因为左边是输入X的误差偏导，有因为，所以要前面的误差偏导乘上第l+1个W在乘上激活函数的偏导，这个如果对BP算法有所了解的话应该很好理解。

 

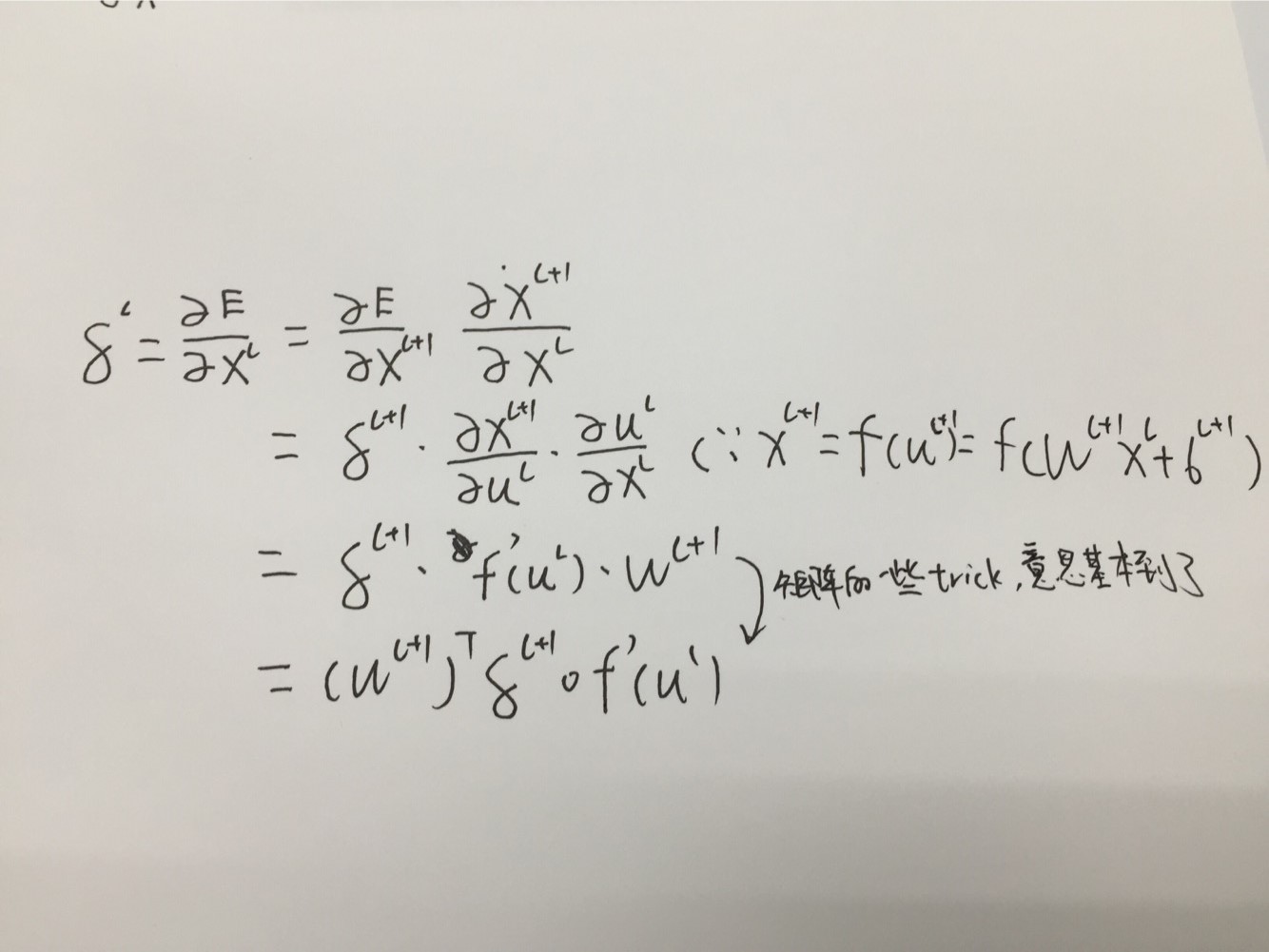
这里的“o” 表示是 逐原始相乘的。对于公式2中的误差函数，输出层神经元的敏感性如下：

 

（公式6） 

 

最后，关于某个给定的神经元的更新权重的delta-rule就是对那个神经元的输入部分进行复制，只是用神经元的delta进行缩放罢了（其实就是如下面公式7的两个相乘而已）。在向量的形式中，这相当于输入向量（前层的输出）和敏感性向量的外积：

 

（公式7）

 

（公式8）

 

 

 三、CNN

      Sub-sampling的好处是来减少计算时间并且逐步的建立更深远的空间和构型的不变性，后面一点说的很拗口，我的理解还是对平移和缩放不变性的confidence吧。

  1.计算梯度

    这里论文就很不讲道理了，直接摆公式，什么都没有...卷积层和polling层的反向传播还是相当重要的，这里推荐一篇博文http://www.cnblogs.com/tornadomeet/p/3468450.html，里面对CNN的BP算法讲的很好，基本上推完这四个问题，CNN的BP算法就有了一定的了解了

博客里面比较难理解的是这个图：

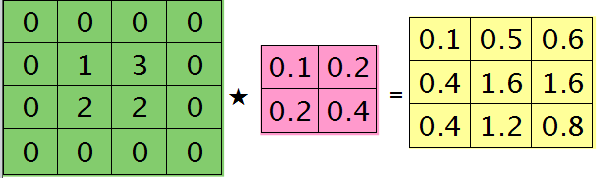
也就是把卷积核旋转180度以后，从做左到右，再从上到下，计算得到每个值，跟feadforward pass的卷积不同，因为那个其实是一个相关的操作...只不过以卷积的形式表现了出来，这个才是正统的卷积处理。

这里需要理清一下这四个问题，首先是输出的误差敏感项，这个直接看推导就行了，然后是卷积层的下一层为pooling层时，求卷积层的误差敏感项，因为反向传播的时候，输出会比输入小，所以梯度在传递的时候和传统BP算法不一样，所以如何得到卷积层的误差敏感项就是这个问题考虑的。第三个问题考虑的是pooling层下面接卷积层，这个是因为我们要得到pooling层的误差敏感性，依靠的是卷积核的误差敏感项求的，同样是因为scale 的问题，所以需要去考虑。最后一个问题就是卷积层本身，在得到输出的误差敏感性之后，怎么得到W的，这个只要用相关的操作就可以得到，简单的理解是l层i和l+1层j之间的权值等于l+1层j处误差敏感值乘以l层i处的输入，而卷积的操作是一个累加的过程，所以BP的时候，也需要相关的操作得到。

 四、combine

论文最后讲的几个feature map融合的想法也很好的理解，我的问题是，这个feature map不是一直作为多通道输出的么，为什么需要去融合，后来很多知名的net好像也并没有用到这个方法，是不是只是一次尝试？