例如:2^3。
首先将2转为二进制 01
3转为二进制 11
它们进行比较:
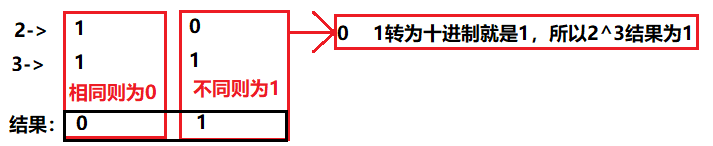
所以2^3=1
备注:如果相同的数计算抑或,则为0
有一道关于抑或的题:

原来我是这么写的:
1 /*O(n²)*/ 2 public int singleNumber1(int[] nums) { 3 for (int i = 0; i < nums.length; i++) { 4 // 是否重复 5 boolean flag = false; 6 for (int j = 0; j < nums.length; j++) { 7 if (i == j) { 8 continue; 9 } 10 if (nums[i] == nums[j]) { 11 flag = true; 12 break; 13 } 14 } 15 if (!flag) { 16 return nums[i]; 17 } 18 } 19 return -1; 20 }
但是后面发现很多人都用异或,异或中可以发现一个规律:
1 System.out.println(4 ^ 1 ^ 2 ^ 2 ^ 1);// 4 2 System.out.println(3 ^ 1 ^ 2 ^ 2 ^ 1);// 3 3 System.out.println(1 ^ 2 ^ 2 ^ 1 ^ 5);// 5 4 System.out.println(1 ^ 2 ^ 2 ^ 1 ^ 8);// 8
如果运算中,满足这个规则,A^B^B,那么结果一定是没有成对出现的A,然后回看那道题。
找出单独存在的元素,除开这个单独的元素,其他的元素都是成对出现的,所以可以使用异或来操作,代码如下:
1 public int singleNumber2(int[] nums) { 2 int result = 0; 3 for (int i = 0; i < nums.length; i++) { 4 result ^= nums[i]; 5 } 6 return result; 7 }