算法中：算法复杂度

算法复杂度

记录所用，如有内容有误请谨慎。

目录：

　　　1、简介

　　　2、时间频度

　　　3、时间复杂度

　　　　3-1、简介

　　　　3-2、常数阶 O(1)

　　　　3-3、对数阶 O(log₂n)

　　　　3-4、线性阶 O(n)

　　　　3-5、线性对数阶 O(nlog₂n)

　　　　3-6、平方阶 O(n²)

　　　　3-7、立方阶 O(n³)

　　　　3-8、k次方阶 O(n^k)

　　　　3-9、指数阶 O(2ⁿ)

　　　 4、平均时间复杂度和最坏时间复杂度

　　　 5、空间复杂度

1、简介

我们的一个算法如何来判断它的好坏，我们一般有两种方法：

第一种：事后统计法

　　这种方式就是在算法开始执行以前记录开始时间，然后算法执行结束以后记录结束时间，用结束时间-开始时间就是这个算法运行花费的时间。

　　但是这种方法会受到计算机硬件、软件的影响，比如同一个算法，在不同配置不同环境的电脑上运行效果是不一样的。

第二种：事前统计法

 　　这种方式就是通过时间复杂度来判断一个算法的好坏，而时间复杂度呢就是用特殊的符号特殊的规则来记录这个算法耗时的大致情况。

2、时间频度

 一个算法中语句执行次数称之为时间频度或者时间频度，记作T(n)。

来举例1+2+3+...+n：

  public static int sum1(int n) {
        int total = 0;
        for (int i = 1; i <= n; i++) {
            total += i;
        }
        return total;
    }

    public static int sum2(int n) {
        return (1 + n) * (n / 2);
    }

当我们n为100的时候，

　　sum1要循环一百次，加上上面的一句代码，那么sum1的时间频度就为：T(n)=n+1

　　sum2只需要执行一句代码，那么sum2的时间频度就为：T(n)=1

然后我们的平时在计算事件时间频度的时候，是可以忽略某些项的，就比如上方的sum1，n为100那么时间频度就为101，n为200，时间频度就为201，那么这个时候这个1可有可无，所以就可以被忽略。

下面列举常见的忽略各种项的情况：

1、忽略常数项：

 

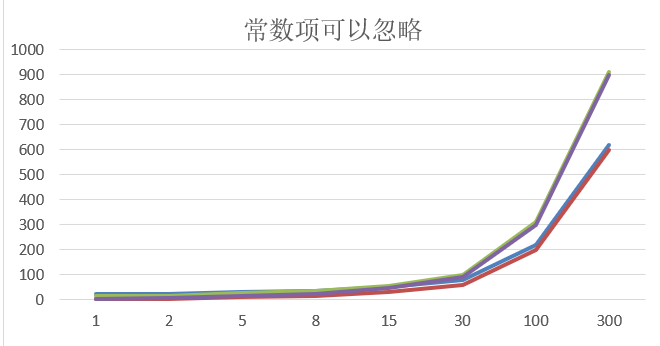
看这俩图，可以得出结论如下结论：

　　1、2n+20和2*n这两个之间，随着n变大，结果几乎没有被20所影响，所以20可以忽略，注:(在算式中普通的数字叫做常数项)

　　2、3n+10和3n这两个之间，随着n变大，也几乎没有被10所影响，所以10可以被忽略。

 2、忽略低次项

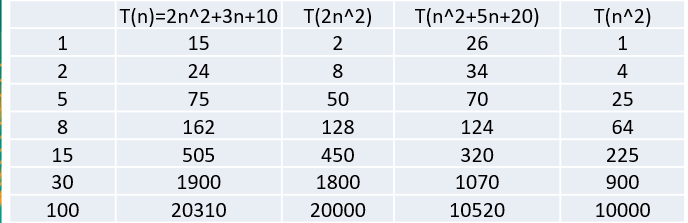
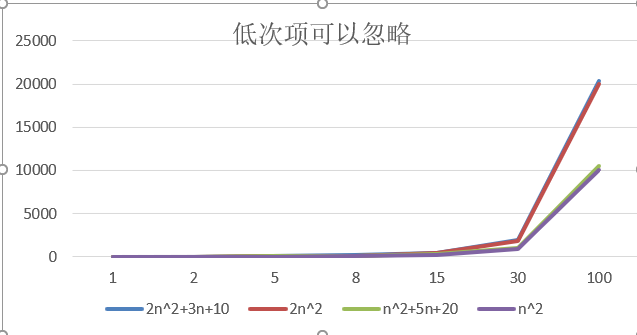
 得出结论：

　　1、2n²+3n+10和2n²这两个，随着n变大，结果几乎没有被3n+10影响，所以3n+10可以被忽略。

　　2、n²+5n+20和n²之间，随着n变大，5n+20也是几乎没影响，所以可以忽略

 3、忽略系数

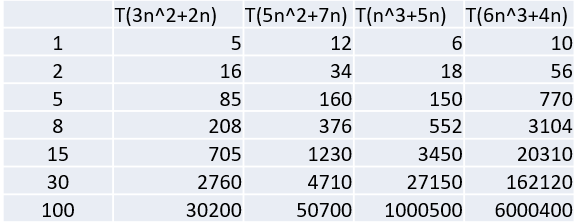
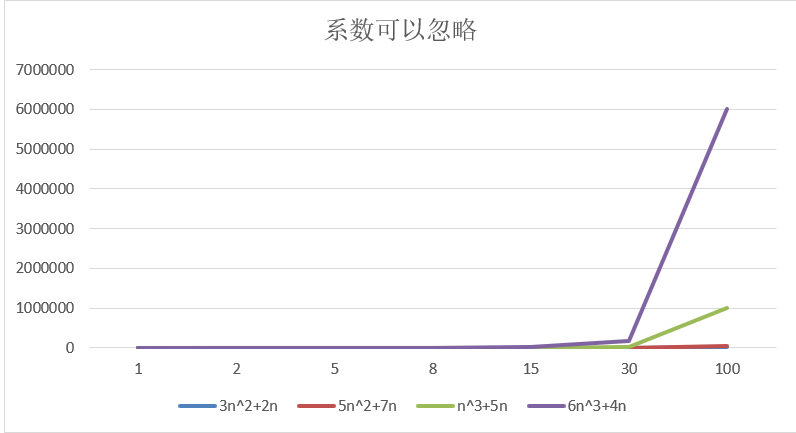
 得出结论：

　　1、3n²+2n和5n²+7n这两个，随着n变大，²的影响越来越小，所以²可以被忽略。

3、时间复杂度

3-1、简介 

 就是用特定的符号来讲一个算法的运行时间来代表起来。

 下面举例常见的复杂度。

 备注一下下面时间复杂度的效率：O(1)>O(log₂n)>O(n)>O(nlog₂n)>O(n²)>O(n³)>O(nk)>O(2n)

3-2、常数阶 O(1) 

public static int method1(int i) {
        int j = 2;
        i++;
        j++;
        return i + j;
    }

像这个代码，不论i为多少，代码永远都是执行那几次，里面没有循环等复杂操作，所以该算法的时间复杂度就是O(1)

3-3、对数阶 O(log₂n) 

public static void method1(int n) {
        int i = 1;
        while (i < n) {
            i = i * 2;
        }
    }

 看这个，当n为8的时候，运行3次，那么相当于是2³，那么就是8=2³，那么使用数学中对数的写法就是：3=log₂⁸

 那么我们将8换成n就是：运行次数=log₂ⁿ

 所以这个算法的时间复杂度就为O(log₂ⁿ)

3-4、线性阶 O(n) 

    public static void method1(int n) {
        for (int i = 1; i <= n; i++) {
            System.out.println("运行第:" + i);
        }
    }

这里，n为10，则for运行10次，那么这种情况的时间复杂度就为O(n)

3-5、线性对数阶 O(nlog₂n) 

    public static void method1(int n) {
        for (int i = 0; i <= n; i++) {
            int m = 1;
            while (m < n) {
                i = i * 2;
            }
        }
    }

这个咋看呢，外层的循环复杂度为O(n),里面的while复杂度为O(log₂ⁿ),然后如果n为10，那么这个算法的复杂°就为:O(10log₂¹⁰),所以这个算法的时间复杂度就是O(nlog₂ⁿ)。

3-6、平方阶 O(n²) 

public static void method1(int n) {
        for (int i = 0; i <= n; i++) {
            for (int j = 0; j <= n; i++) {
                System.out.println("haha");
            }
        }
    }

像这种，双层循环，内部是O(n),内部执行n次，那么复杂度就是O(n²) 

3-7、立方阶 O(n³) 

 就是在平方阶的基础上再套一层

3-8、k次方阶 O(n^k) 

 和立方阶/平方阶一样的道理。

3-9、指数阶 O(2ⁿ) 

 这个没找到案例

4、平均时间复杂度和最坏时间复杂度

 平均复杂度就是这个算法正常情况下的复杂度，最坏复杂度就是这个算法运行最坏的情况的复杂度。

如图：

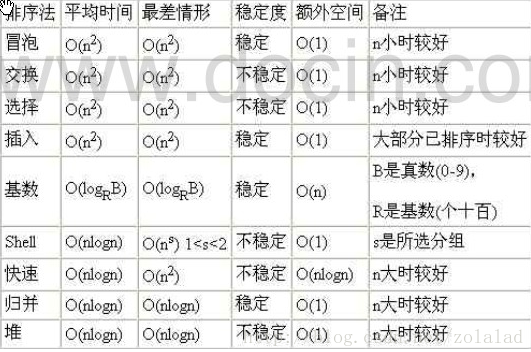
5、空间复杂度

空间复杂度也就是这个算法需要耗费的空间，例如耗费多少内存等，但是现如今大多都是趋向于用空间换时间，因为硬件在不断升级，那么就会有更多的空间得以利用，那么就造成了现在大多数空间换时间的案例，例如缓存数据库，Hibernate缓存等。

记录所用，如有内容有误请谨慎。