svm支持向量机系列(4) --软间隔支持向量机

1、主要内容

　　硬间隔表示实例中的每个点都必须被正确分开， 这样在保证每个点都被正确分开后会造成一个问题就是过拟合的出现，为了解决过拟合问题，引入软间隔的支持向量机，允许少部分的点出错。上节课中讲了kernel技巧，就是将内积和特征转换这两步合成一个步骤来做，移除计算过程中对特征数量d的依赖：

　　

2、软间隔的定义

　　svm的过拟合问题

　　1 转换太过于powerfull

　　2 坚持要将数据完美分开

　　

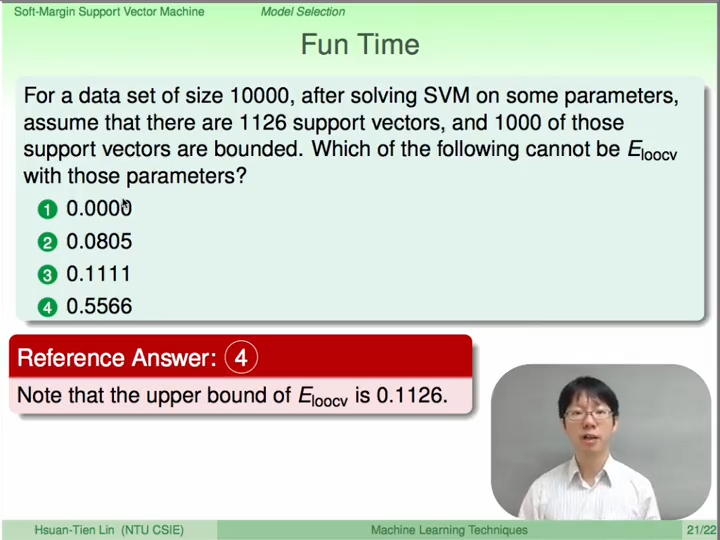
　　为了解决上述的过拟合问题，我们需要放弃某些样本点，允许其出错；

　　

　　结合pocket和hard-margin svm结合起来得出下面的问题：

　　C越大对错误容忍越小，反之C越小对错误的容忍就越大。

　　

　　对于上式可以整理成以下的形式：

　　

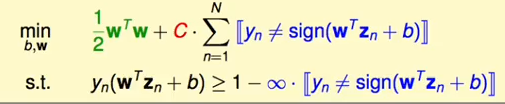
　　对于上述式子，优化问题和条件中都存在符号函数，上式不是一个QP问题不能使用二次规划程序去解，同时不能区分错误的程度；

　　

　　为了解决不能使用二次规划没有对偶形式不能使用kernel的缺陷也不能记录错误大小的缺陷使用下面的式子进行替换：

　　

　　上面的式子中，使用边界违反最为错误的衡量，边界违反变量ξ_n >= 0，对于所有的数据点都成立，如果 ξ_n = 0，那么表示这个点没有错误， 1 > ξ_n > 0则表示该点依然在正确分类但是处在margin内部，ξ_n > 1,则表示该点是错误的，同样依据 ξ_n 的范围可以判断该点处在margin内还是margin外。

　　使用上式之后，非QP问题转化成了QP问题：

　　条件中：增加上了N个ξ_n 的一次限制；

　　目标中：二次问题加上一个一次问题还是一个二次问题；

　　综上：penalize：惩罚，对什么不利； violation ：违反

　　

3、软间隔的对偶问题

　　原始问题：

　　

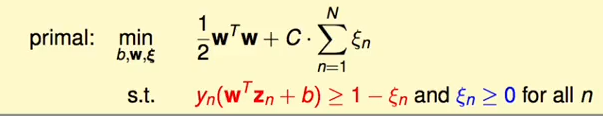
　　对偶问题使用拉格朗日乘子法进行对偶形式的推导：

　　

 　　使用KKT条件进行化简：

　　1、化简α_n和ξ_n

　　对条件求微分为0：

 　　

　　将微分为0 的部分带入：

　　

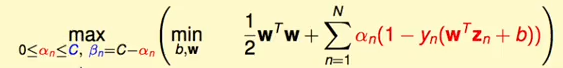
　　2、剩余部分化简

　　对于上式和硬间隔的对偶形式相同：

　　

　　最后可以得到：

　　

　　对于上述问题也是一个凸函数，同样可以使用二次规划问题，与硬间隔唯一不同的就是 α_n有了一个上限，限制条件：

　　

4、核函数软间隔支持向量机

　　

　　与硬间隔不同之处在于限制条件：拉格朗日乘子不再是简单的大于0， 还存在一个上限C；那么此时的KKT条件发生了变化，如何从KKT条件去解b？

　　

　　在硬间隔中：找到一个sv就可以去解b：

　　

　　对于软间隔：

　　

　　因此可以找到一个free sv然后进行b的求解，但是不是都有free sv，一般都会有，没有的话就是一个范围：

　　

5、软间隔支持向量机的实例

　　

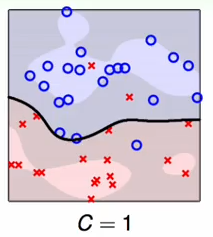
　　此时，对错误不敏感，因此会出现错误；

　　

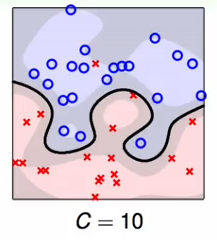
　　此时c = 10表示对错误的容忍度降低，尽量保证每个都被正确分类，此时却无很少；

　　

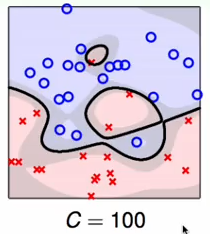
　　c=100 对错误很敏感，保证每一个都正确分类，可能产生过拟合现象。

　　综上c的三个不同的取值表明即使是软间隔的支持向量机也会产生过拟合的现象，因此在实际的使用中一定要注意参数的选择；

　　

　　α_n的物理含义：

　　可以根据α_n的取值的不同进行数据的分析，分析数据在边界内还是边界外以及是否是sv是否是 free sv：

　　

　　形容bounded vector 当 c = α_n 

6、模型的选择

　　

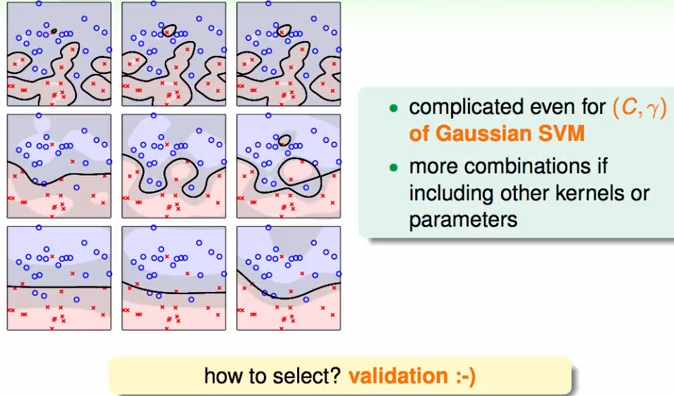
　　选择的另一个方法：使用sv的数据去估计错误的上限；

　　

　　使用支持向量的数量进行模型的选择时，需要注意得到的只是一个上限：

　　

　　

7、fun time