Codeforces 724F 【计数DP】

题意

(;)
给定三个数(n,d,mod)。现在需要你求出，满足有(n)个节点，除了度数为(1)的节点，其它节点的度数都为(d)的不同构的树的数量。输出答案对(mod)取模的结果。

[nleq 1000, ;dleq 10, ;10^8leq mod leq 10^9 ]

Solution

(;)
一般来说，计数类问题需要满足的条件是不能重复，不能遗漏。
什么是不同构？如下三棵树就是同构的

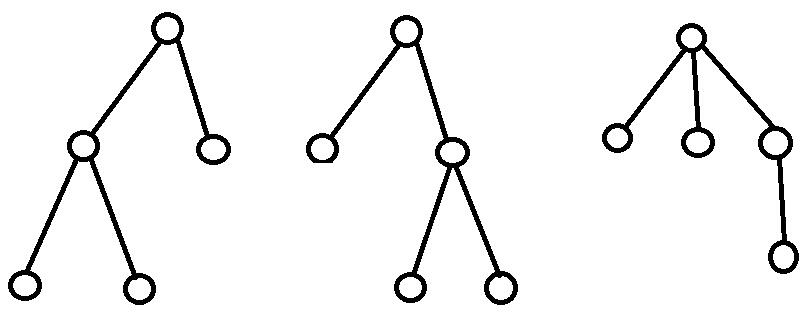
所以我们首先要确定一棵树的根，否则这棵树可能会被重复算多次。
(;)

确定根节点

(;)
但是根节点并不能随便的挑选一个。这里我们挑选重心作为根节点。
原因就在于：重心在一棵树上是唯一的（当然有特殊情况是两个，这个我们后面会陈述），所以对于一棵树来说，它只会在以其重心为根时会被算一次，从而避免了算重复。
而重心还满足什么性质？我们知道，重心将整棵树分成的联通块中最大的那个不超过整棵树大小的一半。
而根据重心的这几条性质，我们就可以考虑进行DP。
(;)

考虑DP

(;)
状态设计：
首先，因为我们最终要得到一颗(n)个节点的树，所以第一维状态表示这棵树有(i)个节点。
其次，由于最终每个点的度数都为(d)，所以第二维状态表示根节点有(j)棵子树。
最后，由于我们要满足根节点是重心的条件，所以第三维状态表示根节点下面的子树大小都不超过(k)
综上所述。(f_{i,j,k})表示(i)个节点，其中根节点有(j)棵子树，且子树大小都不超过(k)的树的数量。
状态转移：
由于树是不同构的，所以我们并不关心子树之间的相对顺序，所以我们DP的时候默认子树是从小到大排的。
因为子树大小都是不超过(k)的，而若子树大小都小于(k)，那么状态转移可得：(f_{i,j,k}=f_{i,j,k-1})
否则说明有若干棵子树大小是等于(k)的，则我们枚举有(t)棵这样的子树，那么除去这(t)棵子树，剩下部分的状态即为(f_{i-t imes k,j-t,k-1})。
而由于子树之间是可以相同的。
所以这(t)棵子树的方案数，实际就是从(f_{k,d-1,k-1})这么多数量中选出(t)棵且可以重复的方案数，即为：(C(f_{k,d-1,k-1}+t-1,t))
那么状态转移可得：(f_{i,j,k}=f_{i-t imes k,j-t,k-1} imes C(f_{k,d-1,k-1}+t-1,t))
(;)

统计答案

(;)
直接输出(f_{n,d,lfloor frac{n}{2} floor})？那说明你太天真了~
注意：这里的DP是基于一棵树只有一个重心的情况。而对于那些有双重心的树，是会被会算两遍的，所以我们要将这种情况减去一遍。
那么我们来分析，什么时候会出现双重心的情况？
显然，只有可能是一条边连接的两个点分别挂着两颗点数相同的子树，如下图：

而我们发现，这种情况一定有偶数个节点。
而对于这种情况的数量，如何求呢？
因为是两个节点分别挂着两颗点数相同的子树，而这样树的数量显然就是(f_{n/2,d-1,n/2-1})
而此时方案数即为从(f_{n/2,d-1,n/2-1})这么多数量选出不重复的两个，即为(C(f_{n/2,d-1,n/2-1},2))
为什么这里必须是不重复？
因为按照我们DP的过程，两边子树相同这样的情况只会被我们算一遍。（因为儿子是可以交换的）
这个地方还需读者稍微理解一下。
综上所述：
当(n)为奇数时，(Ans = f_{n,d,lfloor frac{n}{2} floor})
当(n)为偶数时，(Ans = f_{n,d,lfloor frac{n}{2} floor}-C(f_{n/2,d-1,n/2-1},2))
那么整道题就做完了。
但有一些DP的边界条件还是要多多注意，细节都在代码里。
而且不要忘记要特判，当(nleq 2)时直接输出(1)即可
(;)

Code

#include <bits/stdc++.h>
const int N = 1010;
int n, d, mod, f[N][20][N], fac[20], Inv[20];
int ksm(int a, int b)
{
	int ans = 1;
	while(b)
	{
		if(b & 1) ans = 1LL * ans * a % mod;
		a = 1LL * a * a % mod;
		b >>= 1;
	}
	return ans;
}
int C(int n, int m)
{
	if(m > n) return 0;
	int ans = 1;
	for(int i=n-m+1;i<=n;i++) ans = 1LL * ans * i % mod;
	ans = 1LL * ans * Inv[m] % mod;
	return ans;
}
int main()
{
	scanf("%d%d%d", &n, &d, &mod);
	if(n == 1 || n == 2)
	{
		puts("1");
		return 0;
	}
	fac[0] = Inv[0] = 1;
	for(int i=1;i<=d;i++) fac[i] = 1LL * fac[i - 1] * i % mod;
	Inv[d] = ksm(fac[d], mod - 2);
	for(int i=d-1;i>=1;i--) Inv[i] = 1LL * Inv[i + 1] * (i + 1) % mod;
	for(int i=0;i<=n;i++) f[1][0][i] = 1;
	for(int i=2;i<=n;i++)
	{
		for(int j=1;j<=std::min(d,i-1);j++)
		{
			for(int k=1;k<=n;k++)
			{
				f[i][j][k] = f[i][j][k - 1];
				for(int t=1;t<=j;t++)
				{
					if(i >= t * k && j >= t && k - 1 >= 0)
					{
						//printf("%d
", C(f[k][d - 1][k - 1] + t - 1, t));
						if(k > 1)
						f[i][j][k] = (f[i][j][k] + 1LL * f[i - t * k][j - t][k - 1] * 
						C(f[k][d - 1][k - 1] + t - 1, t) % mod) % mod;
						else
						{
							f[i][j][k] = (f[i][j][k] + 1LL * f[i - t * k][j - t][k - 1] * 
							C(f[k][0][k - 1] + t - 1, t) % mod) % mod;
						}
					}
				}
			}
		}
	}
	int res;
	if(n & 1) 	
		res = f[n][d][n / 2];
	else
		res = (f[n][d][n / 2] - C(f[n / 2][d - 1][n / 2 - 1], 2) + mod) % mod;
	printf("%d", res);
	return 0; 
}