简述分类与聚类的联系与区别。
分类是指在对数据集分类时,我们知道这个数据集是有多少种类的。
聚类是将数据对象的集合分成相似的对象类的过程,使得同一个簇(或类)中的对象之间具有较高的相似性,而不同簇中的对象具有较高的相异性。即指在对数据集操作时,我们是不知道该数据集包含多少类,我们要做的,是将数据集中相似的数据归纳在一起。
简述什么是监督学习与无监督学习。
监督学习是指每个实例都是由一组特征和一个类别结果,拥有标注的数据训练模型,并产生一个推断的功能。对于新的实例,可以用于映射出该实例的类别。
无监督学习是指我们只知道一些特征,并不知道答案,但不同实例具有一定的相似性,然后把那些相似的聚集在一起。
2.朴素贝叶斯分类算法 实例
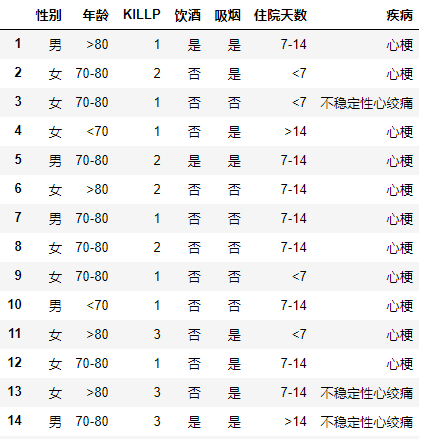
利用关于心脏情患者的临床数据集,建立朴素贝叶斯分类模型。
有六个分类变量(分类因子):性别,年龄、KILLP评分、饮酒、吸烟、住院天数
目标分类变量疾病:–心梗–不稳定性心绞痛
新的实例:–(性别=‘男’,年龄<70, KILLP=‘I',饮酒=‘是’,吸烟≈‘是”,住院天数<7)
最可能是哪个疾病?

3、编程实现朴素贝叶斯分类算法
import pandas as pd
import numpy as np
dataDF = pd.read_excel(r'data/心脏病患者临床数据.xlsx')
# 数据处理,对男女(男1女0),年龄(<70 -1,70-80 0,>80 1),
# 住院天数(<7 -1,7-14 0,>14 1)三个列进行处理
sex = []
for s in dataDF['性别']:
if s == '男':
sex.append(1)
else:
sex.append(0)
age = []
for a in dataDF['年龄']:
if a == '<70':
age.append(-1)
elif a == '70-80':
age.append(0)
else:
age.append(1)
days = []
for d in dataDF['住院天数']:
if d == '<7':
days.append(-1)
elif d == '7-14':
days.append(0)
else:
days.append(1)
# 另外生成一份处理后的DF
dataDF2 = dataDF
dataDF2['性别'] = sex
dataDF2['年龄'] = age
dataDF2['住院天数'] = days
# 转为数组用于计算
dataarr = np.array(dataDF)
dataarr
# 用贝叶斯模型判断病人属于哪种病:性别=‘男’,年龄<70, KILLP=1,饮酒=‘是’,吸烟=‘是”,住院天数<7
def beiyesi(sex, age, KILLP, drink, smoke, days):
# 初始化变量
x1_y1,x2_y1,x3_y1,x4_y1,x5_y1,x6_y1 = 0,0,0,0,0,0
x1_y2,x2_y2,x3_y2,x4_y2,x5_y2,x6_y2 = 0,0,0,0,0,0
y1 = 0
y2 = 0
for line in dataarr:
if line[6] == '心梗':# 计算在心梗条件下出现各症状的次数
y1 += 1
if line[0] == sex:
x1_y1 += 1
if line[1] == age:
x2_y1 += 1
if line[2] == KILLP:
x3_y1 += 1
if line[3] == drink:
x4_y1 += 1
if line[4] == smoke:
x5_y1 += 1
if line[5] == days:
x6_y1 += 1
else: # 计算不稳定性心绞痛条件下出现各症状的次数
y2 += 1
if line[0] == sex:
x1_y2 += 1
if line[1] == age:
x2_y2 += 1
if line[2] == KILLP:
x3_y2 += 1
if line[3] == drink:
x4_y2 += 1
if line[4] == smoke:
x5_y2 += 1
if line[5] == days:
x6_y2 += 1
# print('y1:',y1,' y2:',y2)
# 计算,转为x|y1, x|y2
# print('x1_y1:',x1_y1, ' x2_y1:',x2_y1, ' x3_y1:',x3_y1, ' x4_y1:',x4_y1, ' x5_y1:',x5_y1, ' x6_y1:',x6_y1)
# print('x1_y2:',x1_y2, ' x2_y2:',x2_y2, ' x3_y2:',x3_y2, ' x4_y2:',x4_y2, ' x5_y2:',x5_y2, ' x6_y2:',x6_y2)
x1_y1, x2_y1, x3_y1, x4_y1, x5_y1, x6_y1 = x1_y1/y1, x2_y1/y1, x3_y1/y1, x4_y1/y1, x5_y1/y1, x6_y1/y1
x1_y2, x2_y2, x3_y2, x4_y2, x5_y2, x6_y2 = x1_y2/y2, x2_y2/y2, x3_y2/y2, x4_y2/y2, x5_y2/y2, x6_y2/y2
x_y1 = x1_y1 * x2_y1 * x3_y1 * x4_y1 * x5_y1 * x6_y1
x_y2 = x1_y2 * x2_y2 * x3_y2 * x4_y2 * x5_y2 * x6_y2
# 计算各症状出现的概率
x1,x2,x3,x4,x5,x6 = 0,0,0,0,0,0
for line in dataarr:
if line[0] == sex:
x1 += 1
if line[1] == age:
x2 += 1
if line[2] == KILLP:
x3 += 1
if line[3] == drink:
x4 += 1
if line[4] == smoke:
x5 += 1
if line[5] == days:
x6 += 1
# print('x1:',x1, ' x2:',x2, ' x3:',x3, ' x4:',x4, ' x5:',x5, ' x6:',x6)
# 计算
length = len(dataarr)
x = x1/length * x2/length * x3/length * x4/length * x5/length * x6/length
# print('x:',x)
# 分别计算 给定症状下心梗 和 不稳定性心绞痛 的概率
y1_x = (x_y1)*(y1/length)/x
# print(y1_x)
y2_x = (x_y2)*(y2/length)/x
# 判断是哪中疾病的可能性大
if y1_x > y2_x:
print('该病人患心梗的可能性较大,可能性为:',y1_x)
else:
print('该病人患不稳定性心绞痛的可能性较大,可能性为:',y2_x)
# 判断:性别=‘男’,年龄<70, KILLP=1,饮酒=‘是’,吸烟=‘是”,住院天数<7
beiyesi(1,-1,1,'是','是',-1)
结果为:
1.使用朴素贝叶斯模型对iris数据集进行花分类
尝试使用3种不同类型的朴素贝叶斯:
高斯分布型
from sklearn import datasets iris = datasets.load_iris() from sklearn.naive_bayes import GaussianNB Gaus = GaussianNB() pred = Gaus.fit(iris.data , iris.target) G_pred = pred.predict(iris.data) print(iris.data.shape[0],(iris.target !=G_pred).sum()) print(iris.target)

伯努利型
from sklearn.naive_bayes import BernoulliNB from sklearn import datasets iris = datasets.load_iris() Bern = BernoulliNB() pred = Bern.fit(iris.data, iris.target) B_pred = pred.predict(iris.data) print(iris.data.shape[0],(iris.target !=B_pred).sum()) print(iris.target) print(B_pred)

多项式型
from sklearn import datasets from sklearn.naive_bayes import MultinomialNB iris = datasets.load_iris() Mult = MultinomialNB() pred = Mult.fit(iris.data, iris.target) M_pred = pred.predict(iris.data) print(iris.data.shape[0],(iris.target !=M_pred).sum()) print(iris.target) print(M_pred) print(iris.target !=M_pred)

2.使用sklearn.model_selection.cross_val_score(),对模型进行验证。
from sklearn.naive_bayes import GaussianNB
from sklearn.model_selection import cross_val_score
gnb = GaussianNB()
scores = cross_val_score(gnb,iris.data,iris.target,cv=10)
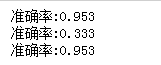
print("准确率:%.3f"%scores.mean())
from sklearn.naive_bayes import BernoulliNB
from sklearn.model_selection import cross_val_score
Bern = BernoulliNB()
scores = cross_val_score(Bern,iris.data,iris.target,cv=10)
print("准确率:%.3f"%scores.mean())
from sklearn.naive_bayes import MultinomialNB
from sklearn.model_selection import cross_val_score
Mult = MultinomialNB()
scores = cross_val_score(Mult,iris.data,iris.target,cv=10)
print("准确率:%.3f"%scores.mean())
3. 垃圾邮件分类
数据准备:
- 用csv读取邮件数据,分解出邮件类别及邮件内容。
- 对邮件内容进行预处理:去掉长度小于3的词,去掉没有语义的词等
(1)读取数据集
import csv
file_path = r'D:shujuSMSSpamCollectionjsn.txt'
mail = open(file_path,'r',encoding='utf-8')
mail_data=[]
mail_label=[]
csv_reader = csv.reader(mail,delimiter=' ')
for line in csv_reader:
mail_data.append(line[1])
mail_label.append(line[0])
mail.close()
mail_data

(2)邮件预处理
import nltk
from nltk.corpus import stopwords
from nltk.stem import WordNetLemmatizer
from sklearn.naive_bayes import MultinomialNB as MNB
def preprocessing(text):
#text=text.decode("utf-8)
tokens=[word for sent in nltk.sent_tokenize(text) for word in nltk.word_tokenize(sent)] #nltk进行分词
stops=stopwords.words('english') #去掉停用词
tokens=[token for token in tokens if token not in stops]
tokens=[token.lower() for token in tokens if len(token)>=3] #去掉大小写
lmtzr=WordNetLemmatizer() #词性还原
tokens=[lmtzr.lemmatize(token) for token in tokens]
preprocessed_text=' '.join(tokens)
return preprocessed_text
(3)导入数据
import csv
file_path=r'H:作业py数据挖掘基础算法2018.12.3SMSSpamCollectionjsn.txt'
sms=open(file_path,'r',encoding='utf-8')
sms_data=[]
sms_label=[]
csv_reader=csv.reader(sms,delimiter=' ')
for line in csv_reader:
sms_label.append(line[0])
sms_data.append(preprocessing(line[1]))
sms.close()
(4)训练集与测试集:将先验数据按一定比例进行拆分。
import numpy as np sms_data=np.array(sms_data) sms_label=np.array(sms_label) from sklearn.model_selection import train_test_split x_train, x_test, y_train, y_test =train_test_split(sms_data, sms_label, test_size=0.3, random_state=0, stratify=sms_label) #按训练集和测试集0.7:0.3划分 print(len(sms_data),len(x_train),len(x_test)) x_train

(5)提取数据特征,将文本解析为词向量 。
from sklearn.feature_extraction.text import TfidfVectorizer vectorizer=TfidfVectorizer(min_df=2,ngram_range=(1,2),stop_words='english',strip_accents='unicode',norm='l2') X_train=vectorizer.fit_transform(x_train) X_test=vectorizer.transform(x_test)
(6)训练模型:建立模型,用训练数据训练模型。即根据训练样本集,计算词项出现的概率P(xi|y),后得到各类下词汇出现概率的向量 。
X_train
a=X_train.toarray()
print(a)
for i in range(1000):
for j in range(5984):
if a[i,j]!=0:
print(i,j,a[i,j])

(7)
测试模型:用测试数据集评估模型预测的正确率。
混淆矩阵
准确率、精确率、召回率、F值
from sklearn.naive_bayes import MultinomialNB as MNB
from sklearn.metrics import confusion_matrix
from sklearn.metrics import classification_report
clf=MNB().fit(X_train,y_train)
y_nb_pred=clf.predict(X_test)
print(y_nb_pred.shape, y_nb_pred)
print('nb_confusion_matrix:') #混淆矩阵
cm = confusion_matrix(y_test, y_nb_pred)
print(cm) #准确率、精确率、召回率、F值
cr = classification_report(y_test, y_nb_pred)
print(cr)
feature_names = vectorizer.get_feature_names()
coefs = clf.coef_
intercept = clf.intercept_
coefs_with_fns = sorted(zip(coefs[0], feature_names))
n = 10
top = zip(coefs_with_fns[:n], coefs_with_fns[:-(n + 1):-1]) #
for (coef_1, fn_1), (coef_2, fn_2) in top:
print(' %.4f %-15s %.4f %-15s' % (coef_1, fn_1, coef_2, fn_2))
