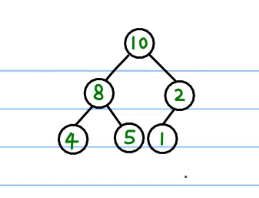
堆
条件
完全二叉树 + 父节点要大于 子节点
步骤1
需要在导数第二行进行构建堆 , 把大的取到父节点的位置上
步骤2
排序输出堆,将最大的节点跟最后一个节点进行交换数值 然后把最大的节点放在最后的位置上,然后对新的节点进行构建堆
java
public class Heap {
private static int arr[];
public static void swap(int tree[], int max, int i) {
int temp = tree[max];
tree[max] = tree[i];
tree[i] = temp;
}
public static void heapify(int tree[], int n, int i) { // 对指定的点进行heapify
if (i >= n)
return;
int c1 = i * 2 + 1;
int c2 = i * 2 + 2;
int max = i; //用max 代替flag :1?2 这个
if (c1 < n && tree[max] < tree[c1])
max = c1;
if (c2 < n && tree[max] < tree[c2])
max = c2;
if (i != max) {
swap(tree, max, i);
heapify(tree, n, max); //因为进行了交换所以需要对该节点下面进行调整
//有可能上面换下来的数 比根节点还小 所以需要进行 彻底的交换
}
}
// 乱序 则需要对所有点进行 heapify
public static void build_heaptree(int arr[], int n) {
int i = (n - 2) / 2; // last_node_parent
for (; i >= 0; i--) {
heapify(arr, n, i);
}
for (int x = 0; x < n; x++) {
System.out.println(arr[x]);
}
}
public static void main(String[] args) {
arr = new int[] { 2, 1, 5, 3, 10, 4 };
int n = 6;
build_heaptree(arr, n);
}
}