2202.最大三角形 --计算几何

参考https://www.cnblogs.com/xiexinxinlove/p/3708147.html
https://blog.csdn.net/MyHeaven7/article/details/52193566?utm_source=blogxgwz7
排序问题https://www.cnblogs.com/xudong-bupt/p/3168618.html
https://blog.csdn.net/qq_39630587/article/details/79264119
                    B站搜索 convex hull
原本的思路就是通过原点找一个最远点 还有一个最近点 连线构成一个直径，然后找每个点
到圆心的距离进行计算，然后我发现与原点构成等腰三角形就不能判断。
我就这样为实现了 但是如果有多条边都为最长 则方法不好 pass；
https://blog.csdn.net/jiang199235jiangjj/article/details/7954512
https://www.bilibili.com/video/av9005901/?p=12、
https://blog.csdn.net/qq_41268947/article/details/81389133
https://www.bilibili.com/video/av27279886/?spm_id_from=333.788.videocard.0(视频后面有)
分为上凸包下凸包进行 进行筛选 筛选完也就省几个在凸包上

import java.util.Arrays;
import java.util.Comparator;
import java.util.Scanner;
class Point {
	int x;
	int y;
}
//比较函数
class myComparator implements Comparator<Point> {
	public int compare(Point p1, Point p2) {
		if (p1.x != p2.x)
			return p1.x > p2.x ? 1 : -1;
		else {
			return p1.y > p2.y ? 1 : -1;
		}
	}
}
public class Main {
	static Point[] a = new Point[50005];// sort 要指定范围 不然会把没放进去的对象也进行排序 导致报错NullException
	static Point[] b = new Point[50005];// 存放凸包上的坐标
	public static double length(double x, double y, double x1, double y1) {
		return Math.sqrt((x1 - x) * (x1 - x) + (y1 - y) * (y1 - y));
	}
	// 通过坐标计算面积大小 向量求解 //用三个点进行计算
	public static int Count(Point i, Point j, Point k) {
		int x1 = i.x - j.x;
		int y1 = i.y - j.y;
		int x2 = k.x - j.x;
		int y2 = k.y - j.y;
		return (x1 * y2 - x2 * y1);
	}
	public static int convex(int n) {
		Arrays.sort(a, 0, n, new myComparator());// 在继承那里定义一下泛型 就不会有警告
		int m = 0;
		for (int i = 0; i < n; i++) {
			while (m > 1 && Count(b[m - 1], a[i], b[m - 2]) <= 0)
				m--;
			b[m++] = a[i];
		}
		int k = m;//可不能把上凸包找到点push出来
		for (int i = n - 2; i >= 0; i--) {
			while (m > k && Count(b[m - 1], a[i], b[m - 2]) <= 0)//向量面积计算
				m--;
			b[m++] = a[i];
		}
		if (n > 1)
			m--;
		return m;
	}
	public static void main(String[] args) {
		Scanner sc = new Scanner(System.in);
		while (sc.hasNext()) {
			int n = sc.nextInt();
			for (int i = 0; i < n; i++) {
				Point temp = new Point();
				temp.x = sc.nextInt();
				temp.y = sc.nextInt();
				a[i] = temp;
			}
			double sum = 0;
			// for(int i = 0 ; i < n ; i++) {
			// System.out.println(a[i].x+" "+a[i].y);
			// }//通过这个地方进行验证排序完的结果
			int m = convex(n);
			for (int i = 0; i < m; i++)// m个凸包
				for (int j = i + 1; j < m; j++)
					for (int k = j + 1; k < m; k++) {
						sum = Math.max(sum, Count(b[i], b[j], b[k]));
					}
			System.out.println(String.format("%.2f", sum / 2));
		}
	}
}

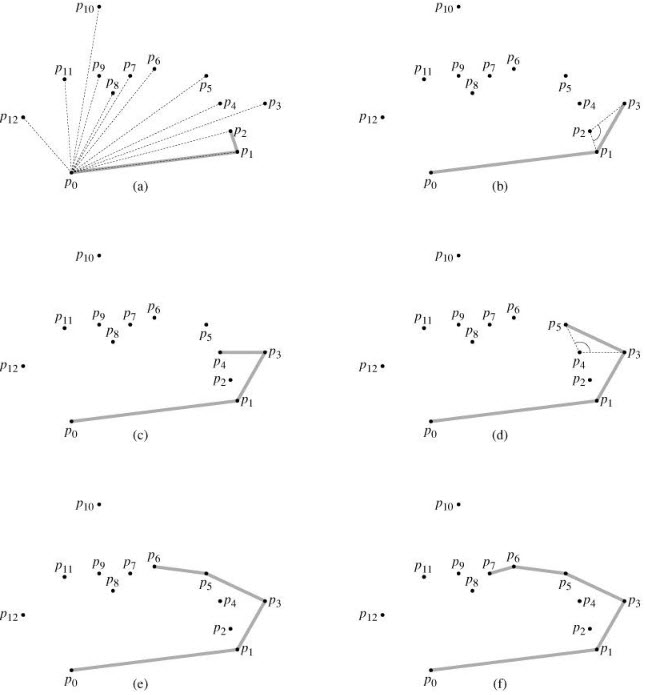
另外一种是从最小点一步一步逆时针搜索 结合向量三角形面积判断正负