轮廓线DP
刚刚学了轮廓线DP,想了好久才懂。
我的理解就是用一条线的状态去更新另一条线的状态,然后将格子填满。
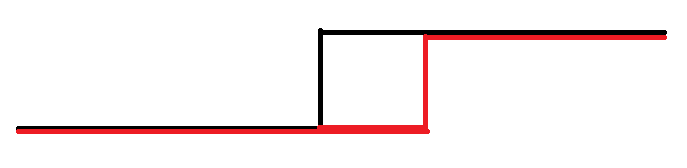
图中正方形即是要填东西(根据题意)的格子,红线的状态是由黑线转移过来的。
对于每一条线都有一个自己的状态(一个二进制数,先不用看1和0是啥意思),如下图。
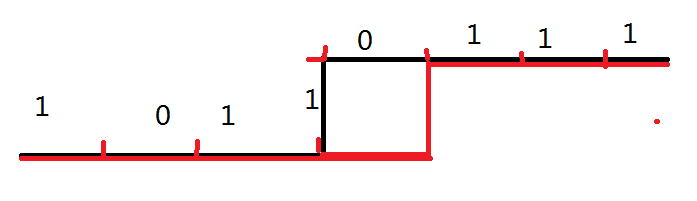
图中黑线的状态即是11101101(最左边的是二进制位第零位),编号从左往右为1,2,3,4,5,6,7,8。
具体一点,我们上例题。
题目大意:给你一个\(n*m\)\((1 <= n,m <= 100)\)的网格,让你在网格里填上长度不小于2的线段,问有多少种情况,对结果%\(1e9 + 7\)。
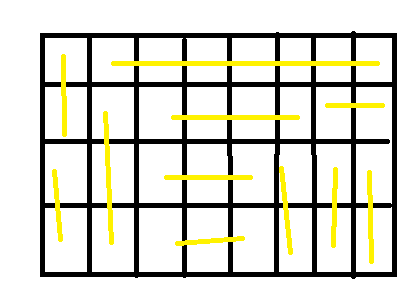
这是某一种情况。
现在我们轮廓线上的1和0就有意义了:如果竖着的这条线上的数为1的话,那么这个格子必须画一条横线(图一);如果横着的这条线上的数为1的话,那么这个格子必须画一条竖线(图二);我们发现,横线和竖线上不能同时为1,这是冲突的;如果横线和竖线上都为0,那么这个格子里话横线竖线都可以。
(不会画图,丑死了)
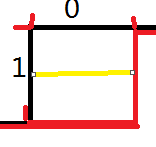 (图一)
(图一)
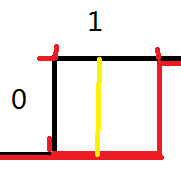 (图二)
(图二)
下面为了好打,把图一定义为(1, 0),图二定义为(0,1)。\(a[]\)是二进制数,\(i\)是下标:(\(a[i - 1]\), \(a[i]\))
对于一个格子,它上面的黑线有三种情况:(1, 0),(0, 1),(0, 0)。然后我们考虑怎么将黑线的状态转移到红线。
<1> 当黑线为(1,0)时,红线可以转移到的状态有:(0,1),(0,0)。(其他位上二进制数都一样)
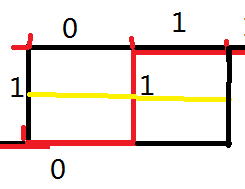

<2> 当黑线为(0,1)时,红线可以转移到的状态有:(1,0),(0,0)。
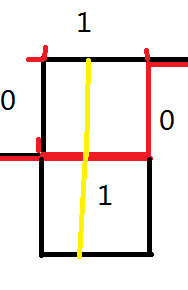
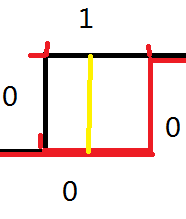
<3> 当黑线为(0,0)时,红线可以转移到的状态有:(0,1),(1,0)。(差不多,就不画了)
像这样一直转移下去,填完\(n*m\)个格子,就可以得到所有的方案。
我们考虑开一个二维\(unordered\) _ \(map\),\(unordered\)_\(map<int , long long> dp[2]\);\(dp[0,1][x] = val\),第一维是个滚动数组,第二维\(x\)是这条轮廓线的状态,\(val\)是这条线填完对应的那个格子后合法的方案数。
为啥用\(unordered\)\(map\),而不用\(map\)呢?\(map\): 该类型的搜索时间复杂度为\(O(logn)\) ;\(unordered_map\) : 搜索时间复杂度\(O(1)\)为平均时间,最坏情况下的时间复杂度为\(O(n)\);
#include <iostream>
#include <cstdio>
#include <unordered_map>
using namespace std;
const int p = 1e9 + 7;
int n, m;
void work(int n, int m) {
unordered_map <int, long long> dp[2];
int now = 0, nxt = 1;
dp[now][0] = 1;
for(int i = 1;i <= n; i++) {
for(int j = 1;j <= m; j++) {
dp[nxt].clear();
for(auto k = dp[now].begin();k != dp[now].end(); k++) {
int nowst = k -> first, nowval = k -> second;
int u = (nowst >> j) & 1, l = (nowst >> (j - 1)) & 1;
if(u == 0 && l == 0) {
(dp[nxt][nowst ^ (1 << j)] += nowval) %= p;
(dp[nxt][nowst ^ (1 << (j - 1))] += nowval) %= p;
}
else if(u == 1 && l == 0) {
(dp[nxt][nowst ^ (1 << j)] += nowval) %= p;
(dp[nxt][nowst ^ (1 << j) ^ (1 << (j - 1))] += nowval) %= p;
}
else if(u == 0 && l == 1) {
(dp[nxt][nowst ^ (1 << (j - 1))] += nowval) %= p;
(dp[nxt][nowst ^ (1 << j) ^ (1 << (j - 1))] += nowval) %= p;
}
}
swap(now, nxt);
}
dp[nxt].clear();
for(auto k = dp[now].begin();k != dp[now].end(); k++) {
int nowst = k -> first, nowval = k -> second;
if((nowst >> m) ^ 1) dp[nxt][nowst << 1] = nowval;
}
swap(now, nxt);
}
printf("%d", dp[now][0]);
}
int main() {
scanf("%d %d", &n, &m);
work(n, m);
return 0;
}
我也是刚学,哪说的不对的还希望大佬指出。