在我们遇到回归问题时,例如前面提到的线性回归,我们总是选择最小而成作为代价函数,形式如下:

这个时候,我们可能就会有疑问了,我们为什么要这样来选择代价函数呢?一种解释是使我们的预测值和我们训练样本的真实值之间的距离最小,下面我们从概率的角度来进行解释。
首先假设输入变量和目标变量满足下面的等式
![]()
ε(i)指的是误差,表示我们在建模过程中没有考虑到的,但是它对预测的结果又有影响。它是独立同分布(IID:independently and identically distributed)的高斯分布。 (可以看看中心极限定理)
(可以看看中心极限定理)
所以我们可以得到
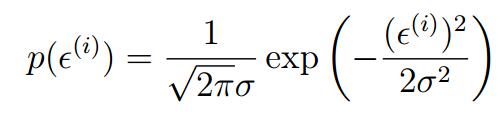
将现行回归方程代入我们可以得到

其中符号  表示以θ 为参数,给定
表示以θ 为参数,给定  时
时  的分布。如果给定
的分布。如果给定  (设计矩阵,包括所有的
(设计矩阵,包括所有的  )和 ,则目标变量的分布可以写成
)和 ,则目标变量的分布可以写成 ,所以我们可以将它看成是关于
,所以我们可以将它看成是关于 的函数。同样,从另外一个角度,我们可以把它看成是关于θ的函数,这个函数称之为似然函数(likelihood function),形式如下:
的函数。同样,从另外一个角度,我们可以把它看成是关于θ的函数,这个函数称之为似然函数(likelihood function),形式如下:

由于已经假设  独立同分布,所以我们可以写成如下形式
独立同分布,所以我们可以写成如下形式
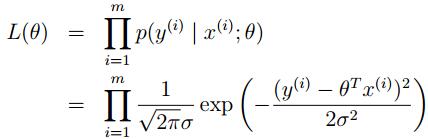
这样我们就得到了y(i) 和x(i)之间的关系模型,这样问题就来了,我们该怎么去学习参数θ 呢?
在运用似然函数求解时候,我们一般运用最大似然估计,它的思想是:已知某个参数能使这个样本出现的概率最大,我们当然不会再去选择其他小概率的样本,所以干脆就把这个参数作为估计的真实值。也即,我们取L(θ)最大时候的θ值。
求解过程:
先对似然函数取对数,然后求解
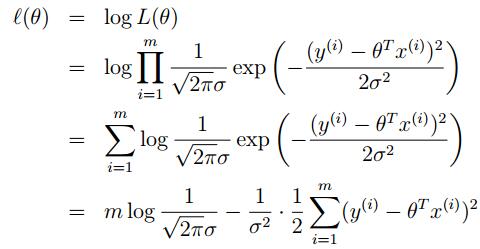
所以对于 取最大,则要求
取最大,则要求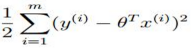 取最小,也即我们的代价函数。
取最小,也即我们的代价函数。
至此,我们最大化似然函数l(Θ),等价于最小化损失函数J(Θ),这也说明了在我们的推导中,最后结果与我们假设的高斯分布的方差σ是没有关系的。
回过头来再考虑一下,我们假设了什么,我们假设误差项服从高斯分布,这个假设对于线性回归模型来说非常形象,其实我们一开始就假设了这个模型是一个线性模型,那么很自然的我们会考虑误差一定是离线性函数越近可能性越大,离线性函数越远可能性越小。所以在机器学习模型中,假设对于我们来说相当重要。