基本性质
优先级队列,也叫二叉堆、堆(不要和内存中的堆区搞混了,不是一个东西,一个是内存区域,一个是数据结构)。
堆的本质上是一种完全二叉树,分为:
-
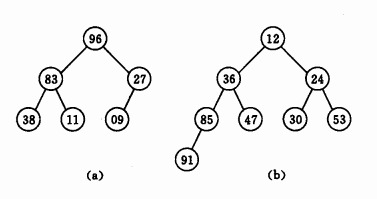
最小堆(小根堆):树中每个非叶子结点都不大于其左右孩子结点的值,也就是根节点最小的堆,图(a)。
-
最大堆(大根堆):树中每个非叶子结点都不小于其左右孩子结点的值,也就是根节点最大的堆,图(b)。
基本操作
均以大根堆为例
存储方式
堆本质上是一颗完全二叉树,使用数组进行存储,从(a[1])开始存储,这样对于下标为(k)的结点(a[k])来说,其左孩子的下标为(2*k),右孩子的下标为(2*k+1)。,且不论 (k) 是奇数还是偶数,其父亲结点(如果有的话)就是 $left lfloor k/2 ight floor $。
向上调整
假如我们向一个堆中插入一个元素,要使其仍然保持堆的结构。应该怎么办呢?
可以把想要添加的元素放在数组的最后,也就是完全二叉树的最后一个结点的后面,然后进行向上调整(heapinsert)。向上调整总是把欲调整结点与父亲结点比较,如果权值比父亲结点大,那么就交换其与父亲结点,反复比较,直到到达堆顶或父亲结点的值较大为止。向上调整示意图如下:

代码如下,时间复杂度为(O(logn)):
void heapinsert(int* arr, int n) {
int k = n;
//如果 K 结点有父节点,且比父节点的权值大
while (k > 1 && arr[k] > arr[k / 2]) {
//交换 K 与父节点的值
swap(arr[k / 2], arr[k]);
k >>= 1;
}
}
这样添加元素就很简单了
void insert(int* arr, int n, int x) {
arr[++n] = x;//将x置于数组末尾
heapinsert(arr, n);//向上调整x
}
向下调整
假如我们要删除一个堆中的堆顶元素,要使其仍然保持堆的结构。应该怎么办呢?
移除堆顶元素后,将最后一个元素移动到堆顶,然后对这个元素进行向下调整(heapify),向下调整总是把欲调整结点 (K) 与其左右孩子结点比较,如果孩子中存在权值比当前结点 (K) 大的,那么就将其中权值最大的那个孩子结点与结点 (K),反复比较,直到到结点 (K) 为叶子结点或结点 (K) 的值比孩子结点都大为止。向下调整示意图如下:

代码如下,时间复杂度也是(O(logn)):
void heapify(int* arr, int k, int n) {
//如果结点 K 存在左孩子
while (k * 2 <= n) {
int left = k * 2;
//如果存在右孩子,并且右孩子的权值大于左孩子
if (left + 1 <= n && arr[left] < arr[left + 1])
left++; //就选中右孩子
//如果节点 K 的权值已经大于左右孩子中较大的节点
if (arr[k] > arr[left])
break;
swap(arr[left], arr[k]);
k = left;
}
}
这样删除堆顶元素也就变得很简单了
void deleteTop(int* arr, int n) {
arr[1] = arr[n--];//用最后一个元素覆盖第一个元素,并让n-1
heapify(arr, 1, n);
}
建堆
自顶向下建堆
自顶向下建堆的思想是,从第 (i=1) 个元素开始,对其进行向上调整,始终使前 (i) 个元素保持堆的结构。时间复杂度 (O(nlogn))
void ArrayToHeap(int *a,int n) {
for (int i = 1; i <= n; i++) {
heapinsert(a, i);
}
}
自底向上建堆
自底向上建堆的思想是,从底 $i=left lfloor n/2 ight floor $ 个元素开始,对其进行向下调整,始终让后 (n-i) 个元素保持堆的结构。
void ArrayToBheap(int *a, int n) {
int i = n / 2;
for (; i >= 1; i--) {
heapify(a, i, n);
}
}
如果仅从代码上直观观察,会得出构造二叉堆的时间复杂度为(O(nlogn))的结果。当然这个上界是正确的,但却不是渐近界,可以观察到,不同结点在运行 heapify 的时间与该结点的树高(树高是指该结点到最底层叶子结点的值,不要和深度搞混了)相关,而且大部分结点的高度都很小。利用以下性质可以得到一个更准确的渐近界:
- 一个高度为 (h) 含有 (n) 个元素的堆,有 (h=lfloor logn floor) ,最多包含 (lceil frac{n}{2^{k+1}} ceil) 高度为 (k) 的结点
【可以画颗树试一下,具体证明请看算法导论】
在一个高度为 (h) 的结点上运行 heapify 的代价为 (O(h)),我们可以将自顶向下建堆的总复杂度表示为
这个式子
其实就是求前 (n) 项和,高中数学的知识
到这儿就需要求极限,高等数学的知识 (frac{1}{2^{k-1}}) 当 (k) 趋于无穷大时极限是 (0),对 (frac{k}{2^{k}}) 用洛必达法则极限也是 (0)
也就是说当 (h) 趋向于无穷大时,(O(nsum ^{h} _{k=0}frac {k}{2^{k}})=O(ncdot 2)) ,去掉常数项,所以自底向上建堆复杂度为 (O(n))
堆排序
堆排序的思想:假设一个大根堆有 (n) 个元素,每次把第 (1) 个元素,与第 (n) 个元素交换,对第一个元素进行向下调整(heapify),并使得 (n=n-1) ,直到 (n=1)
void heapSort(int* arr, int n) {
//先自底向上建堆
int i = n / 2;
for (; i >= 1; i--) {
heapify(arr, i, n);
}
for (int i = 50; i > 1; i--) {
swap(arr[1], arr[i]);
heapify(arr, 1, i - 1);
}
}
例题
寻找第K大元素
首先用数组的前k个元素构建一个小根堆,然后遍历剩余数组和堆顶比较,如果当前元素大于堆顶,则把当前元素放在堆顶位置,并调整堆(heapify)。遍历结束后,堆顶就是数组的最大k个元素中的最小值,也就是第k大元素。
void heapify(int* a, int index, int length) {
int left = index * 2 + 1;
while (left <= length) {
if (left + 1 <= length - 1 && a[left + 1] > a[left])left++;
if (a[index] > a[left])break;
swap(a[index], a[left]);
index = left;
}
}
void ArrayToBheap(int* a, int length) {
int i = length / 2 - 1;
for (; i >= 0; i--) {
heapify(a, i, length);
}
}
void FindKMax(int* a, int k, int length) {
ArrayToBheap(a, k);
for (int i = k; i < length; i++) {
if (a[i] > a[0]) a[0] = a[i];
heapify(a, 0, k);
}
}
时间复杂度(O(n)),只是举个例子。
事实上对于这个问题是有更快的做法的,快速排序的思想,时间复杂度 (O(logn))
int Search_K(int left, int right, int k) {
int i = left, j = right;
int p = rand() % (right - left + 1) + left;
int sign = a[p];
swap(a[p], a[i]);
while (i < j) {
while (i < j && a[j] >= sign)j--;
while (i < j && a[i] <= sign)i++;
swap(a[i], a[j]);
}
swap(a[i], a[left]);
if (i - left + 1 == k)return a[i];
if (i - left + 1 < k)return Search_K(i + 1, right, k - (i - left + 1));
else return Search_K(left, i - 1, k);
}
堆更多时候,因为它建堆(O(n)),调整(O(logn)),当需要有序得到某些数据,是要优于排序((O(nlogn)))算法的,而且如果数据规模是动态增加的,那堆就要完全优于排序算法了,在C++的STL是有堆的实现的,叫做 priority_queue 。