引入
AOE网和AOV网
上一篇的拓扑排序中提到了AOV网(Activity On Vertex Network),与之相对应的是AOE网(Activity on edge network),即边表示活动的网。
AOV用顶点表示活动的网,描述活动之间的制约关系。
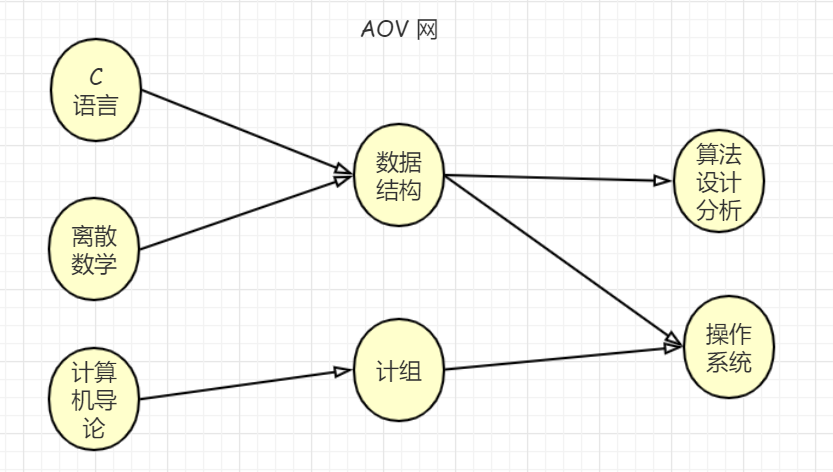
AOE是带权值的有向图,以顶点表示事件,以边表示活动,边上的权值表示活动的开销(如项目工期)。AOE 是建立在子过程之间的制约关系没有矛盾的基础之上,再来分析整个过程需要的开销。所以如果给定AOV网中各顶点活动所需要的时间,则可以转换为AOE网,较为简单的方法就是把每个顶点都拆分成两个顶点,分别表示活动的起点和终点
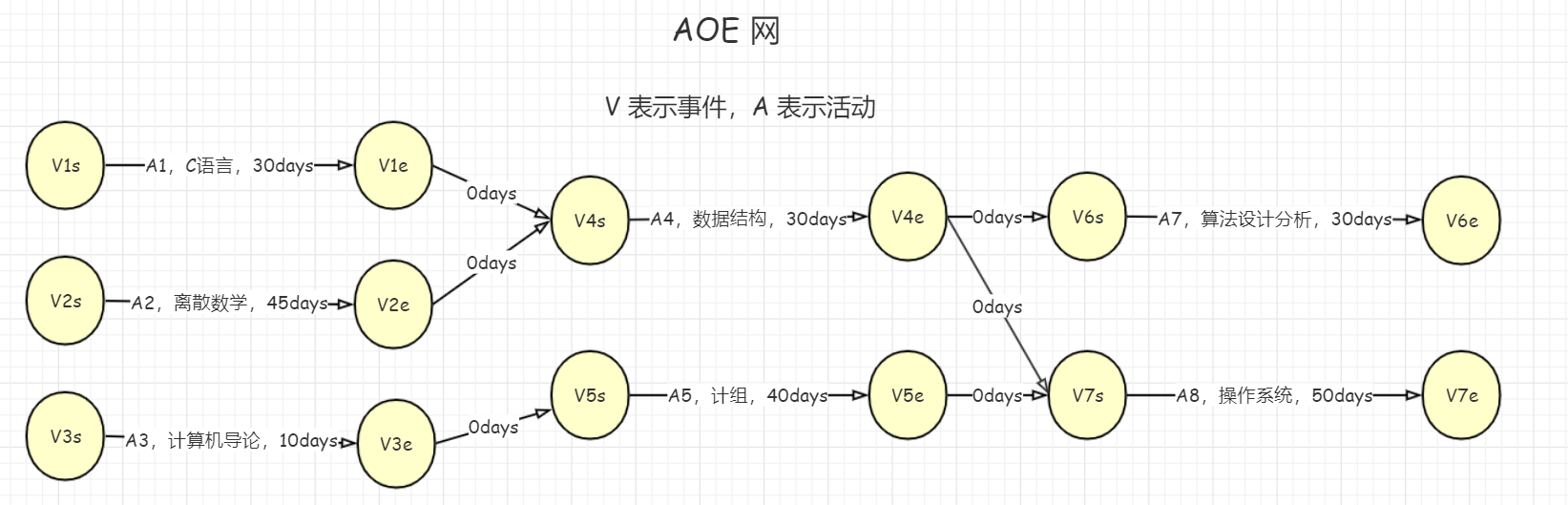
事件和活动
把上图转换成一般的AOE图如下
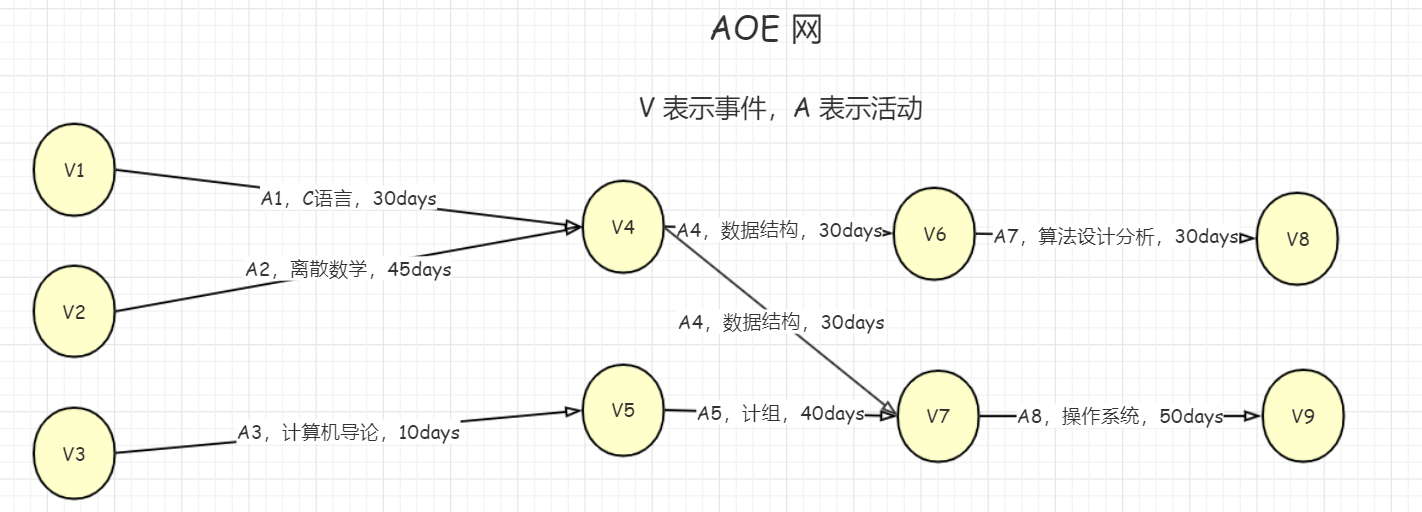
“活动”表示学习课程的过程,而“事件”表示的是一个时间点或者说一种状态(自己的理解),开始和完成活动是一个事件,比如:V4表示学完C语言。而这个事件同时也代表这前面的课程都已经学完了,可以开始学后面的课程了。
关键路径
AOE一般用来估算工程的完成时间。AOE表示工程的流程,把没有入边的称为始点或者源点,没有出边的顶点称为终点或者汇点。一般情况下,AOE只有一个源点一个汇点。但上面用的例图就不止一个,如果碰到这种情况,就可以再加一个“超级源(终)点”,连接所有入(出)度为0的点(不加也不会影响最后的答案)。
关键路径:从源点到汇点具有最长路径(强调:就是AOE网中权值和最大的路径),在关键路径上的活动叫关键活动。但为什么是最大长度呢?
关键路径是AOE网中的最长路径,也是整个工程的最短完成时间,如何理解此处的“最长”和“最短”呢?比如我们想要把“算法设计分析”学完,那么需要的时间就是$max(A1,A2)+(A4)+(A7) = 105days$,那么这105days是最长路径,也是整个工程的最短完成时间,如果我们试图缩短学习的时间,那么缩短“C语言”课程的学习时间显然是没有用的。只有缩短关键路径上的关键活动时间才可以减少整个项目的时间。比如让“离散数学”的时间缩短为30days,则总时间就会减少为90days。
来看四个定义(活动是一个过程,用“开始”,事件是一个时间点,用“发生”):
活动的最早开始时间 ETE(earliest time of edge):所有前导活动都完成,可以开始的时间。
活动的最晚开始时间 LTE(latest time of edge):不推迟工期的最晚开工时间。
事件的最早发生时间 ETV(earliest time of vertex):可以等价理解为旧活动的最早结束时间 或 新活动的最早开始时间
事件的最晚发生时间 LTV(latest time of vertex):可以等价理解为就活动的最晚结束时间 或 新活动的最晚开始时间
举例说明一下,“数据结构”课程的活动最早开始时间就是“离散数学”学完,45days。对于“C语言”课程来说,需要30days,而“离散数学”需要45days,那么“C语言”在“离散数学”开始后的15days,再开始也不会延迟整个学习的时间,这就是活动最晚开始时间。
算法描述
我们把关键路径上的活动称作关键活动,那么对于关键活动来说,它们是不允许拖延的,因此这些活动的最早开始时间必须是等于最晚开始时间,同理,把关键路径上的事件称作关键事件,他们的最早发生时间也是等于最晚发生时间。因此可以设置数组$E$和$L$,其中$E[r]$和$L[r]$分别表示活动$A_r$的最早开始时间和最晚开始时间,于是,我们只要求出这两个数组就可以通过判断$E[r]==L[r]$来确定$r$是否为关键活动了。
再引入两个新的数组$VE$和$VL$,其中$VE[i]$和$VL[i]$分别表示事件$i$的最早发生时间和最晚发生时间。
举个例子,看下图
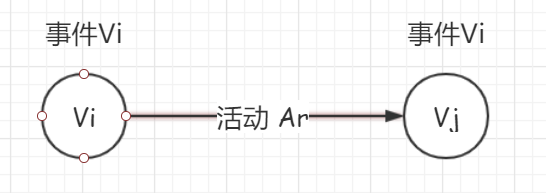
我们可以得出以下四个等式
1.事件$V_i$的最早发生时间就是活动$A_r$的最早开始时间,即$E[r]=VE[i]$
2.事件$V_j$的最早发生时间就是活动$A_r$的最早开始时间$+$活动$A_r$的权值,即$E[r]+length[r]=VE[j]$
3.事件$V_i$的最晚发生时间就是活动$A_r$的最晚开始时间,即$VL[i]=L[r]$
4.事件$V_j$的最晚发生时间就是活动$A_r$的最晚开始时间$+$活动$A_r$的权值,即$VL[j]=L[r]+length[r]$
把1、2合起来就是$VE[j]=VE[i]+length[r]$,把3、4合起来就是$VL[i]=VL[j]-length[r]$,这样我们就可以先要求出$VE$和$VL$这两个数组,然后通过上面的等式得到$E$和$L$数组。
求VE数组
根据$VE[j]=VE[i]+length[r]$,假设我们已知了事件$V_{i1},...V_{ik}$的最早发生时间$VE[i_{1}]....VE[i_{k}]$,那么事件$V_j$的最早发生时间就是$max(VE[i_{1}]+length[r_{1}],...,VE[i_{k}]+length[r_{k}])$,取最大值就是所有能到达$V_j$的活动中最后一个完成的时间,因为只有它们都完成后,$V_j$才算“激活”。
也就是有这样一个式子$$VEleft[ j ight] =max left( VEleft[ i_{p} ight] +lengthleft[ r_{p} ight] ight), p=1,2,...,k$$
如果要计算出$VE[j]$的正确值,就必须在访问$V_j$之前$VE[i_{1}]....VE[i_{k}]$都已经得到,也就是在访问某个结点的时候保证它的前驱结点都已经访问完毕了,这就需要用到上一篇的拓扑排序了,此部分代码如下:
const int N = 30000; vector<pair<int, int>>G[N + 5];//first是下一个结点、second是权值 stack<int>topoOrder; void topologicalSort() { queue<int >q; for (int i = 1; i <= n; i++) if (inDegree[i] == 0) q.push(i); while (!q.empty()) { int u = q.front(); q.pop(); topoOrder.push(u); for (int i = 0; i < G[u].size(); i++) { int v = G[u][i].first; if (--inDegree[v] == 0) { q.push(v); } //用VE[u]来更新u的后继结点 VE[v] = max(VE[u] + G[u][i].second, VE[v]); } } }
求VL数组
同理,根据$VL[i]=VL[j]-length[r]$,假设已经算好了事件$V_{j1},...V_{jk}$的最晚发生时间$VL[j_{1}]....VL[j_{k}]$,那么事件$V_i$的最晚发生时间就是$min(VL[j_{1}]-length[r_{1}],...,VL[j_{k}]-length[r_{k}])$,取最小值就是取所有从$V_i$出发的活动的最早开始的时间,因为必须满足所有$V_{j1},...V_{jk}$不会延期。
也就是有这样一个式子$$VLleft[ i ight] =min left( VLleft[ j_{p} ight] -lengthleft[ r_{p} ight] ight), p=1,2,...,k$$
跟$VE$数组相类似,如果想要计算出$VL[i]$的正确值,就必须在访问$V_i$之前$VL[j_{1}]....VL[j_{k}]$都已经得到,跟求$VE$数组刚好相反,也就是在访问某个结点的时候保证它的后继结点都已经访问完毕了,这就需要用到逆拓扑序列来实现,所以我们上面实现的时候用$Stack$把拓扑序列存了起来。此部分代码如下:
const int inf = 1 << 30; //因为终点一定是关键事件,所以终点的最晚发生时间是等于最早发生时间 VL[n] = VE[n]; fill(VL, VL + n, inf); //上面两句分开写便于理解,这两句可以写成一句fill(VL,VL+n+1,VE[n]); //如果题目默认n是汇点,那么VE[n]就是最长路径,给VL数组赋初值一样可以起到inf的作用 //如果题目没明确说明n是汇点,则遍历一遍求VE的最大值,去代替VE[n]即可 while (!topoOrder.empty()) { int u = topoOrder.top(); topoOrder.pop(); for (int i = 0; i < G[u].size(); i++) { int v = G[u][i].first; VL[u] = min(VL[u], VL[v] - G[u][i].second); } }
主体代码
最后只需要根据$$E[r]+length[r]=VE[j]\ VL[j]=L[r]+length[r]$$计算出$E_i$和$L_i$,判断是否相等即可,完整代码如下:
const int N = 10000; vector<pair<int, int>>G[N + 5];//后继节点、权值 stack<int>topoOrder; int n, m, inDegree[N + 5], VE[N + 5], VL[N + 5]; //结点编号为1~n void topologicalSort() { queue<int >q; for (int i = 1; i <= n; i++) if (inDegree[i] == 0) { q.push(i); } while (!q.empty()) { int u = q.front(); q.pop(); topoOrder.push(u); for (int i = 0; i < G[u].size(); i++) { int v = G[u][i].first; inDegree[v]--; if (inDegree[v] == 0) { q.push(v); } //用VE[u]来更新u的后继节点 VE[v] = max(VE[u] + G[u][i].second, VE[v]); } } fill(VL, VL + n + 1, VE[n]); while (!topoOrder.empty()) { int u = topoOrder.top(); topoOrder.pop(); for (int i = 0; i < G[u].size(); i++) { int v = G[u][i].first; VL[u] = min(VL[u], VL[v] - G[u][i].second); } } for (int u = 1; u <= n; u++) { for (int i = 0; i < G[u].size(); i++) { int v = G[u][i].first, d = G[u][i].second; if (VE[u] == VL[v] - d ) { //u-->v是一条关键路径 } } } }
例题
求关键路径长度
http://acm.hdu.edu.cn/showproblem.php?pid=4109
这题只要求关键路径长度,不要求列举出来,那就只要把VE数组求出来即可

#include <iostream> #include <fstream> #include <algorithm> #include <queue> #include <stack> #include <stdio.h> #include <vector> using namespace std; const int N = 1000; vector<pair<int, int>>G[N + 5];//后继节点、权值 int n, m, inDegree[N + 5], VE[N + 5], VL[N + 5]; void topologicalSort() { queue<int >q; for (int i = 0; i < n; i++) if (inDegree[i] == 0) { q.push(i); } while (!q.empty()) { int u = q.front(); q.pop(); for (int i = 0; i < G[u].size(); i++) { int v = G[u][i].first; inDegree[v]--; if (inDegree[v] == 0) { q.push(v); } //用VE[u]来更新u的后继节点 VE[v] = max(VE[u] + G[u][i].second, VE[v]); } } } int main() { #ifdef LOCAL fstream cin("data.in"); #endif // LOCAL //while (cin >> n >> m) { while (scanf("%d%d", &n, &m) != EOF) { for (int i = 0; i < n; i++) { G[i].clear(); VE[i] = inDegree[i] = 0; } for (int i = 0; i < m; i++) { int c1, c2, c3; scanf("%d%d%d", &c1, &c2, &c3); //cin >> c1 >> c2 >> c3; G[c1].push_back(make_pair(c2, c3)); inDegree[c2]++; } topologicalSort(); //终点不确定,遍历找最大值 int res = 0; for (int i = 0; i < n; i++) { res = max(res, VE[i]); } printf("%d ", res + 1);//按题目意思最小时间为1,所以需要+1 } return 0; }
标准版关键路径
https://acm.sdut.edu.cn/onlinejudge2/index.php/Home/Index/problemdetail/pid/2498.html
最后要求输出字典序最小的关键路径,输出时稍作一点点处理就行了。(题目没有说明,但是数据默认$n$为汇点,交了之后才发现自己写的好像不太对还是过了。。。)

#include <iostream> #include <fstream> #include <algorithm> #include <queue> #include <stack> #include <stdio.h> #include <vector> using namespace std; const int N = 10000; vector<pair<int, int>>G[N + 5];//后继节点、权值 stack<int>topoOrder; int n, m, inDegree[N + 5], VE[N + 5], VL[N + 5]; void topologicalSort() { queue<int >q; for (int i = 1; i <= n; i++) if (inDegree[i] == 0) { q.push(i); } while (!q.empty()) { int u = q.front(); q.pop(); topoOrder.push(u); for (int i = 0; i < G[u].size(); i++) { int v = G[u][i].first; inDegree[v]--; if (inDegree[v] == 0) { q.push(v); } //用VE[u]来更新u的后继节点 VE[v] = max(VE[u] + G[u][i].second, VE[v]); } } //int res = 0; //for (int i = 1; i <= n; i++) { // res = max(res, VE[i]); //} //printf("%d ", res); printf("%d ", VE[n]);//如果题目没说明n就是汇点,这两行的VE[n]都必须改成上面的res fill(VL, VL + n + 1, VE[n]); while (!topoOrder.empty()) { int u = topoOrder.top(); topoOrder.pop(); for (int i = 0; i < G[u].size(); i++) { int v = G[u][i].first; VL[u] = min(VL[u], VL[v] - G[u][i].second); } } int flag = -1; for (int u = 1; u <= n; u++) { for (int i = 0; i < G[u].size(); i++) { int v = G[u][i].first, d = G[u][i].second; if (VE[u] == VL[v] - d && (flag == -1 || u == flag)) { flag = v; cout << u << ' ' << v << endl; } } } } int main() { #ifdef LOCAL fstream cin("data.in"); #endif // LOCAL //while (cin >> n >> m) { while (scanf("%d%d", &n, &m) != EOF) { for (int i = 1; i <= n; i++) { G[i].clear(); VL[i] = VE[i] = inDegree[i] = 0; } for (int i = 0; i < m; i++) { int u, v, w; scanf("%d%d%d", &u, &v, &w); //cin >> u >> v >> w; G[u].push_back({ v, w }); inDegree[v]++; } topologicalSort(); } return 0; } /*************************************************** User name: vsdj Result: Accepted Take time: 52ms Take Memory: 1088KB Submit time: 2019-10-27 16:36:34 ****************************************************/
