数论篇4——逆元（数论倒数）

问题引入

对于取余运算，有一下一些性质：

 

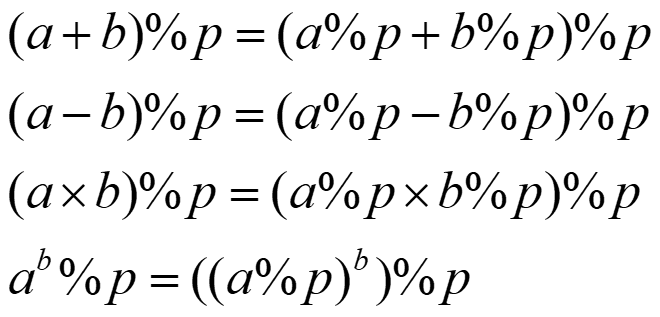
但是唯独除法是不满足的：

 

 为什么除法错的呢？很好证明：

 

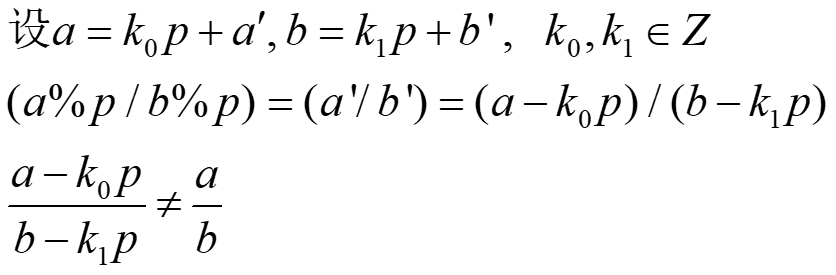
 而对于一些题目，我们必须在中间过程中进行求余，否则数字太大，电脑存不下，那如果这个算式中出现除法，我们就需要逆元了，将除法运算转换为乘法运算。

逆元

定义：

 

对于c，可以说是特殊意义上的倒数，我们可以理解为要求在0,1,2……p-1之间找一个数，是的这个数和a相乘后再取模p，得到的结果为1。

现在就要在回到刚才的问题了，除以一个数等于乘上这个数的倒数，在除法取余的情况下，就是乘上这个数的逆元，即：

 

这样就把除法，完全转换为乘法了。

逆元的性质

唯一性

给定一个数a，若存在模p下的逆元c，c一定唯一。

自反性

c是a的逆元，a也是c的逆元。

逆元的求解

对于逆元的求解，如果n较小的话，是容易算出来的，例如，求3在模26下的逆元：

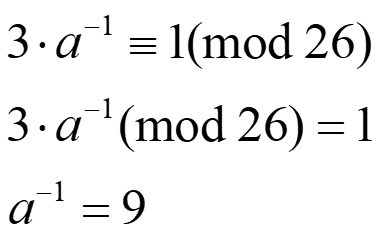
但是当n非常大的时候，手动求解就非常困难了。

扩展欧几里得算法（extend_gcd）

$acdot a^{1}equiv 1(mod b)$

模数可以不为质数，满足gcd(a,b)=1即可

定义：

对于逆元的表达式可以做一些变换：

 

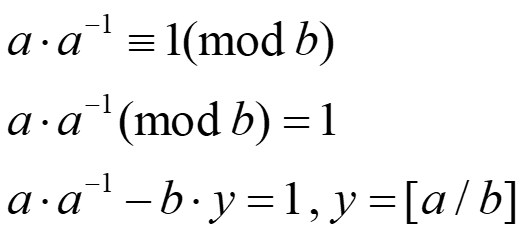
 当gcd(a,b)=1时，代入extend_gcd(a,b,x,y)，得到的非负的x值，就是上面的$a^-1$

int extend_gcd(int a, int b, int& x, int& y) {
    if (b == 0) {
        x = 1, y = 0;
        return a;
    }
    int q = extend_gcd(b, a % b, x, y);
    int temp = x;
    x = y;
    y = temp - a / b * y;
    return q;
}

费马小定理

只适用于模数为质数的情况，如果模数不是质数，可以变换一下，用欧拉定理。

如果p是一个质数，且a不是p的倍数则有 

$a^{p-1}equiv 1(mod p)$

根据同余除法定理，两边同除以a

$a^{p-2}equiv a^{-1}(mod p)$

所以

 $a^{-1}= a^{p-2}(mod p)$

用快速幂求一下，复杂度O(logn)

线性递推

只适用于模数为质数的情况

当p为质数时有$$a^{-1}=(p-[p/a])cdot (p\%a)^{-1}\%p$$

证明：

 

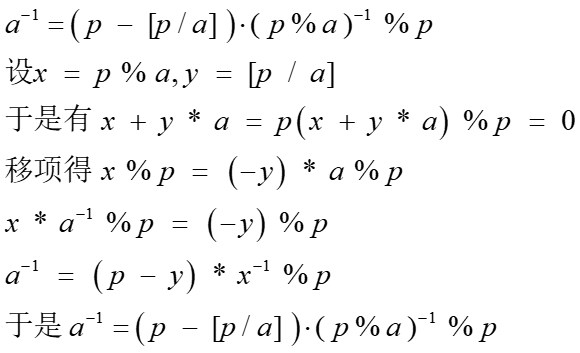
1的逆元就是1，这个方法复杂度是$O(n)$，但并不是说比前两个差，它可以在O(n)的复杂度内算出n个数的逆元。

inv[1] = 1;
for(int i = 2; i < p; ++ i)
    inv[i] = (p - p / i) * inv[p % i] % p;

阶乘递推求逆元

只适用于模数为质数的情况

设 $f(i)=inv(i !)$

则根据：$f(i-1)=frac{1}{ (i-1) !}=frac{1}{i !} imes i =f(i) imes i$

有：$f(i-1) = f(i) imes i$

假设要求 $[1,n]$ 中所有数的逆元，先求得 $[1,n]$ 中所有数的阶乘

可以用 费马小定理 求得 $f(n)$ 的值，之后递推出 $f(1 sim n)$ 的值

但是 $inv(1! sim n! )$ 并不是我们想要的答案，需要继续转化。

根据：$inv(i)=frac{1}{i}=frac{1}{i !} imes (i-1) ! = inv(i!) imes (i-1)!$

最终的转换式 :$$inv(i) = inv(i!) imes(i-1) ! $$

时间复杂度也是$O(n)$

    int N,P;
    fact[0] = 1;
    //mod P 求阶乘
    for (int i = 1; i <= N; i++) 
        fact[i] = fact[i - 1] * i % P;
    //求N! mod p的逆元
    inv[N] = quickPower(fact[N], P - 2, P) % P;
    //递推求N!~1! mod p的逆元
    for (int i = N - 1; i >= 1; i--)
        inv[i] = inv[i + 1] * (i + 1) % P;
    //转换输出
    for (int i = 1; i <= N; i++) 
        printf("%d
", (inv[i] * fact[i - 1]) % P); 

 逆元的应用

费这么大周章求出来的逆元究竟有什么用呢？

将除法转换为乘法

已知$n$为任意整数，$(a,p)=1$，则$ndiv a mod p = ncdot a^{-1} mod p$，

比如 $12div 4 mod 7 = 12cdot 2 mod 7=3$。

具体使用情况就可以是上面提到的，一个取余运算式中间出现了除号。

但如果式子中没有取余呢？那自己取一个呗，取一个特别大的素数（但是不能太大，推荐取1e9+7，好记，快速幂也不会爆long long范围，可以运算所有int范围的数据）

测试代码：

const LL P = 1e9 + 7;

LL quickPower(LL a, LL n, LL p) {
    LL res = 1;
    while (n) {
        if (n & 1) {
            res = (res % p * a % p) % p;
        }
        a = (a % p * a % p) % p;
        n >>= 1;
    }
    return res;
}

int main() {
    LL _a = quickPower(8, P - 2, P);
    LL res = (72 * _a) % P;
    cout << res << endl;
    return 0;
}

注意以下几点：

• 如果真的要计算的数字特别大，可能需要考虑使用快速乘（龟速乘）。
• 要注意实际是否会出现除不尽的情况，因为分数取模比较特殊，算出来的结果不是你想要的答案。
• 具体使用看情况吧，俺还没遇见过。。。