(如果看不到图片,可以右键图 在新标签中打开,再在新打开的标签中右键图 在新标签中打开,然后回来不停刷新博文页面)
导数的运算
![]()
![]()
![]()
y=f(x)的反函数是x=g(y), 则有y'=1/x'.
|
|
|
积分
泰勒中值定理
泰勒公式转换
泰勒公式应用
已经知道了一个函数 G(z),求一个多项式 F(z) (%z^n下),满足方程
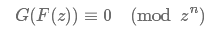
现在假设已经求出了
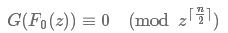
则可用牛顿迭代法推出

再把这个应用到别的多项式问题,用途就很广了。
以下举例 , 可以用这个通式推得的 " 求exp[A(x)]" :
定义:A,B,G为模x^n意义下的多项式,
已知A, 且已用牛顿迭代法在前一层中求出了G(% x^(n/2)下),求B
exp[A(x)] 复杂度O(n·log(n))
求B=e^A (%x^n)
ln[A(x)] 复杂度O(n·log(n))
ln(A)=∫(ln(A))'=∫(A'/A). (%x^n)



组合数有用的公式:
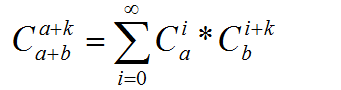


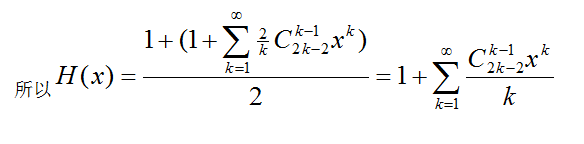
上面那个 是 下标从1开始的卡特兰数,
另一个从0开始的也是一样的,
就是 fn=f0*fn-1+f1*fn-2+……+fn-1*f0
这样的fn实际上就是原来的hn+1
对应的问题 比如说 1~n依次入栈,问出栈顺序有几种。即fn。

(每次把一个元素自成一个轮换,或放在之前的任何一个元素右边)

另一种O(m)计算方法: (考虑容斥)
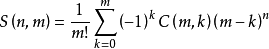
两种斯特林数相关的公式:
第一类斯特林数: 
第二类斯特林数: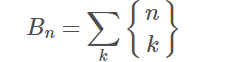 对应贝尔数
对应贝尔数
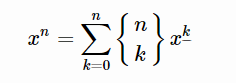
用x种颜色为n个点染色,方案数显然是x^n;但是我们也可以用另外一个方法表示,那就是枚举同种颜色的集合是什么(斯特林子集数),然后从x个颜色里选出不同的颜色赋给这些集合(下降幂)。
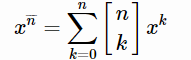
用n颗珠子串成若干串项链,其中每串项链上珠子的颜色必须相同,那么我们就可以枚举项链的组成(第一类斯特林数),然后统一给每串项链分配颜色(x^k);如果用另外一种方法表示的话,我们考虑按照编号从小到大加入每个珠子,每个珠子可以选择在x种颜色里面选一种并且自己成为一串新的项链,也可以选择接在之前某个珠子后面并继承一样的颜色,那么我们的操作方案数是 x的n次上升幂
下降幂: a^b = a*(a-1)*(a-2)*...*(a-b+1)
a^b = a! / (a-b)! = C(a,b) * b!
已经有 a^k = ∑x=0~kS(k,x)*a^x
得出 ∑i=0~n i^k = ∑i=0~n ∑x=0~k S(k,x)*i^x
又有 ∑i=0~ni^k = k! * ∑i=0~n C(i,k) = k! * C(n+1,k+1) = (n+1)^(k+1) /(k+1)
伯努利数
伯努利数满足条件
这是伯努利数的O(n^2)递推。另外 ,伯努利数的 生成函数是 x/(e^x-1)。所以也有nlog(n)的多项式求逆 递推。
利用伯努利数可以求自然数幂和
当k不为0时: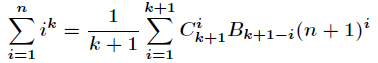
预处理完伯努利数后,单次询问是O(k)的。
证明可以看康复计划,找到的唯一简洁易懂的博客啊。
