1、本节重点知识点用自己的话总结出来,可以配上图片,以及说明该知识点的重要性
(一)回归的分类和定义
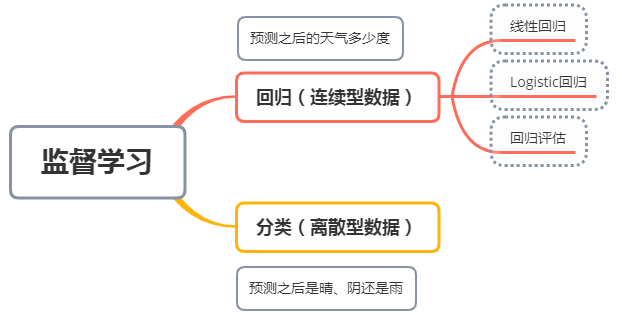

定义:线性回归通过一个或多个自变量与因变量之间进行建模的回归方法,其中可以为一个或多个自变量之间的线性组合。

(二)线性回归的公式
当为一个变量时:

给定一些数据d,并且认为自变量x和因变量y直接存在一定的关系,
可以得到很多的函数集f,其中当a是合适的斜率,b是合适截距时,
这个函数f是最合适用来描述给定数据d中自变量与因变量关系的。


(三)损失函数和最小二乘法
但是y这条线不一定都经过给定的数据点,与实际的数据有偏差,因此会造成一定的损失,引入了损失函数,目的是将损失值减到最小。
损失函数:
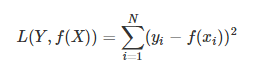
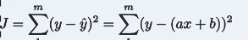

m是数据点的个数
y是真实值,(ax+b)是预测值,其相减的值再平方是最小二乘法。
目标是找到系数a,b,使得损失函数尽可能的小。
当所有误差的平方和相加,得到的最小值,则损失最少,这个时候的a和b就是最合适的斜率和截距。
(四)梯度下降法

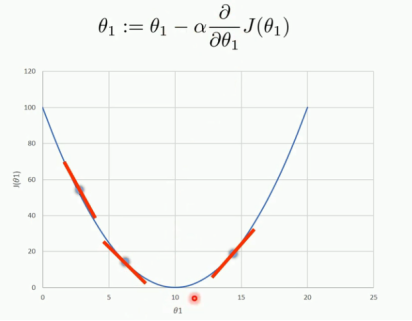
不断下降,得到全局最小值的一个近似值。所以对a(theta1),b(theta0)求最小的偏导数时:
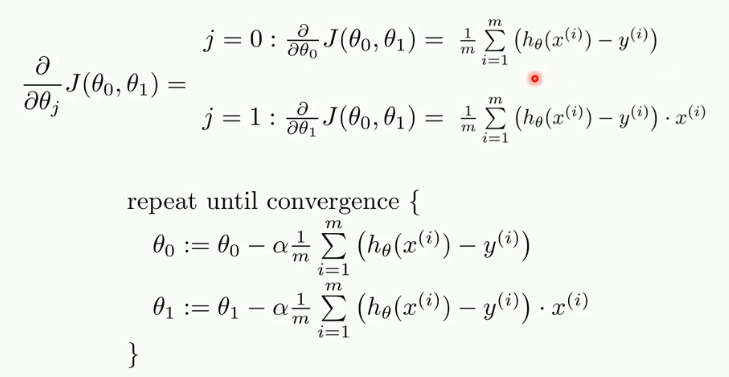
2.思考线性回归算法可以用来做什么?(大家尽量不要写重复)
在自动驾驶碰到障碍物的时候,根据障碍物的大小,障碍物的位置等等特征,预测轮子需要转动的角度是多少。
当电影上映后,可以根据其演员,评分等等对电影票房的预测。
3.自主编写线性回归算法 ,数据可以自己造,或者从网上获取。(加分题)
(一)编码实现线性回归算法
# 核心公式:y=wx+b import numpy as np import matplotlib.pyplot as plt #创建一个矩阵 data=np.array([ [0.067732,3.176513],[0.427810,3.816464],[0.995731,4.550095],[0.738336,4.256571],[0.981083,4.560815], [0.526171,3.929515],[0.378887,3.526170],[0.033859,3.156393],[0.132791,3.110301],[0.138306,3.149813], [0.247809,3.476346],[0.648270,4.119688],[0.731209,4.282233],[0.236833,3.486582],[0.969788,4.655492], [0.607492,3.965162],[0.358622,3.514900],[0.147846,3.125947],[0.637820,4.094115],[0.230372,3.476039], [0.070237,3.210610],[0.067154,3.190612],[0.925577,4.631504],[0.717733,4.295890],[0.015371,3.085028], [0.335070,3.448080],[0.040486,3.167440],[0.212575,3.364266],[0.617218,3.993482],[0.541196,3.891471] ]) x1=data[:,0] #取第一列数据作为x y1=data[:,1] #取第二列数据作为y plt.scatter(x1,y1,marker="o",color="red") plt.show() # 上面是载入数据并且画出数据的散点图 k=0 #斜率 b=0 #截距 iterations=500#迭代多少次 lr=0.05 #学习率 # 最小二乘法 def mincf(b,k,x_data,y_data): total=0 for i in range(len(x_data)): total=total+(y_data[i]-(k*x_data[i]+b))**2 #(y-(kx+b))**2 return total #线性回归算法 def linearhuigui(x_data,y_data,b,k,lr,iterations): m=float(len(x_data)) #数据个数 for i in range(iterations): #数据训练迭代次数 k_grad=0 b_grad=0 # 计算梯度总和再求平均 y=kx+b for j in range(len(x_data)): k_grad+=(1/m)*x_data[j]*(((k*x_data[j])+b)-y_data[j]) #(预测值-实际值)*x的实际值 b_grad+=-(1/m)*(y_data[j]-(k*x_data[j]+b)) #实际值-预测值 #更新b和k b=b-(lr*b_grad) k=k-(lr*k_grad) return b,k print("b={0},k={1},error={2}".format(b,k,mincf(b,k,x1,y1))) b,k=linearhuigui(x1,y1,b,k,lr,iterations) print("经过{0}次迭代后,b={1},k={2},error={3}".format(iterations,b,k,mincf(b,k,x1,y1))) #error是损失值 #画图 plt.scatter(x1,y1) plt.plot(x1,k*x1+b,'r') plt.show()
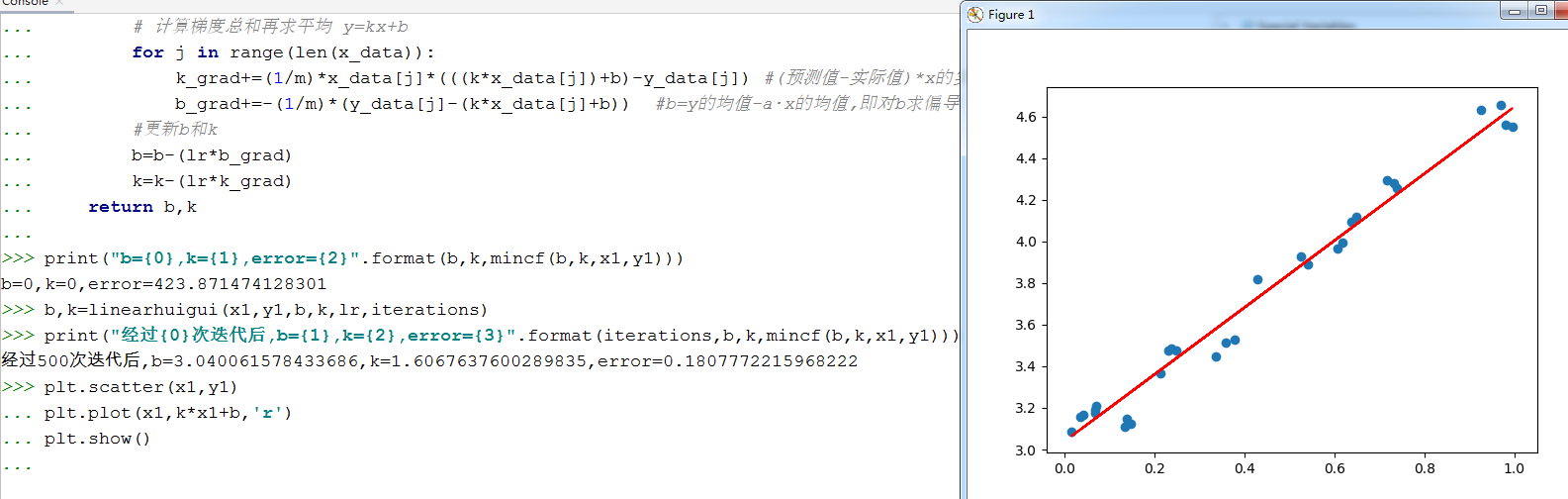
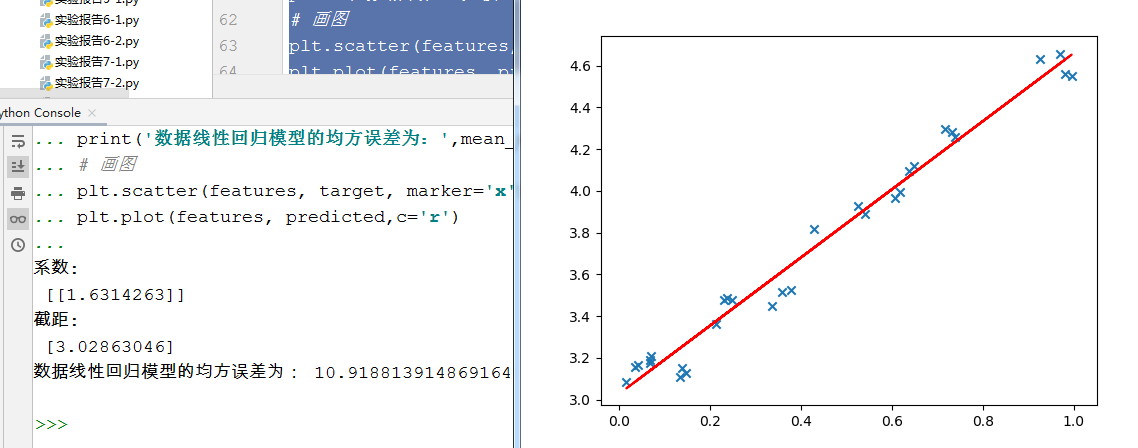
(二)直接使用sklearn的线性回归模型
from sklearn.linear_model import LinearRegression features=data[:,0].reshape(-1,1) target=data[:,1].reshape(-1,1) regression=LinearRegression() #构建模型 model=regression.fit(features,target) #模型训练 predicted = model.predict(features) #预测模型 print('系数: ',model.coef_) print('截距: ',model.intercept_) from sklearn.metrics import mean_squared_error #线性回归模型计算均方误差 print('数据线性回归模型的均方误差为:',mean_squared_error(features,target)) # 画图 plt.scatter(features, target, marker='x') plt.plot(features, predicted,c='r')