Evanyou Blog 彩带

　　题目传送门

平衡点/吊打XXX

题目描述

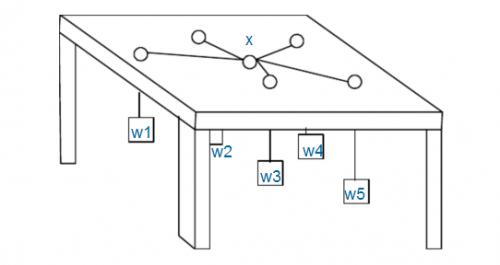
如图：有n个重物，每个重物系在一条足够长的绳子上。每条绳子自上而下穿过桌面上的洞，然后系在一起。图中X处就是公共的绳结。假设绳子是完全弹性的（不会造成能量损失），桌子足够高（因而重物不会垂到地上），且忽略所有的摩擦。

问绳结X最终平衡于何处。

注意：桌面上的洞都比绳结X小得多，所以即使某个重物特别重，绳结X也不可能穿过桌面上的洞掉下来，最多是卡在某个洞口处。

输入输出格式

输入格式：

 

文件的第一行为一个正整数n（1≤n≤1000），表示重物和洞的数目。接下来的n行，每行是3个整数：Xi.Yi.Wi，分别表示第i个洞的坐标以及第 i个重物的重量。(-10000≤x,y≤10000, 0<w≤1000 )

 

输出格式：

 

你的程序必须输出两个浮点数（保留小数点后三位），分别表示处于最终平衡状态时绳结X的横坐标和纵坐标。两个数以一个空格隔开。

 

输入输出样例

输入样例#1： 

3
0 0 1
0 2 1
1 1 1

输出样例#1： 

0.577 1.000

说明

[JSOI]

---

　　分析：

　　正解并不是模拟退火，但是一道练模拟退火的好题。（正解貌似是计算几何+模拟+物理推导？）

　　然后打了个模拟退火，结果交的时候想起来忘了打随机种子，但是已经交了，结果居然A了？？(O.O）然后加上随机种子居然T了？？调了下参然后又WA了？？整了半天总算又A了。不得不说模拟退火这东西是真 · 玄学。。。

　　Code：

//It is made by HolseLee on 19th July 2018
//Luogu.org P1337
#include<bits/stdc++.h>
using namespace std;
#define Rand(T) T*((rand()<<1)-RAND_MAX)
const int N=1e3+7;
const double eps=1e-15;
int n;
struct Point{
    double x,y,w;
}a[N];
double Avex,Avey;
inline double get(double x,double y)
{
    double ret=0;
    for(int i=1;i<=n;i++)
    ret+=sqrt((x-a[i].x)*(x-a[i].x)+(y-a[i].y)*(y-a[i].y))*a[i].w;
    return ret;
}
int main()
{
    srand(19260817);scanf("%d",&n);
    for(int i=1;i<=n;i++){
    scanf("%lf%lf%lf",&a[i].x,&a[i].y,&a[i].w);
    Avex+=a[i].x,Avey+=a[i].y;}
    Avex/=n;Avey/=n;
    double Ans=get(Avex,Avey),Ansx=Avex,Ansy=Avey;
    double delta=0.98;
    for(int i=1;i<=25;i++){
        double Now=get(Avex,Avey),Nowx=Avex,Nowy=Avey; 
        for(double T=201314.0;T>eps;T*=delta){
            double Newx=Nowx+Rand(T),Newy=Nowy+Rand(T);
            double New=get(Newx,Newy);
            if(New<Ans)Ans=New,Ansx=Newx,Ansy=Newy;
            if(New<Now||(exp((New-Now)/T)*RAND_MAX<rand()))
            Now=New,Nowx=Newx,Nowy=Newy;
        }
    }
    printf("%.3lf %.3lf",Ansx,Ansy);
    return 0;
}