一、实验目的
掌握基于覆盖理论与基本路径的基本白盒测试方法和实践
二、实验要求
运用逻辑覆盖测试的覆盖准则设计被测程序的测试用例,并运行测试用例检查程序的正确与否,给出程序缺陷小结。
三、实验内容
1) 被测原代码被测源码链接:http://www.cnblogs.com/cyk0674804/p/6591815.html
2)依据覆盖技术,测试用例列表:
程序图:

DD路径图:
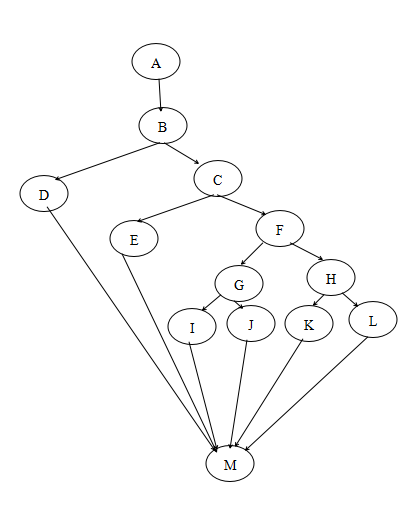
DD-路径(只压缩链路经)
|
程序图节点 |
DD-路径 |
|
1,2 |
A |
|
3 |
B |
|
5 |
C |
|
4,6,9 |
D |
|
7,10,13 |
E |
|
8 |
F |
|
11 |
G |
|
12 |
H |
|
14,18 |
I |
|
15 |
J |
|
16,19,20 |
K |
|
17 |
L |
|
21 |
M |
语句覆盖:
A-B-C-F-H-L-M; A-B-C-F-H-K-M;
A-B-C-F-G-L-M; A-B-C-F-G-K-M;
A-B-C-E-M; A-B-D-M;
测试用例:
|
用例ID |
输入值 |
执行路径 |
预期输出 |
||
|
a |
b |
c |
result |
||
|
1 |
1 |
1 |
1 |
A-B-C-F-H-L-M |
等边三角形 |
|
2 |
8 |
8 |
4 |
A-B-C-F-H-K-M |
等腰三角形 |
|
3 |
3 |
4 |
5 |
A-B-C-F-G-L-M |
直角三角形 |
|
4 |
3 |
4 |
6 |
A-B-C-F-G-K-M |
一般三角形 |
|
5 |
1 |
1 |
8 |
A-B-C-E-M |
不构成三角形 |
|
6 |
111 |
50 |
90 |
A-B-D-M |
边的值不在范围内! |
分支覆盖:
A-B-C-F-H-L-M; A-B-C-F-H-K-M;
A-B-C-F-G-L-M; A-B-C-F-G-K-M;
A-B-C-E-M; A-B-D-M;
测试用例:
|
用例ID |
输入值 |
执行路径 |
预期输出 |
||
|
a |
b |
c |
result |
||
|
1 |
1 |
1 |
1 |
A-B-C-F-H-L-M |
等边三角形 |
|
2 |
8 |
8 |
4 |
A-B-C-F-H-K-M |
等腰三角形 |
|
3 |
3 |
4 |
5 |
A-B-C-F-G-L-M |
直角三角形 |
|
4 |
3 |
4 |
6 |
A-B-C-F-G-K-M |
一般三角形 |
|
5 |
1 |
1 |
8 |
A-B-C-E-M |
不构成三角形 |
|
6 |
111 |
50 |
90 |
A-B-D-M |
边的值不在范围内! |
路径覆盖:
A-B-C-F-H-L-M; A-B-C-F-H-K-M;
A-B-C-F-G-L-M; A-B-C-F-G-K-M;
A-B-C-E-M; A-B-D-M;
测试用例:
|
用例ID |
输入值 |
执行路径 |
预期输出 |
||
|
a |
b |
c |
result |
||
|
1 |
1 |
1 |
1 |
A-B-C-F-H-L-M |
等边三角形 |
|
2 |
8 |
8 |
4 |
A-B-C-F-H-K-M |
等腰三角形 |
|
3 |
3 |
4 |
5 |
A-B-C-F-G-L-M |
直角三角形 |
|
4 |
3 |
4 |
6 |
A-B-C-F-G-K-M |
一般三角形 |
|
5 |
1 |
1 |
8 |
A-B-C-E-M |
不构成三角形 |
|
6 |
111 |
50 |
90 |
A-B-D-M |
边的值不在范围内! |
条件覆盖:
|
编号 |
a>=1 |
a<=100 |
b>=1 |
b<=100 |
c>=1 |
c<=100
|
a>=1 &&a<=100&&b>=1&&b<=100&&c>=1&&c<=100 |
覆盖路径 |
|
1 |
T |
F |
F |
F |
F |
F |
F |
B-C |
|
2 |
T |
T |
F |
F |
F |
F |
F |
B-D |
|
3 |
T |
T |
T |
F |
F |
F |
F |
B-D |
|
4 |
T |
T |
T |
T |
F |
F |
F |
B-D |
|
5 |
T |
T |
T |
T |
T |
F |
F |
B-D |
|
6 |
T |
T |
T |
T |
T |
T |
F |
B-D |
|
7 |
T |
T |
T |
T |
T |
T |
T |
B-C |
|
编号 |
a<b+c |
b<a+c |
c<a+b |
a<b+c &&b<a+c&& c<a+b |
覆盖路径 |
|
1 |
T |
F |
F |
F |
C-E |
|
2 |
T |
T |
F |
F |
C-E |
|
3 |
T |
T |
T |
T |
C-F |
|
4 |
T |
F |
T |
F |
C-E |
|
5 |
F |
F |
F |
F |
C-E |
|
6 |
F |
T |
F |
F |
C-E |
|
7 |
F |
F |
T |
F |
C-E |
|
8 |
F |
T |
T |
F |
C-E |
|
编号 |
a==b |
a==c |
b==c |
a==b || a==c||b==c |
覆盖路径 |
|
1 |
T |
F |
F |
T |
F-H |
|
2 |
T |
T |
F |
T |
F-H |
|
3 |
T |
T |
T |
T |
F-H |
|
4 |
T |
F |
T |
T |
F-H |
|
5 |
F |
F |
F |
F |
F-G |
|
6 |
F |
T |
F |
T |
F-H |
|
7 |
F |
F |
T |
T |
F-H |
|
8 |
F |
T |
T |
T |
F-H |
|
编号 |
a==b |
b==c |
a==b &&b==c |
覆盖路径 |
|
1 |
F |
F |
F |
H-K |
|
2 |
F |
T |
F |
H-K |
|
3 |
T |
F |
F |
H-K |
|
4 |
T |
T |
T |
H-L |
|
编号 |
a*a+b*b==c*c |
b*b+c*c==a*a |
a*a+c*c==b*b |
a*a+b*b==c*c || b*b+c*c==a*a || a*a+c*c==b*b |
覆盖路径 |
|
1 |
T |
F |
F |
T |
G-J |
|
2 |
T |
T |
F |
T |
G-J |
|
3 |
T |
T |
T |
T |
G-J |
|
4 |
T |
F |
T |
T |
G-J |
|
5 |
F |
F |
F |
F |
G-I |
|
6 |
F |
T |
F |
T |
G-J |
|
7 |
F |
F |
T |
T |
G-J |
|
8 |
F |
T |
T |
T |
G-J |
测试用例:
|
用例ID |
输入值 |
执行路径 |
预期输出 |
||
|
a |
b |
c |
result |
||
|
1 |
1 |
1 |
1 |
A-B-C-F-H-L-M |
等边三角形 |
|
2 |
8 |
8 |
4 |
A-B-C-F-H-K-M |
等腰三角形 |
|
3 |
3 |
4 |
5 |
A-B-C-F-G-L-M |
直角三角形 |
|
4 |
3 |
4 |
6 |
A-B-C-F-G-K-M |
一般三角形 |
|
5 |
1 |
1 |
8 |
A-B-C-E-M |
不构成三角形 |
|
6 |
111 |
50 |
90 |
A-B-D-M |
边的值不在范围内! |
Junit测试脚本:
import static org.junit.Assert.*; import org.junit.BeforeClass; import org.junit.Test; public class test01Test { @BeforeClass public static void setUpBeforeClass() throws Exception { } @Test public final void testTriangle() { assertEquals("等边三角形",test01.triangle(1,1,1)); assertEquals("等腰三角形",test01.triangle(8,8,4)); assertEquals("直角三角形",test01.triangle(3,4,5)); assertEquals("一般三角形",test01.triangle(3,4,6)); assertEquals("不构成三角形",test01.triangle(1,1,8)); assertEquals("边的值不在范围内!",test01.triangle(111,50,90)); } }

三、测试小结
代码能够通过所有测试用例,未发现缺陷。
通过本次实验我对白盒测试有了更深刻的理解。进一步掌握了白盒测试的基本路径测试方法,能够更好的设计测试用例。
一个好的平台可以避免许多手工测试的麻烦,效率更加显著。