Solve this interesting problem
Time Limit: 2000/1000 MS (Java/Others) Memory Limit: 32768/32768 K (Java/Others)
Total Submission(s): 1020 Accepted Submission(s): 279
Problem Description
Have you learned something about segment tree? If not, don’t worry, I will explain it for you.
Segment Tree is a kind of binary tree, it can be defined as this:
- For each node u in Segment Tree, u has two values: Lu and Ru.
- If Lu=Ru, u is a leaf node.
- If Lu≠Ru, u has two children x and y,with Lx=Lu,Rx=⌊Lu+Ru2⌋,Ly=⌊Lu+Ru2⌋+1,Ry=Ru.
Here is an example of segment tree to do range query of sum.
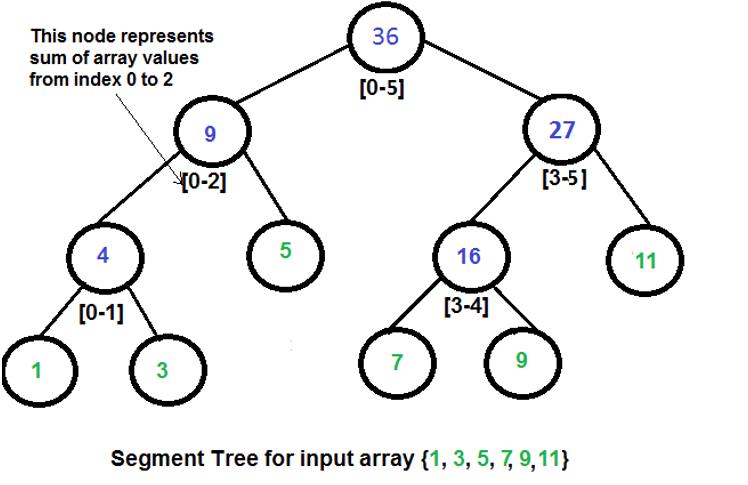
Given two integers L and R, Your task is to find the minimum non-negative n satisfy that: A Segment Tree with root node's value Lroot=0 and Rroot=ncontains a node u with Lu=L and Ru=R.
Segment Tree is a kind of binary tree, it can be defined as this:
- For each node u in Segment Tree, u has two values: Lu and Ru.
- If Lu=Ru, u is a leaf node.
- If Lu≠Ru, u has two children x and y,with Lx=Lu,Rx=⌊Lu+Ru2⌋,Ly=⌊Lu+Ru2⌋+1,Ry=Ru.
Here is an example of segment tree to do range query of sum.

Given two integers L and R, Your task is to find the minimum non-negative n satisfy that: A Segment Tree with root node's value Lroot=0 and Rroot=ncontains a node u with Lu=L and Ru=R.
Input
The input consists of several test cases.
Each test case contains two integers L and R, as described above.
0≤L≤R≤109
LR−L+1≤2015
Each test case contains two integers L and R, as described above.
0≤L≤R≤109
LR−L+1≤2015
Output
For each test, output one line contains one integer. If there is no such n, just output -1.
Sample Input
6 7
10 13
10 11
Sample Output
7
-1
12
Source
Recommend

1 #include <stdio.h> 2 #include <string.h> 3 #include <assert.h> 4 #include <algorithm> 5 const long long inf=(long long) 1e30; 6 7 long long n; 8 9 /*int look(int x) 10 { 11 if(x%2==0) 12 return 2; 13 else 14 return 1; 15 }*/ 16 17 void dfs(long long l,long long r) 18 { 19 if(l<0 || r>inf) 20 return; 21 if(l==0) 22 { 23 if(r<n) 24 n=r; 25 return ; 26 } 27 if(l<r-l+1) 28 return; 29 if(r-l+1!=1) 30 dfs(l,r+(r-l+1)-1); 31 dfs(l-(r-l+1),r); 32 dfs(l-(r-l+1)-1,r); 33 dfs(l,r+(r-l+1)); 34 return; 35 } 36 37 int main() 38 { 39 int L,R; 40 while(scanf("%d %d",&L,&R)!=EOF) 41 { 42 assert(0 <= L && L <= (int)1e9); 43 assert(0 <= R && R <= (int)1e9); 44 assert(L <= R); 45 assert(L / (R - L + 1) <= 2015); 46 n=inf; 47 dfs((long long) L,(long long) R); 48 if(n==inf) 49 printf("-1 "); 50 else 51 printf("%I64d ",n); 52 } 53 return 0; 54 }
