同余最短路在我们做题中很少出现,是属于比较冷门的一种算法。当题目中出现例如“给定m个整数,求这m个整数能拼凑出多少的其他整数(这m个整数可以重复取)”,以及“给定m个整数,求这m个整数不能拼凑出的最小(最大)的整数”的话时我们可以考虑同余最短路的方法。
例1:P3403 跳楼机
-
我们考虑操作2和操作3 (mod) (x)能到达的楼层,可以发现最终答案一定落在(x)的剩余系内。当我们知道这些合法的剩余系的时候,就可以不断累加(x)的值直到最大高度来求出可以到达的不同高度。
-
如何求出只用操作2,3在每个剩余系到达的最小高度?设(g(k))表示在(x)的剩余系内到达的楼层,如果此时加上操作2,3那么可以得出:
-
那么怎么求出由底层(k=0)到其他剩余系中元素的最小代价呢?最短路可以方便地解决这个问题[1]:构建始点为(k),终点为((k+y)modx)且长度为(y)的边,最后从节点0跑最短路就可以了。对于操作3也是如此,同样一起建边。(初始化dist[0]=1)
-
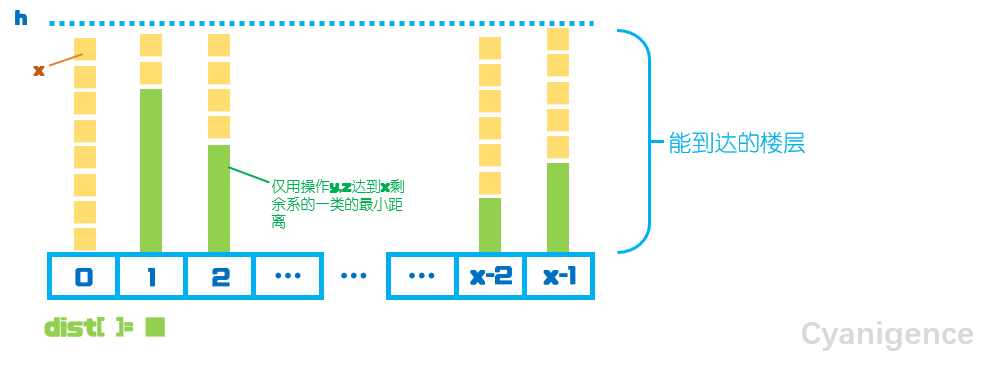
现在我们已经求出(dist[])数组,内部存储了仅使用操作2,3到该节点需要的最小代价(即到达的最小楼层)。最后需要求出用操作1能到达的楼层数,扫描(x)中的剩余系,代入公式:(ans+=(h-dist[i])/x+1)就能得出最终答案。
示意图:
Code:
#include<bits/stdc++.h>
#define ll long long
#define INF 0x3f3f3f3f
#define N 1000010
using namespace std;
ll first[N],next[N],go[N],cost[N],tot;
ll dist[N],vis[N],h,x,y,z,ans;
inline void add_edge(ll u,ll v,ll w){
next[++tot]=first[u];
first[u]=tot;
go[tot]=v;
cost[tot]=w;
}
inline void spfa(){
queue<ll>q;
memset(dist,INF,sizeof(dist));
memset(vis,0,sizeof(vis));
dist[0]=1;vis[0]=1;
q.push(0);
while(!q.empty()){
ll u=q.front();q.pop();
vis[u]=0;
for(ll e=first[u];e;e=next[e]){
ll v=go[e],w=cost[e];
if(dist[v]>dist[u]+w){
dist[v]=dist[u]+w;
if(!vis[v]){
q.push(v);vis[v]=1;
}
}
}
}
}
signed main()
{
scanf("%lld%lld%lld%lld",&h,&x,&y,&z);
if(x==1||y==1||z==1){printf("%d",h);return 0;}//可以直接到任何楼层
for(int i=0;i<=x-1;i++){
add_edge(i,(i+y)%x,y);
add_edge(i,(i+z)%x,z);
}
spfa();
for(int i=0;i<=x-1;i++){
if(dist[i]<=h) ans+=(h-dist[i])/x+1;//统计答案
}
printf("%lld",ans);
return 0;
}
例2:P2662 牛场围栏
-
这道题同样可以用同余最短路解决,
区别是上一道题是紫题,这道题是蓝题(逃。题目要求求出最大不能拼凑出来的木板长度,因此我们把最短的木板作为剩余系,扫描其他的木板并建边。题目另外说每个木板可以最多截掉m米,那么只要再扫描到每个木板的时候依次扫描这个木板能被截成的长度就好了。 -
如何解决不能凑出来的最大木板长度?我们求出的dist[]数组是不使用(a[1]-m)的长度外能凑出来的最小长度,那么只要从dist[]中减去这个值就能得出剩余系中这类不能拼凑的最大值。对所有类都进行这样的处理,最终就能得出不能凑出的最大值。
-
此外题目特判任意长度都可以拼成或最大值不存在输出"-1"。先考虑任意长度都能拼成,如果这个木板的长度能被削成1,那么一定可以达到任意长度,对应为
if(a[1]-m<=1)[2]。最大值不存在的情况为剩余系中一类数都无法拼成,即dist[k]没有被松弛。
具体细节详见代码:
#include<bits/stdc++.h>
#define N 2500010
#define INF 0x3f3f3f3f
using namespace std;
int n,m,ans,a[500],dist[N<<1],vis[N<<1],tot;
int first[N],next[N<<1],go[N<<1],cost[N<<1];
inline void add_edge(int u,int v,int w){
next[++tot]=first[u];
first[u]=tot;
go[tot]=v;
cost[tot]=w;
}
inline void spfa(){
queue<int> q;
memset(dist,INF,sizeof(dist));
memset(vis,0,sizeof(vis));
dist[0]=0;vis[0]=1;
q.push(0);
while(!q.empty()){
int u=q.front();q.pop();
vis[u]=0;
for(int e=first[u];e;e=next[e]){
int v=go[e],w=cost[e];
if(dist[v]>dist[u]+w){
dist[v]=dist[u]+w;
if(!vis[v]){
q.push(v);vis[v]=1;
}
}
}
}
}
int main()
{
scanf("%d%d",&n,&m);
for(int i=1;i<=n;i++) scanf("%d",&a[i]);//木棒长度
sort(a+1,a+n+1);
if(a[1]-m<=1){printf("-1");return 0;}//任意长度都能达到
for(int i=1;i<=n;i++)//扫描每根木棒
for(int j=max(a[i]-m,a[i-1]+1);j<=a[i];j++)//扫描木棒能削出来的长度,其中max()保证不重复
for(int k=0;k<a[1]-m;k++) add_edge(k,(k+j)%(a[1]-m),j);//0~a[1]-1 作为剩余系,操作同例1
spfa();
for(int i=1;i<=a[1]-m-1;i++){
if(dist[i]>100000000){//最大值不存在,mod x=i这一类数全凑不出来
printf("-1");return 0;
}
ans=max(ans,dist[i]-(a[1]-m));
}
printf("%d",ans);
return 0;
}
