问题描述:
给定一个完全无向图G=(V,E),其每一边(u,v)∈E有一非负整数费用c(u,v)。要找出G的最小费用哈密顿回路。
旅行售货员问题的一些特殊性质:
比如,费用函数c往往具有三角不等式性质,即对任意的3个顶点u,v,w∈V,有:c(u,w)≤c(u,v)+c(v,w)。当图G中的顶点就是平面上的点,任意2顶点间的费用就是这2点间的欧氏距离时,费用函数c就具有三角不等式性质。
当费用函数c具有三角不等式性质时,可以设计出一个近似算法,其性能比为2.而对于一般情况下的旅行售货员问题则不可能设计出具有常数性能比的近似算法,除非P=NP.
具有三角不等式性质的旅行售货员问题
对于给定的无向图G,可以利用找图G的最小生成树的算法设计找近似最优的旅行售货员回路的算法。当费用函数满足三角不等式时,算法找出的旅行售货员回路的费用不会超过最优旅行售货员回路费用的2倍。
void approxTSP (Graph g)
{
(1)选择g的任一顶点r;
(2)用Prim算法找出带权图g的一棵以r为根的最小生成树T;
(3)前序遍历树T得到的顶点表L;
(4)将r加到表L的末尾,按表L中顶点次序组成回路H,作为计 算结果返回;
}
下图说明算法approxTSP运行情况:
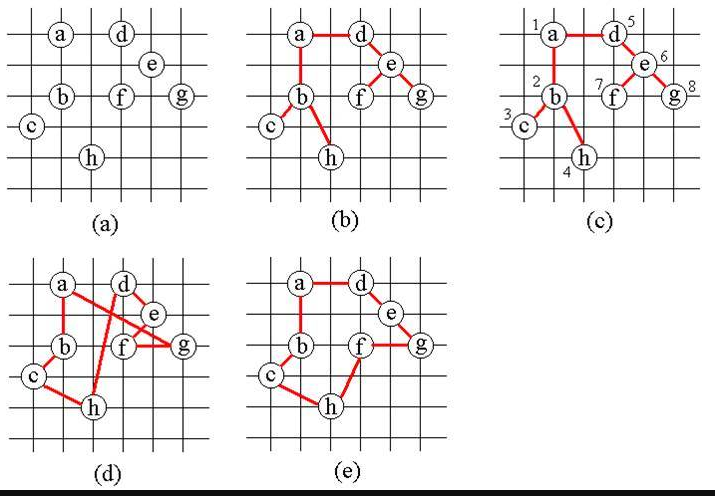
(b)表示找到的最小生成树T;(c)表示对T作前序遍历的次序;(d)表示L产生的哈密顿回路H;(e)是G的一个最小费用旅行售货员回路。
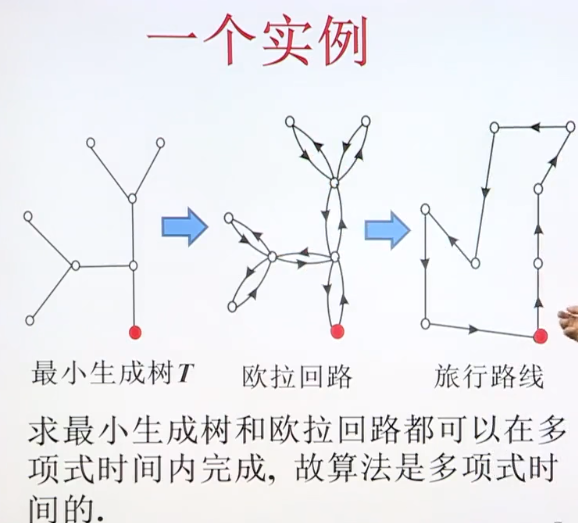
当费用函数满足三角不等式时,该算法具有较好的性能比,即对于无向图G,算法具有常数性能比2.以下参考屈老师课件。






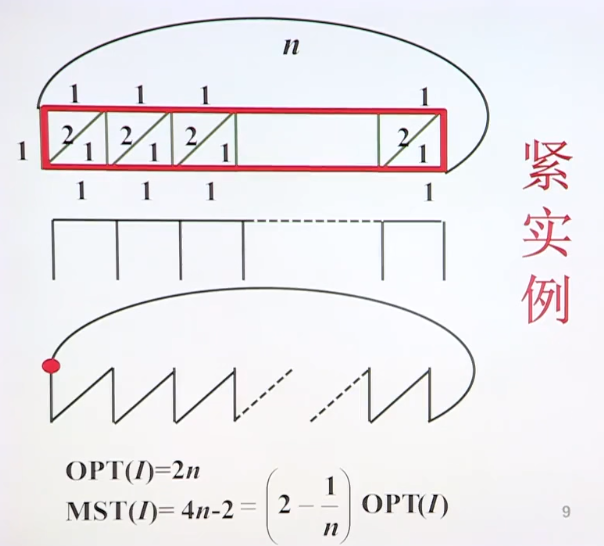



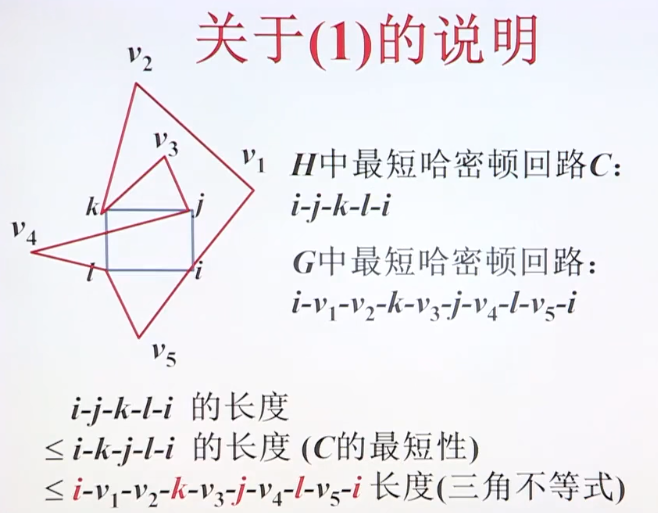





对于一般货郎问题,换句话说,若P≠NP,则对任意常数ρ>1,不存在性能比为ρ的解旅行售货员问题的多项式时间近似算法。
参考:北大《算法设计与分析》公开课(https://www.bilibili.com/video/BV1e4411x7Qj?p=4)
王晓东《算法设计与分析》第二版