说明:本文转载自https://blog.csdn.net/u012102306/article/details/53184446?depth_1-,不过有一说一,写的挺不错,为方便后续学习,所以载入博客
1.基本概念
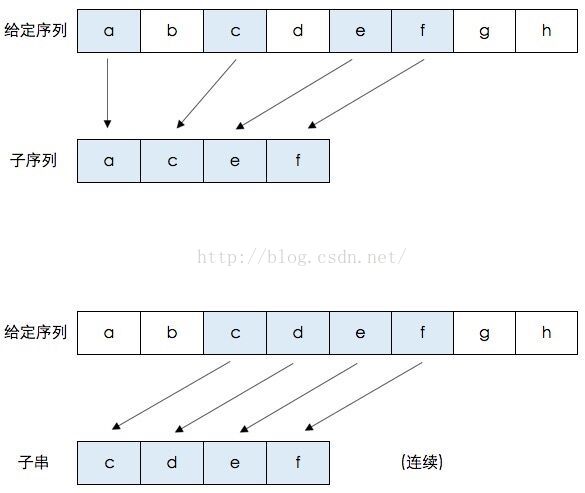
首先需要科普一下,最长公共子序列(longest common sequence)和最长公共子串(longest common substring)不是一回事儿。什么是子序列呢?即一个给定的序列的子序列,就是将给定序列中零个或多个元素去掉之后得到的结果。什么是子串呢?给定串中任意个连续的字符组成的子序列称为该串的子串。给一个图再解释一下:
如上图,给定的字符序列: {a,b,c,d,e,f,g,h},它的子序列示例: {a,c,e,f} 即元素b,d,g,h被去掉后,保持原有的元素序列所得到的结果就是子序列。同理,{a,h},{c,d,e}等都是它的子序列。
它的字串示例:{c,d,e,f} 即连续元素c,d,e,f组成的串是给定序列的字串。同理,{a,b,c,d},{g,h}等都是它的字串。
这个问题说明白后,最长公共子序列(以下都简称LCS)就很好理解了。
给定序列s1={1,3,4,5,6,7,7,8},s2={3,5,7,4,8,6,7,8,2},s1和s2的相同子序列,且该子序列的长度最长,即是LCS。
s1和s2的其中一个最长公共子序列是 {3,4,6,7,8}
2.动态规划
求解LCS问题,不能使用暴力搜索方法。一个长度为n的序列拥有 2的n次方个子序列,它的时间复杂度是指数阶,太恐怖了。解决LCS问题,需要借助动态规划的思想。
动态规划算法通常用于求解具有某种最优性质的问题。在这类问题中,可能会有许多可行解。每一个解都对应于一个值,我们希望找到具有最优值的解。动态规划算法与分治法类似,其基本思想也是将待求解问题分解成若干个子问题,先求解子问题,然后从这些子问题的解得到原问题的解。与分治法不同的是,适合于用动态规划求解的问题,经分解得到子问题往往不是互相独立的。若用分治法来解这类问题,则分解得到的子问题数目太多,有些子问题被重复计算了很多次。如果我们能够保存已解决的子问题的答案,而在需要时再找出已求得的答案,这样就可以避免大量的重复计算,节省时间。我们可以用一个表来记录所有已解的子问题的答案。不管该子问题以后是否被用到,只要它被计算过,就将其结果填入表中。这就是动态规划法的基本思路。
3.特征分析
解决LCS问题,需要把原问题分解成若干个子问题,所以需要刻画LCS的特征。
设A=“a0,a1,…,am”,B=“b0,b1,…,bn”,且Z=“z0,z1,…,zk”为它们的最长公共子序列。不难证明有以下性质:
如果am=bn,则zk=am=bn,且“z0,z1,…,z(k-1)”是“a0,a1,…,a(m-1)”和“b0,b1,…,b(n-1)”的一个最长公共子序列;
如果am!=bn,则若zk!=am,蕴涵“z0,z1,…,zk”是“a0,a1,…,a(m-1)”和“b0,b1,…,bn”的一个最长公共子序列;
如果am!=bn,则若zk!=bn,蕴涵“z0,z1,…,zk”是“a0,a1,…,am”和“b0,b1,…,b(n-1)”的一个最长公共子序列。
有些同学,一看性质就容易晕菜,所以我给出一个图来让这些同学理解一下:
以我在第1小节举的例子(S1={1,3,4,5,6,7,7,8}和S2={3,5,7,4,8,6,7,8,2}),并结合上图来说:
假如S1的最后一个元素 与 S2的最后一个元素相等,那么S1和S2的LCS就等于 {S1减去最后一个元素} 与 {S2减去最后一个元素} 的 LCS 再加上 S1和S2相等的最后一个元素。
假如S1的最后一个元素 与 S2的最后一个元素不等(本例子就是属于这种情况),那么S1和S2的LCS就等于 : {S1减去最后一个元素} 与 S2 的LCS, {S2减去最后一个元素} 与 S1 的LCS 中的最大的那个序列。
4.递归公式
第3节说了LCS的特征,我们可以发现,假设我需要求 a1 ... am 和 b1 .. b(n-1)的LCS 和 a1 ... a(m-1) 和 b1 .. bn的LCS,一定会递归地并且重复地把如a1... a(m-1) 与 b1 ... b(n-1) 的 LCS 计算几次。所以我们需要一个数据结构来记录中间结果,避免重复计算。
假设我们用c[i,j]表示Xi 和 Yj 的LCS的长度(直接保存最长公共子序列的中间结果不现实,需要先借助LCS的长度)。其中X = {x1 ... xm},Y ={y1...yn},Xi = {x1 ... xi},Yj={y1... yj}。可得递归公式如下:
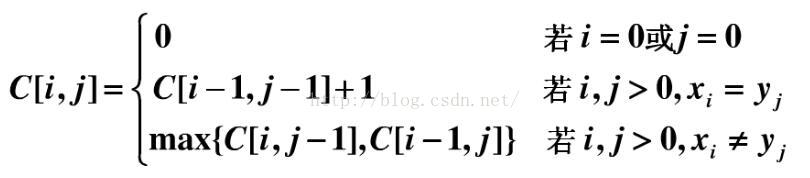
5.计算LCS的长度
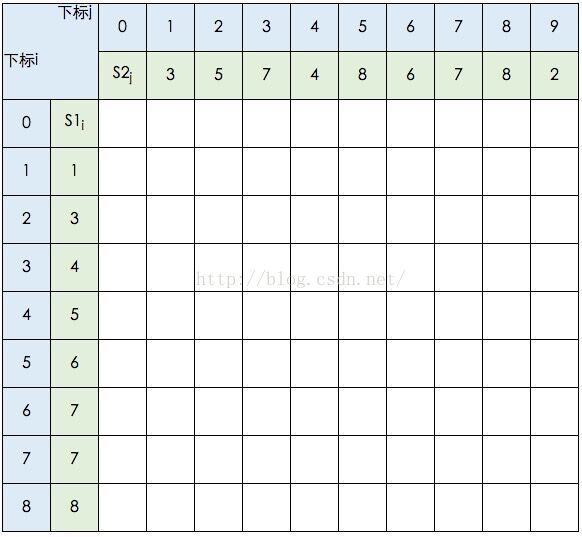
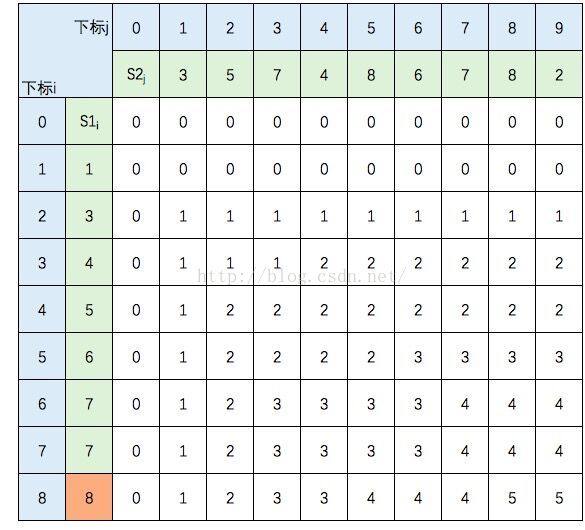
这里我不打算贴出相应的代码,只想把这个过程说明白。还是以s1={1,3,4,5,6,7,7,8},s2={3,5,7,4,8,6,7,8,2}为例。我们借用《算法导论》中的推导图:
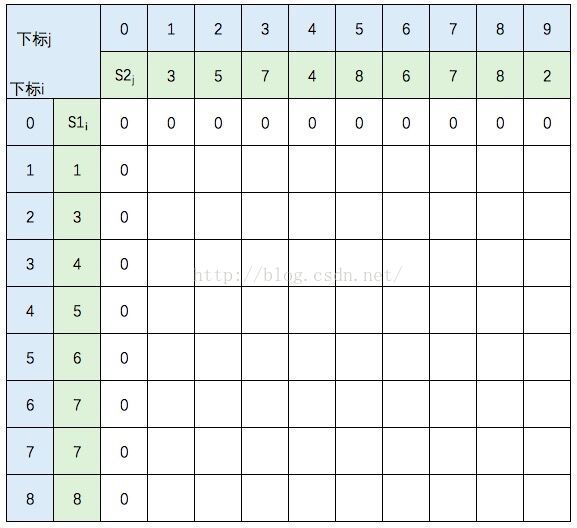
图中的空白格子需要填上相应的数字(这个数字就是c[i,j]的定义,记录的LCS的长度值)。填的规则依据递归公式,简单来说:如果横竖(i,j)对应的两个元素相等,该格子的值 = c[i-1,j-1] + 1。如果不等,取c[i-1,j] 和 c[i,j-1]的最大值。首先初始化该表:
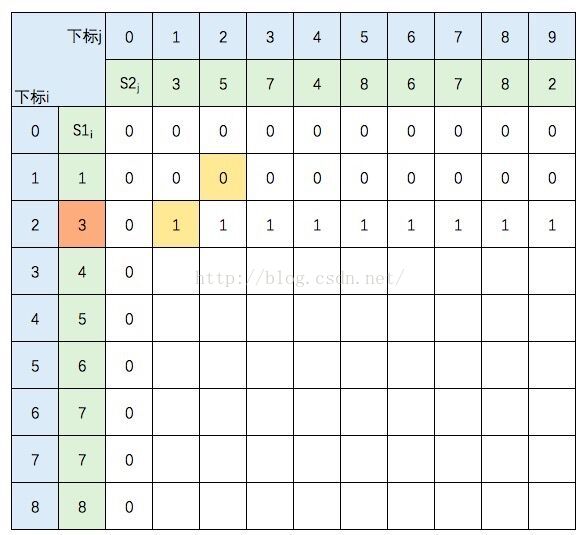
然后,一行一行地从上往下填:
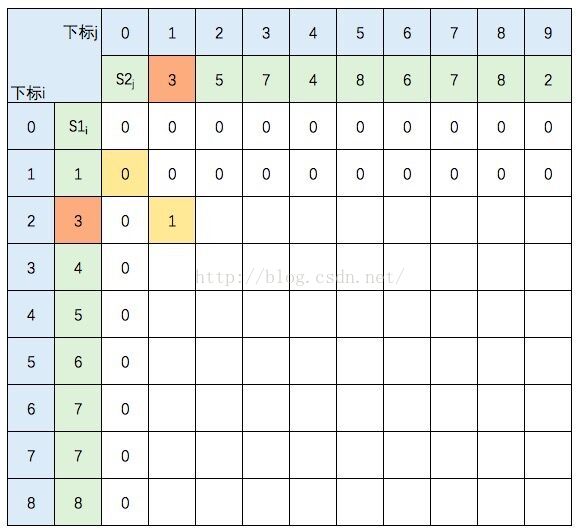
S1的元素3 与 S2的元素3 相等,所以 c[2,1] = c[1,0] + 1。继续填充:
S1的元素3 与 S2的元素5 不等,c[2,2] =max(c[1,2],c[2,1]),图中c[1,2] 和 c[2,1] 背景色为浅黄色。
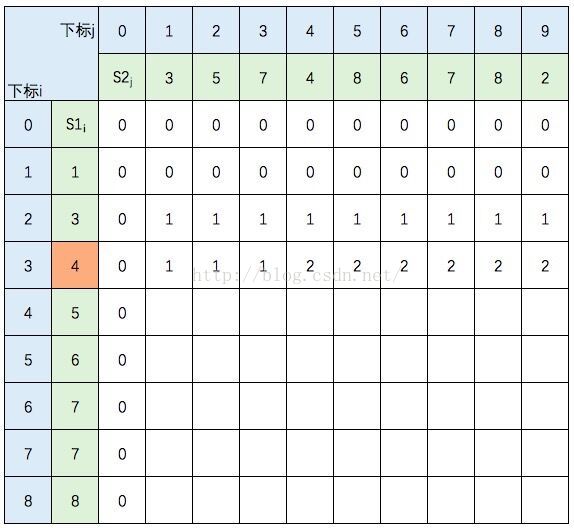
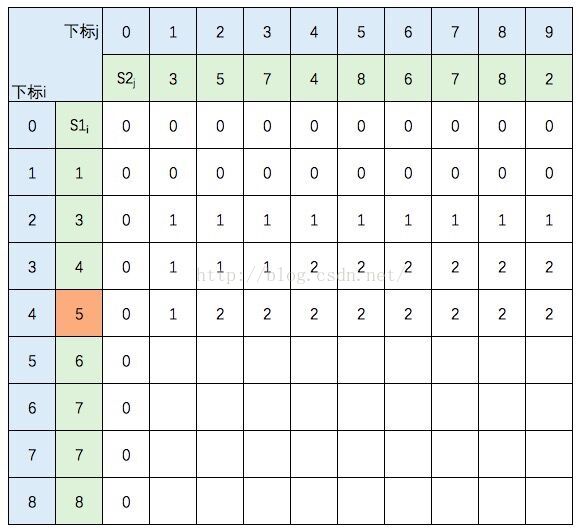
继续填充:
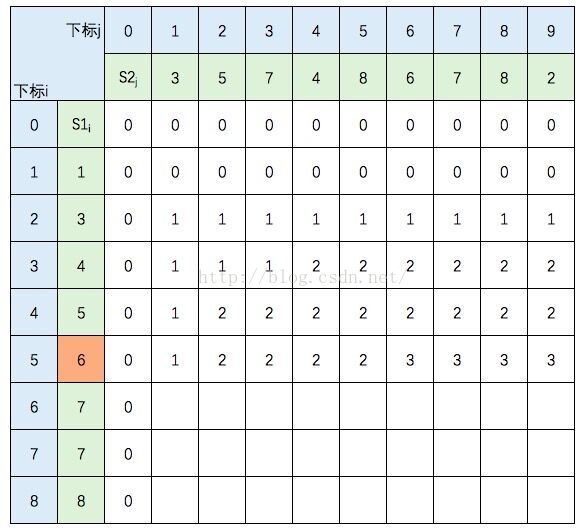
中间几行填写规则不变,直接跳到最后一行:
至此,该表填完。根据性质,c[8,9] = S1 和 S2 的 LCS的长度,即为5。
6.构造LCS
本文S1和S2的最LCS并不是只有1个,本文并不是着重讲输出两个序列的所有LCS,只是介绍如何通过上表,输出其中一个LCS。
我们根据递归公式构建了上表,我们将从最后一个元素c[8][9]倒推出S1和S2的LCS。
c[8][9] = 5,且S1[8] != S2[9],所以倒推回去,c[8][9]的值来源于c[8][8]的值(因为c[8][8] > c[7][9])。
c[8][8] = 5, 且S1[8] = S2[8], 所以倒推回去,c[8][8]的值来源于 c[7][7]。
以此类推,如果遇到S1[i] != S2[j] ,且c[i-1][j] = c[i][j-1] 这种存在分支的情况,这里请都选择一个方向(之后遇到这样的情况,也选择相同的方向)。
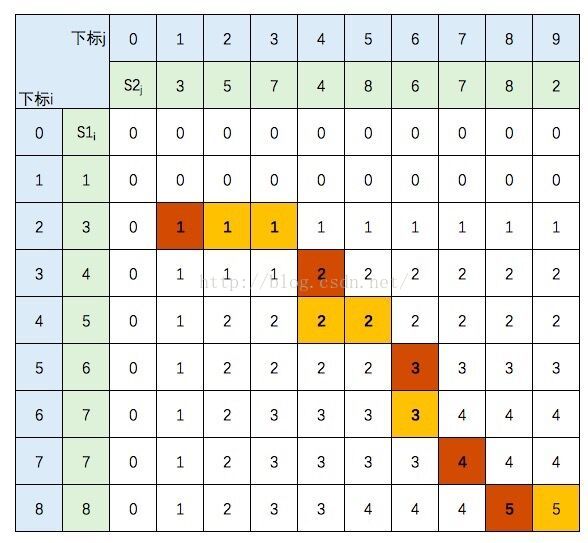
第一种结果为:
这就是倒推回去的路径,棕色方格为相等元素,即LCS = {3,4,6,7,8},这是其中一个结果。
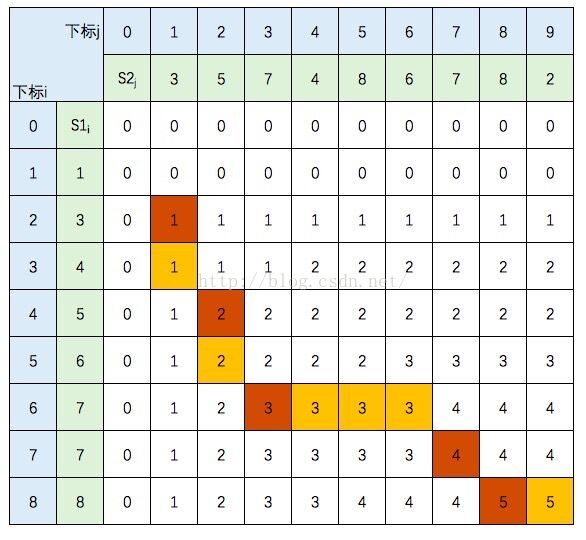
如果遇到S1[i] != S2[j] ,且c[i-1][j] = c[i][j-1] 这种存在分支的情况,选择另一个方向,会得到另一个结果。
即LCS ={3,5,7,7,8}。
7.关于时间复杂度
构建c[i][j]表需要Θ(mn),输出1个LCS的序列需要Θ(m+n)。
8.代码如下:

1 #include <iostream> 2 #include <string> 3 #include <stack> 4 using namespace std; 5 void LCS(string s1,string s2) 6 { 7 int m=s1.length()+1; 8 int n=s2.length()+1; 9 int **c; 10 int **b; 11 c=new int* [m]; 12 b=new int* [m]; 13 for(int i=0;i<m;i++) 14 { 15 c[i]=new int [n]; 16 b[i]=new int [n]; 17 for(int j=0;j<n;j++) 18 b[i][j]=0; 19 } 20 for(int i=0;i<m;i++) 21 c[i][0]=0; 22 for(int i=0;i<n;i++) 23 c[0][i]=0; 24 for(int i=0;i<m-1;i++) 25 { 26 for(int j=0;j<n-1;j++) 27 { 28 if(s1[i]==s2[j]) 29 { 30 c[i+1][j+1]=c[i][j]+1; 31 b[i+1][j+1]=1; //1表示箭头为 左上 32 } 33 else if(c[i][j+1]>=c[i+1][j]) 34 { 35 c[i+1][j+1]=c[i][j+1]; 36 b[i+1][j+1]=2; //2表示箭头向 上 37 } 38 else 39 { 40 c[i+1][j+1]=c[i+1][j]; 41 b[i+1][j+1]=3; //3表示箭头向 左 42 } 43 } 44 } 45 for(int i=0;i<m;i++) //输出c数组 46 { 47 for(int j=0;j<n;j++) 48 { 49 cout<<c[i][j]<<' '; 50 } 51 cout<<endl; 52 } 53 stack<char> same; //存LCS字符 54 stack<int> same1,same2; //存LCS字符在字符串1和字符串2中对应的下标,方便显示出来 55 for(int i = m-1,j = n-1;i >= 0 && j >= 0; ) 56 { 57 if(b[i][j] == 1) 58 { 59 i--; 60 j--; 61 same.push(s1[i]); 62 same1.push(i); 63 same2.push(j); 64 } 65 else if(b[i][j] == 2) 66 i--; 67 else 68 j--; 69 } 70 cout<<s1<<endl; //输出字符串1 71 for(int i=0;i<m && !same1.empty();i++) //输出字符串1的标记 72 { 73 if(i==same1.top()) 74 { 75 cout<<1; 76 same1.pop(); 77 } 78 else 79 cout<<' '; 80 } 81 cout<<endl<<s2<<endl; //输出字符串2 82 for(int i=0;i<n && !same2.empty();i++) //输出字符串2的标记 83 { 84 if(i==same2.top()) 85 { 86 cout<<1; 87 same2.pop(); 88 } 89 else 90 cout<<' '; 91 } 92 cout<<endl<<"最长公共子序列为:"; 93 while(!same.empty()) 94 { 95 cout<<same.top(); 96 same.pop(); 97 } 98 cout<<endl<<"长度为:"<<c[m-1][n-1]<<endl; 99 for (int i = 0; i<m; i++) 100 { 101 delete [] c[i]; 102 delete [] b[i]; 103 } 104 delete []c; 105 delete []b; 106 } 107 int main() 108 { 109 string s1="ABCPDSFJGODIHJOFDIUSHGD"; 110 string s2="OSDIHGKODGHBLKSJBHKAGHI"; 111 LCS(s1,s2); 112 return 0; 113 }
9.运行结果: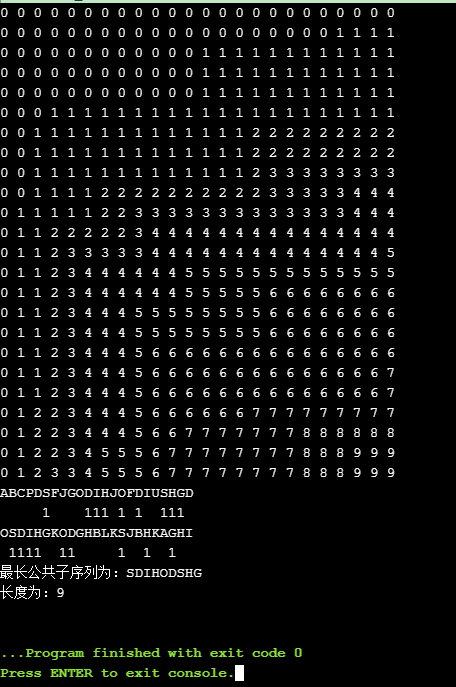
参考:http://baike.baidu.com/link?url=iKrtEZXAQ3LeQLL7Z0HQWpy7EO7BZInUR17C63lAIDFBJ_COm8e3KmKVxQCD6DlOvji2F9W6achz49Z_anZCfa
https://blog.csdn.net/weixin_40673608/article/details/84262695