梯度下降法

1.梯度下降法

是一种基于搜索的最优化方法，作用是最小化一个损失函数。

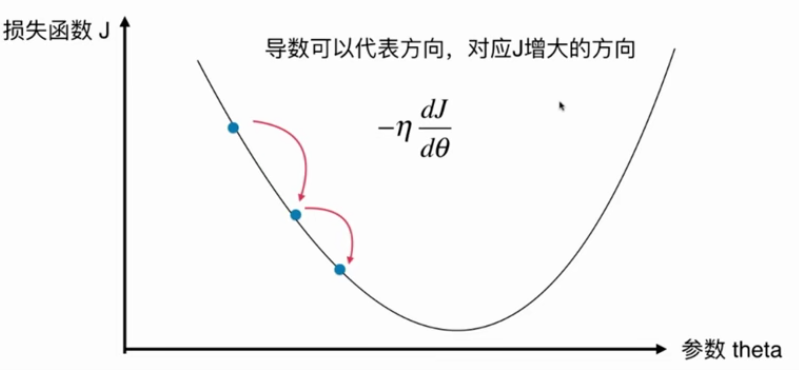
但不是所有的函数都有唯一的极值点。

解决方案：多次运行，随机初始化点

                  梯度下降法的初始点也是一个超参数

线性回归法的损失函数具有唯一的最优解。

模拟实现梯度下降法

import numpy as np
import matplotlib.pyplot as plt

plot_x=np.linspace(-1, 6,141)
plot_y=(plot_x-2.5)**2-1

def dJ(theta):
    return 2*(theta-2.5)

def J(theta):
    try:
        return (theta-2.5)**2-1
    except:
        return float('inf')

#eta为学习速率，n_iters规定最大循环次数
def gradient_descent(initial_theta, eta, n_iters=1e4, epsilon=1e-8):

    theta = initial_theta
    theta_history.append(initial_theta)
    i_iter=0                     #记录当前是第几次循环

    while i_iter<n_iters:
        gradient = dJ(theta)     #计算梯度
        last_theta = theta       #更新theta
        theta = theta - eta * gradient
        theta_history.append(theta)
        
        if (abs(J(theta) - J(last_theta)) < epsilon):
            break
        
        i_iter+=1

def plot_theta_history():
    plt.plot(plot_x, J(plot_x))
    plt.plot(np.array(theta_history),J(np.array(theta_history)),color='r',marker='+')
    plt.show()

eta=0.1
theta_history=[]
gradient_descent(0, eta)
plot_theta_history()

当学习速率eta=0.1和eta=0.8时，相应的图像如下：

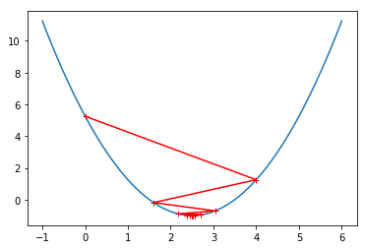
2.线性回归中的梯度下降法

因为多元线性回归的正规方程解复杂度较高，采用梯度下降法解决。

推导如下：

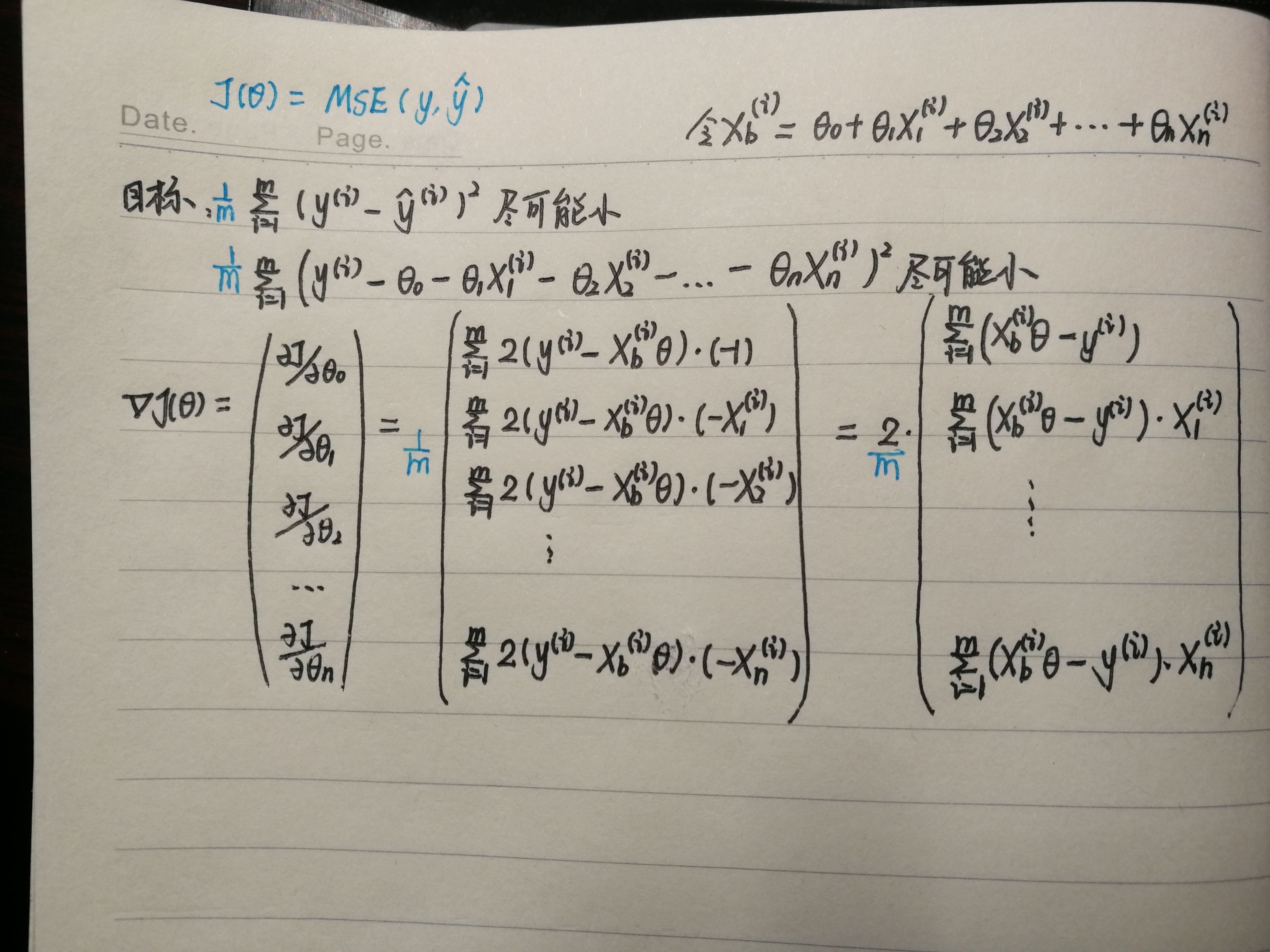
使用梯度下降法求解线性回归参数：

import numpy as np
import matplotlib.pyplot as plt

np.random.seed(666)
x=2*np.random.random(size=100)
y=x*3.+4.+np.random.normal(size=100) #(100,)

X=x.reshape(-1,1)    #(100,1)

plt.scatter(x,y)

def J(theta,X_b,y):
    try:
        return np.sum((y-X_b.dot(theta))**2)/len(X_b)
    except:
        return float('inf')
    
def dJ(theta,X_b,y):
    res=np.empty(len(theta))
    res[0]=np.sum(X_b.dot(theta)-y)
    for i in range(1,len(theta)):
        res[i]=(X_b.dot(theta)-y).dot(X_b[:,i])
        
    return res*2/len(X_b)

def gradient_descent(X_b, y, initial_theta, eta, n_iters=1e4, epsilon=1e-8):
    theta = initial_theta
    cur_iter = 0

    while cur_iter < n_iters:
        gradient = dJ(theta, X_b, y)
        last_theta = theta
        theta = theta - eta * gradient      
        if (abs(J(theta, X_b, y) - J(last_theta, X_b, y)) < epsilon):
            break

    cur_iter += 1
    return theta
 
X_b=np.hstack([np.ones((len(X),1)),X])
initial_theta=np.zeros(X_b.shape[1])
eta=0.01

theta=gradient_descent(X_b, y, initial_theta, eta)
print(theta)      #对应截距和斜率（和调用LinearRegression中的fit函数拟合出的截距和斜率一致）

plt.plot(X,theta[0]+theta[1]*X)
plt.show()

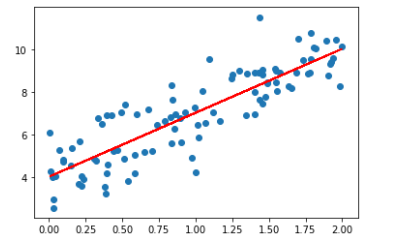
线性回归中梯度下降法的向量化

对上面的推导进行优化：

将上面for循环实现的dJ函数修改如下：

def dJ(theta,X_b,y):
    return X_b.T.dot(X_b.dot(theta)-y)*2.0/len(X_b)

Tip：使用梯度下降之前要进行数据归一化。

3.随机梯度下降法

批量梯度下降法中，每一次计算过程都要将样本中所有信息进行批量计算，如果样本量很大，计算梯度就很耗时。于是引出随机梯度下降法，每次只取一行作为搜索的方向。

eta随着循环次数的增加，学习率降低。

手写随机梯度下降法

import numpy as np

m=100000
x=np.random.normal(size=m)
X=x.reshape(-1,1)   
y=x*4.+3.+np.random.normal(0,3,size=m)
    
def dJ_sgd(theta,X_b_i,y_i):
    return X_b_i.T.dot(X_b_i.dot(theta)-y_i)*2.0

def sgd(X_b, y, initial_theta, n_iters):
    t0=5
    t1=50
    def learning_rate(t):
        return t0/(t+t1)
    
    theta=initial_theta
    for cur_iter in range(n_iters):
        rand_i=np.random.randint(len(X_b))   #随机获得一个索引
        gradient=dJ_sgd(theta, X_b[rand_i], y[rand_i])
        theta=theta-learning_rate(cur_iter)*gradient
    return theta
    
X_b=np.hstack([np.ones((len(X),1)),X])
initial_theta=np.zeros(X_b.shape[1])
eta=0.01

theta=sgd(X_b, y, initial_theta, n_iters=len(X_b)//3)   #只检测了三分之一个样本就可以达到比较好的结果
print(theta)      #对应截距和斜率

scikit-learn中的随机梯度下降法

import numpy as np
from sklearn import datasets

#波士顿房产数据
boston=datasets.load_boston()

X=boston.data    
y=boston.target         

X=X[y<50.0]            #去除掉采集样本拥有的上限点
y=y[y<50.0]

#拆分数据集
from sklearn.model_selection import train_test_split   
X_train,X_test,y_train,y_test=train_test_split(X,y,random_state=666)   

#归一化处理
from sklearn.preprocessing import StandardScaler
standardScaler=StandardScaler()
standardScaler.fit(X_train)

X_train_standard=standardScaler.transform(X_train)             
X_test_standard=standardScaler.transform(X_test)   


from sklearn.linear_model import SGDRegressor
sgd_reg=SGDRegressor(n_iter_no_change=100)             #次数默认为5
sgd_reg.fit(X_train_standard,y_train)
print(sgd_reg.score(X_test_standard,y_test))

4.关于梯度的调试

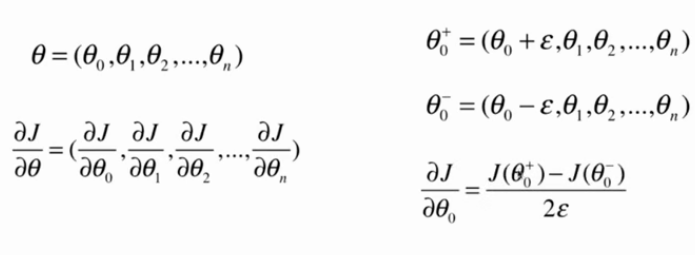
import numpy as np

np.random.seed(666)
X=np.random.random(size=(1000,10))

true_theta=np.arange(1,12,dtype=float)

X_b=np.hstack((np.ones((len(X),1)),X))
y=X_b.dot(true_theta) + np.random.normal(size=1000)

def J(theta,X_b,y):
    try:
        return np.sum((y-X_b.dot(theta))**2)/len(X_b)
    except:
        return float('inf')

#只适用于当前损失函数J（相当于使用了求导公式，所以只适用于当前函数）
def dJ_math(theta,X_b,y):
    return X_b.T.dot(X_b.dot(theta)-y)*2.0/len(y)

#适用于任何损失函数（相当于用定义求导，所以适用于任何函数）
def dJ_debug(theta,X_b,y,epsilon=0.01):
    res=np.empty(len(theta))
    for i in range(len(theta)):
        theta_1=theta.copy()
        theta_1[i]+=epsilon
        
        theta_2=theta.copy()
        theta_2[i]-=epsilon
        res[i]=(J(theta_1,X_b,y)-J(theta_2,X_b,y))/(2*epsilon)
    return res

def gradient_descent(dJ,X_b, y, initial_theta, eta, n_iters=1e4, epsilon=1e-8):
    theta = initial_theta
    cur_iter = 0

    while cur_iter < n_iters:
        gradient = dJ(theta, X_b, y)
        last_theta = theta
        theta = theta - eta * gradient      
        if (abs(J(theta, X_b, y) - J(last_theta, X_b, y)) < epsilon):
            break

    cur_iter += 1
    return theta

initial_theta=np.zeros(X_b.shape[1])
eta=0.01
theta=gradient_descent(dJ_math, X_b, y, initial_theta, eta)
print(theta)

theta=gradient_descent(dJ_debug, X_b, y, initial_theta, eta)
print(theta)

dJ_debug方法比dJ_math方法要慢得多，通过这个方式可以先得到正确的结果，然后再推导公式求解梯度公式的数学解，最后将解和debug的解比较，从而判断我们推导的公式是否正确。