线性回归法

1.最小二乘法

手工推导使损失函数最小的参数a和b：

2.简单线性回归的实现

import numpy as np
import matplotlib.pyplot as plt

x=np.array([1.,2.,3.,4.,5.])
y=np.array([1.,3.,2.,3.,5.])

#根据公式计算参数a和b
x_mean,y_mean=np.mean(x),np.mean(y)
num=0.0
d=0.0
for x_i,y_i in zip(x,y):
    num+=(x_i-x_mean)*(y_i-y_mean)
    d+=(x_i-x_mean)**2
a=num/d
b=y_mean-a*x_mean
print(a,b)

#根据a和b，画出直线
y_hat=a*x+b
plt.scatter(x,y)
plt.plot(x,y_hat,color='r')
plt.axis([0,6,0,6])
plt.show()

x_predict=6
y_predict=a*x_predict+b
print(y_predict)

3.向量化

把上面用for循环求解a和b的过程转换成向量的相乘，速度会快得多。

x_mean,y_mean=np.mean(x),np.mean(y)
a=(x-x_mean).dot(y-y_mean)/(x-x_mean).dot(x-x_mean)
b=y_mean-a*x_mean

4.衡量线性回归的的性能

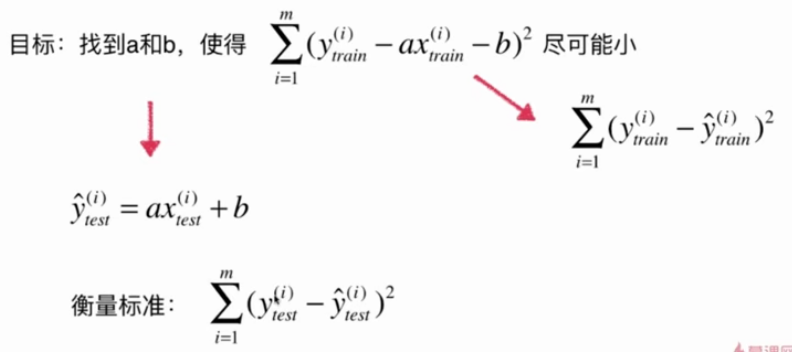
此衡量标准和m相关，通常需要除以m。

均方误差MSE：

均方根误差RMSE：（量纲和y的量纲一致）

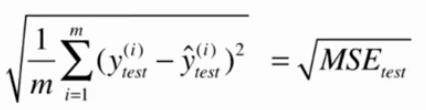
平均绝对误差MAE：

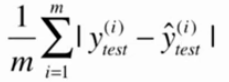
import numpy as np
import matplotlib.pyplot as plt
from sklearn import datasets

#波士顿房产数据
boston=datasets.load_boston()
print(boston.feature_names)

x=boston.data[:,5]      #只使用房间数这一特征 (506,)
y=boston.target         #(506,)

x=x[y<50.0]            #去除掉采集样本拥有的上限点
y=y[y<50.0]

from sklearn.model_selection import train_test_split   
x_train,x_test,y_train,y_test=train_test_split(x,y,random_state=666)   #x_train(392,)   x_test(98,)

#调用手动编写的简单线性回归算法（本质和上面一样）
from playML.SimpleLinearRegression import SimpleLinearRegression
reg=SimpleLinearRegression()
reg.fit(x_train,y_train)

plt.scatter(x_train,y_train)
plt.plot(x_train,reg.predict(x_train),color='r')
plt.show()

y_predict=reg.predict(x_test)

#手动计算MSE
mse_test=np.sum((y_predict-y_test)**2/len(y_test))
print(mse_test)
#调用库计算MSE
from sklearn.metrics import mean_squared_error
print(mean_squared_error(y_test, y_predict))

#计算RMSE
from math import sqrt
rmse_test=sqrt(mse_test)
print(rmse_test)

#手动计算MAE
mae_test=np.sum(np.absolute(y_predict-y_test)/len(y_test))
print(mae_test)
#调用库计算MAE
from sklearn.metrics import mean_absolute_error
print(mean_absolute_error(y_test, y_predict))

相比分类问题（可以用准确度来衡量，且0最差，1最好），回归问题针对不同的问题，评估出的数据会相差很大，所以引出R方。

R方（R Squared）

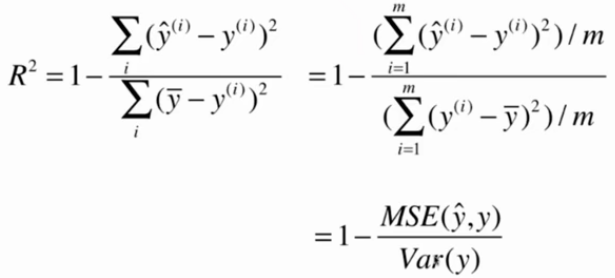
分子描述的是使用我们的模型预测产生的错误

分母描述的是使用y=y的平均值预测产生的错误（Baseline Model）

#接着上面的代码
#手动计算R方
print(1-mean_squared_error(y_test, y_predict)/np.var(y_test))
#调用库计算R方
from sklearn.metrics import r2_score
print(r2_score(y_test, y_predict))

5.多元线性回归

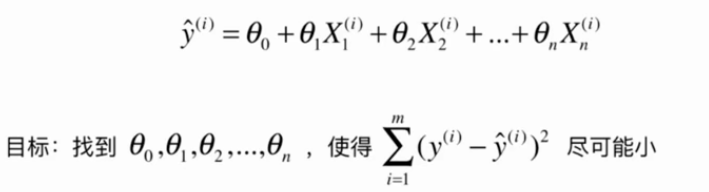
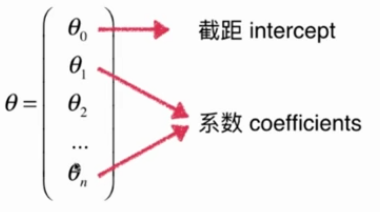
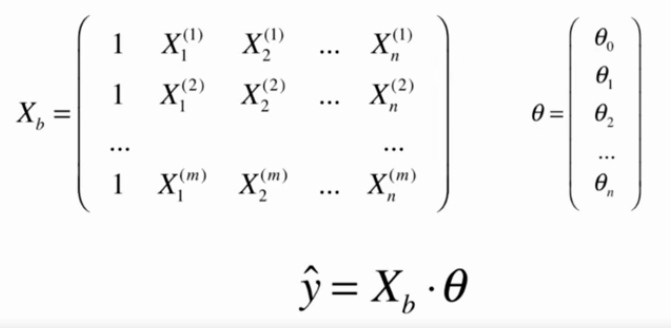
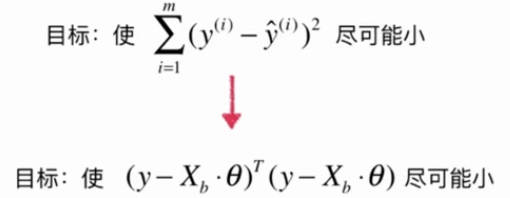
多元线性回归的正规方程解：

6.使用scikit-learn解决回归问题

import numpy as np
from sklearn import datasets

#波士顿房产数据
boston=datasets.load_boston()

X=boston.data    
y=boston.target         

X=X[y<50.0]            #去除掉采集样本拥有的上限点
y=y[y<50.0]

from sklearn.model_selection import train_test_split   
X_train,X_test,y_train,y_test=train_test_split(X,y,random_state=666)   

from sklearn.linear_model import LinearRegression
lin_reg=LinearRegression()
lin_reg.fit(X_train,y_train)
print(lin_reg.coef_)         #系数
print(lin_reg.intercept_)    #截距
print(lin_reg.score(X_test, y_test))

7.使用KNN解决回归问题

import numpy as np
from sklearn import datasets

#波士顿房产数据
boston=datasets.load_boston()

X=boston.data    
y=boston.target         

X=X[y<50.0]            #去除掉采集样本拥有的上限点
y=y[y<50.0]

from sklearn.model_selection import train_test_split   
X_train,X_test,y_train,y_test=train_test_split(X,y,random_state=666)   

from sklearn.neighbors import KNeighborsRegressor
knn_reg=KNeighborsRegressor()
knn_reg.fit(X_train,y_train)
print(knn_reg.score(X_test,y_test))

from sklearn.model_selection import GridSearchCV
param_grid=[
    {
          'weights':['uniform'],
          'n_neighbors':[i for i in range(1,11)]
      },
    {
          'weights':['distance'],
          'n_neighbors':[i for i in range(1,11)],
          'p':[i for i in range(1,6)]
      }
    ]
knn_reg=KNeighborsRegressor()
grid_search=GridSearchCV(knn_reg, param_grid,n_jobs=-1,verbose=1)
grid_search.fit(X_train,y_train)

print(grid_search.best_params_)       #查看最好的参数
print(grid_search.best_score_)        #使用CV标准下的得分
print(grid_search.best_estimator_.score(X_test,y_test))