#198 House Robber
You are a professional robber planning to rob houses along a street. Each house has a certain amount of money stashed, the only constraint stopping you from robbing each of them is that adjacent houses have security system connected and it will automatically contact the police if two adjacent houses were broken into on the same night.
Given a list of non-negative integers representing the amount of money of each house, determine the maximum amount of money you can rob tonight without alerting the police.
去掉故事背景就是说,一个含有n个元素的数组(元素值当然大于0),从中取出m个位置的元素,要求相邻两个位置的元素最多仅仅能取一个。求能获得元素值和的最大值
典型的DP问题。
自顶向下分析问题。n个元素的数组取和的最大值 f(n) ,能够转换为
max{ f(n-1) , f(n-2)+nums[n] }
利用数组a[n]保存中间子问题结果,算法例如以下:
注:依据故事背景。一条街上的住户不超过1000家吧。。。
//0ms
int rob(int* nums, int numsSize) {
int i=0,t1,t2;
int a[1000]={0};
if(numsSize==1)
{
a[0] = nums[0];
return a[0];
}
if(numsSize==2)
{
a[1] = (nums[0]>=nums[1]) ? nums[0]:nums[1];
return a[1];
}
if(numsSize==3)
{
if(nums[0]+nums[2]>=nums[1])
a[3] = nums[0]+nums[2];
else
a[3] = nums[1];
return a[3];
}
if(numsSize>3)
{
a[0] = nums[0];
a[1] = (nums[0]>=nums[1]) ? nums[0]:nums[1];
if(nums[0]+nums[2]>=nums[1])
a[2] = nums[0]+nums[2];
else
a[2] = nums[1];
for(i=3;i<numsSize;i++)
{
//t1 = rob(nums,numsSize-1);
//t2 = rob(nums,numsSize-2)+nums[numsSize-1];
t1 = a[i-1];
t2 = a[i-2]+nums[i];
a[i] = (t1>=t2)?
t1:t2;
}
}
return a[numsSize-1];
}
# 202 Happy Number
Write an algorithm to determine if a number is "happy".
A happy number is a number defined by the following process: Starting with any positive integer, replace the number by the sum of the squares of its digits, and repeat the process until the number equals 1 (where it will stay), or it loops endlessly in a cycle which does not include 1. Those numbers for which this process ends in 1 are happy numbers.
Example: 19 is a happy number
- 12 + 92 = 82
- 82 + 22 = 68
- 62 + 82 = 100
- 12 + 02 + 02 = 1
仅仅要出现循环就不是Happy Number
对于int型(10位)每一位平方和 小于: 9^2 * 10 = 810 ;能够用一个数组保存和 ,当再次出现该值时说明出现了一个循环,返回false
//0ms
bool isHappy(int n) {
int hash[810]={0};
int i=1,new_n=0;
if(n==1)
return true;
while(n!=1)
{
new_n = 0;
while(n)
{
new_n += (n%10)*(n%10);
n = n/10;
}
n = new_n;
if(n==1)
return true;
if(hash[n]==1)
return false;
else
hash[n] = 1;
}
}基于事实1 是 Happy Number 而 2,3,4,5,6均不是Happy Number 为了使空间复杂度变为为O(1),可採用例如以下算法
//0ms
bool isHappy(int n)
{
int next;
while(n > 6)
{
next = 0;
while(n)
{
next += (n%10) * (n%10);
n /= 10;
}
n = next;
}
return n == 1;
}#203 Remove Linked List Elements
Remove all elements from a linked list of integers that have value val.
Example
Given: 1 --> 2 --> 6 --> 3 --> 4 --> 5 --> 6, val = 6
Return: 1 --> 2 --> 3 --> 4 --> 5
<span style="font-size:10px;">//12ms
/**
* Definition for singly-linked list.
* struct ListNode {
* int val;
* struct ListNode *next;
* };
*/
struct ListNode* removeElements(struct ListNode* head, int val) {
struct ListNode *newhead,*p,*q;
if(!head)
return NULL;
newhead->next = head; //简化代码,加入头结点 q p
q = newhead;
p = head;
while(p)
{
if(p->val==val)
q->next = p->next;//q 不变 p后移
else
q = p;// q p 都后移
p = p->next;
}
return newhead->next;
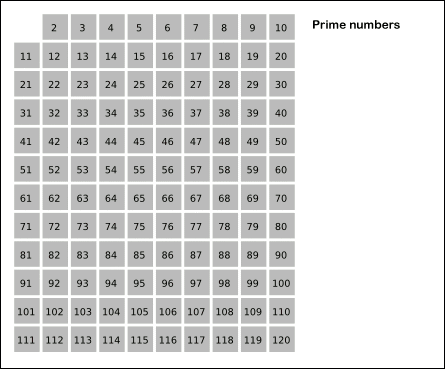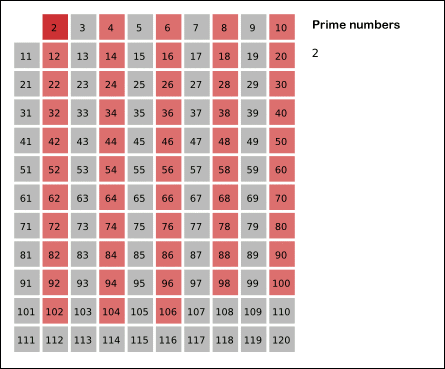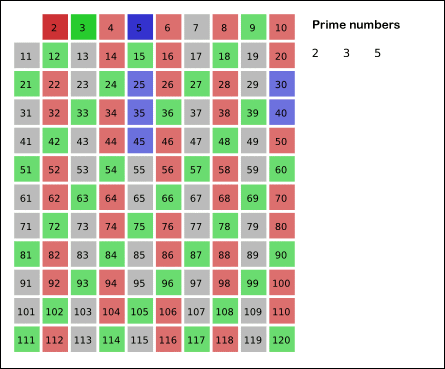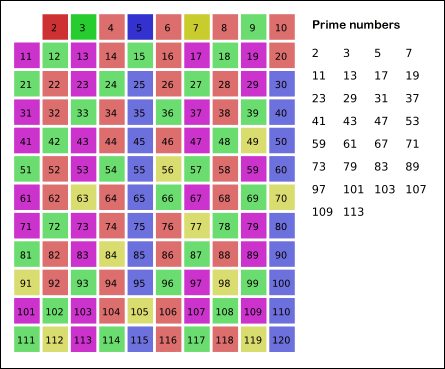
}</span>#204 Count Primes
Count
the number of prime numbers less than a non-negative number, n.
求1~n-1之间素数的个数,注意1不是素数
推断 n 是一个素数的方法是,不能被 2 ~ sqrt(n) 之间的数整除。即约数仅仅有1和其本身
在Leetcode Discuss中看到例如以下解法:时间和空间复杂度都接近O(n)
https://leetcode.com/discuss/34622/my-c-solutions-in-44ms-time-nearly-o-n-and-space-nearly-o-n
//44ms
/*1. trick1 is to use square root of n.
2. trick2 is not to use non-prime numbers as the step
3. trick3 is to use i*i as the start.
4. trick4 is to use count-- in every loop, avoiding another traversal. */
int countPrimes(int n) {
if(n <= 2) return 0;
if(n == 3) return 1;
bool *prime= (bool*)malloc(sizeof(bool)*n);
int i=0,j=0;
int count = n-2;
int rt = sqrt(n);//trick1
for(j = 0; j < n; j++)
{
prime[j] = 1;
}
for(i = 2; i <= rt; i++)
{
if (prime[i])//trick2
{
for(j=i*i ; j<n ; j+=i)//trick3
{
if (prime[j])
{
prime[j]=0;
count--;//trick4
}
}
}
}
free(prime);
return count;
}