引入
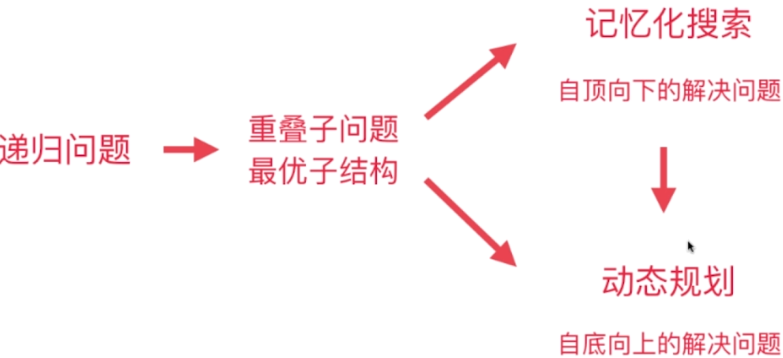
- 以求解斐波那契数列为例,如何避免递归中的重复计算
- 记忆化搜索(指数->线性,对于n=40,性能提升100万倍)

1 #include <iostream> 2 #include <ctime> 3 #include <vector> 4 using namespace std; 5 6 vector<int> memo; 7 8 int num = 0 ; 9 10 int fib(int n){ 11 12 num ++; 13 14 if( n == 0 ) 15 return 0; 16 17 if( n == 1 ) 18 return 1; 19 20 if( memo[n] == -1 ) 21 memo[n] = fib(n-1) + fib(n-2); 22 23 return memo[n]; 24 } 25 26 int main(){ 27 28 num = 0 ; 29 30 int n = 40; 31 memo = vector<int>(n+1,-1); 32 33 time_t startTime = clock(); 34 int res = fib(n); 35 time_t endTime = clock(); 36 37 cout << "fib("<<n<<") = "<<res<<endl; 38 cout << "time:"<<double(endTime-startTime)/CLOCKS_PER_SEC<<" s"<<endl; 39 cout << "run function fib() "<<num<<" times."<< endl; 40 41 return 0; 42 }
-
- 自下而上(动态规划)
- 将原问题拆解成若干子问题,同时保存子问题的答案,使得每个子问题只求解一次,最终获得原问题的答案
- 自下而上(动态规划)

1 int fib2(int n){ 2 vector<int> memo(n+1, -1); 3 memo[0] = 0; 4 memo[1] = 1; 5 for(int i = 2 ; i <= n ; i ++ ){ 6 memo[i] = memo[i-1] + memo[i-2]; 7 } 8 return memo[n]; 9 }