Description
A common pastime for poker players at a poker table is to shuffle stacks of chips. Shuffling chips is performed by starting with two stacks of poker chips, S1 and S2, each stack containing C chips. Each stack may contain chips of several different colors.
The actual shuffle operation is performed by interleaving a chip from S1 with a chip from S2 as shown below for C = 5:
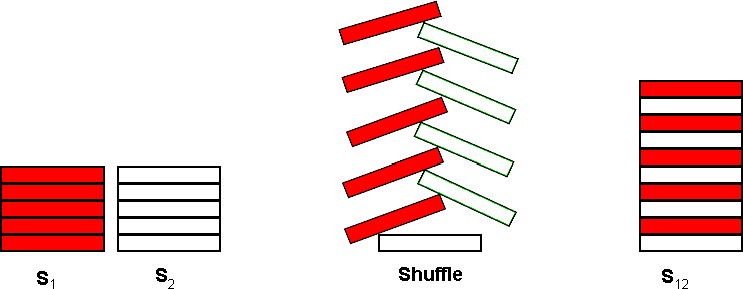
The single resultant stack, S12, contains 2 * C chips. The bottommost chip of S12 is the bottommost chip from S2. On top of that chip, is the bottommost chip from S1. The interleaving process continues taking the 2nd chip from the bottom of S2 and placing that on S12, followed by the 2nd chip from the bottom of S1 and so on until the topmost chip from S1 is placed on top of S12.
After the shuffle operation, S12 is split into 2 new stacks by taking the bottommost C chips from S12 to form a new S1 and the topmost C chips from S12 to form a new S2. The shuffle operation may then be repeated to form a new S12.
For this problem, you will write a program to determine if a particular resultant stack S12 can be formed by shuffling two stacks some number of times.
Input
The first line of input contains a single integer N, (1 ≤ N ≤ 1000) which is the number of datasets that follow.
Each dataset consists of four lines of input. The first line of a dataset specifies an integer C, (1 ≤ C ≤ 100) which is the number of chips in each initial stack (S1 and S2). The second line of each dataset specifies the colors of each of the C chips in stack S1, starting with the bottommost chip. The third line of each dataset specifies the colors of each of the C chips in stack S2 starting with the bottommost chip. Colors are expressed as a single uppercase letter (A through H). There are no blanks or separators between the chip colors. The fourth line of each dataset contains 2 * C uppercase letters (A through H), representing the colors of the desired result of the shuffling of S1 and S2 zero or more times. The bottommost chip’s color is specified first.
Output
Output for each dataset consists of a single line that displays the dataset number (1 though N), a space, and an integer value which is the minimum number of shuffle operations required to get the desired resultant stack. If the desired result can not be reached using the input for the dataset, display the value negative 1 (−1) for the number of shuffle operations.
Sample Input
2 4 AHAH HAHA HHAAAAHH 3 CDE CDE EEDDCC
Sample Output
1 2 2 -1
大致题意:输入一个N,表示有N组数据,每组数据有四行,第一行是一个整数C,表示 每堆牌的数量,接下来是三行字符序列,第一行是S1堆,第二行是S2堆,第三行S12是预想的排序序列,求需要几步才能到达预想序列。
已知两堆牌s1和s2的初始状态, 其牌数均为c,按给定规则能将他们相互交叉组合成一堆牌s12,再将s12的最底下的c块牌归为s1,最顶的c块牌归为s2,依此循环下去。现在输入s1和s2的初始状态 以及 预想的最终状态s12.问s1 s2经过多少次洗牌之后,最终能达到状态s12,若永远不可能相同,则输出"-1"。
思路就是过程模拟,感觉最机智的就是用map<string,bool>vis,来标记字符序列了。

1 #include <iostream> 2 #include <cstring> 3 #include <map> 4 using namespace std; 5 const int maxn=110; 6 char s1[maxn],s2[maxn]; 7 char s12[maxn<<1]; //预想的牌的状态 8 int main() 9 { 10 int n,c,cnt=0; 11 cin>>n; 12 while(n--) 13 { 14 cin>>c; 15 cin>>s1>>s2>>s12; 16 int step=0; 17 map<string,bool>vis; 18 vis[s12]=true; 19 while(1) 20 { 21 char temp[maxn<<1]; 22 int k=0; 23 for(int i=0;i<c;i++) //把s1和s2按照错乱顺序放到临时变量中 24 { 25 temp[k++]=s2[i]; 26 temp[k++]=s1[i]; 27 } 28 temp[k++]='�'; 29 step++; 30 if(strcmp(temp,s12)==0) //如果和预设匹配,就输出步数 31 { 32 cout<<++cnt<<' '<<step<<endl; 33 break; 34 } 35 else if(vis[temp]&&strcmp(temp,s12)!=0) //如果成环了,表示无法匹配了,输出-1 36 { 37 cout<<++cnt<<' '<<-1<<endl; 38 break; 39 } 40 vis[temp]=true; //标记这个序列出现过 41 strncpy(s1,temp,c); //把temp数组的钱c个字符放进s1 42 strncpy(s2,temp+c,c); //把temp数组下面c个字符放进s2 43 s1[c]=s2[c]='�'; 44 // cout<<"--"<<s1<<"--"<<s2<<endl; 45 } 46 } 47 return 0; 48 }
