1/12
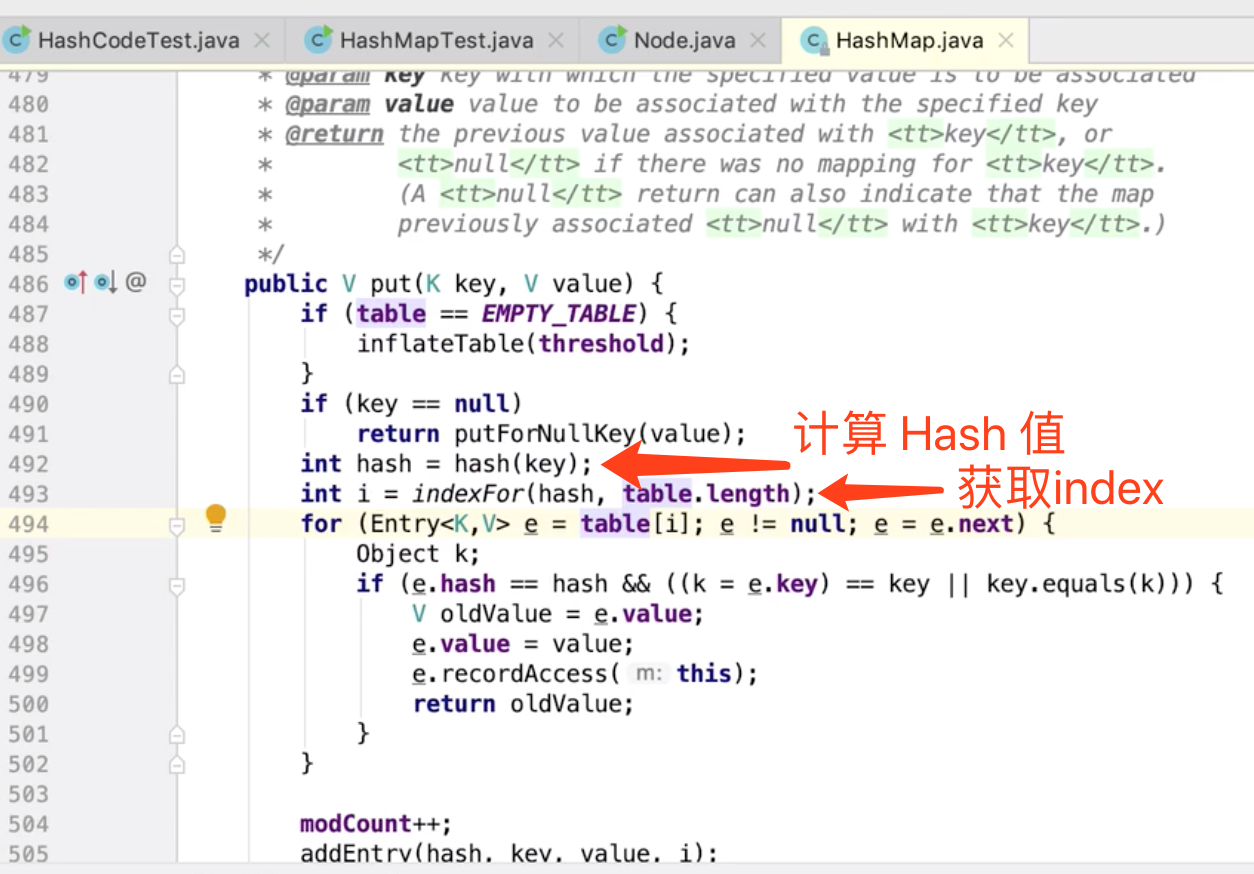
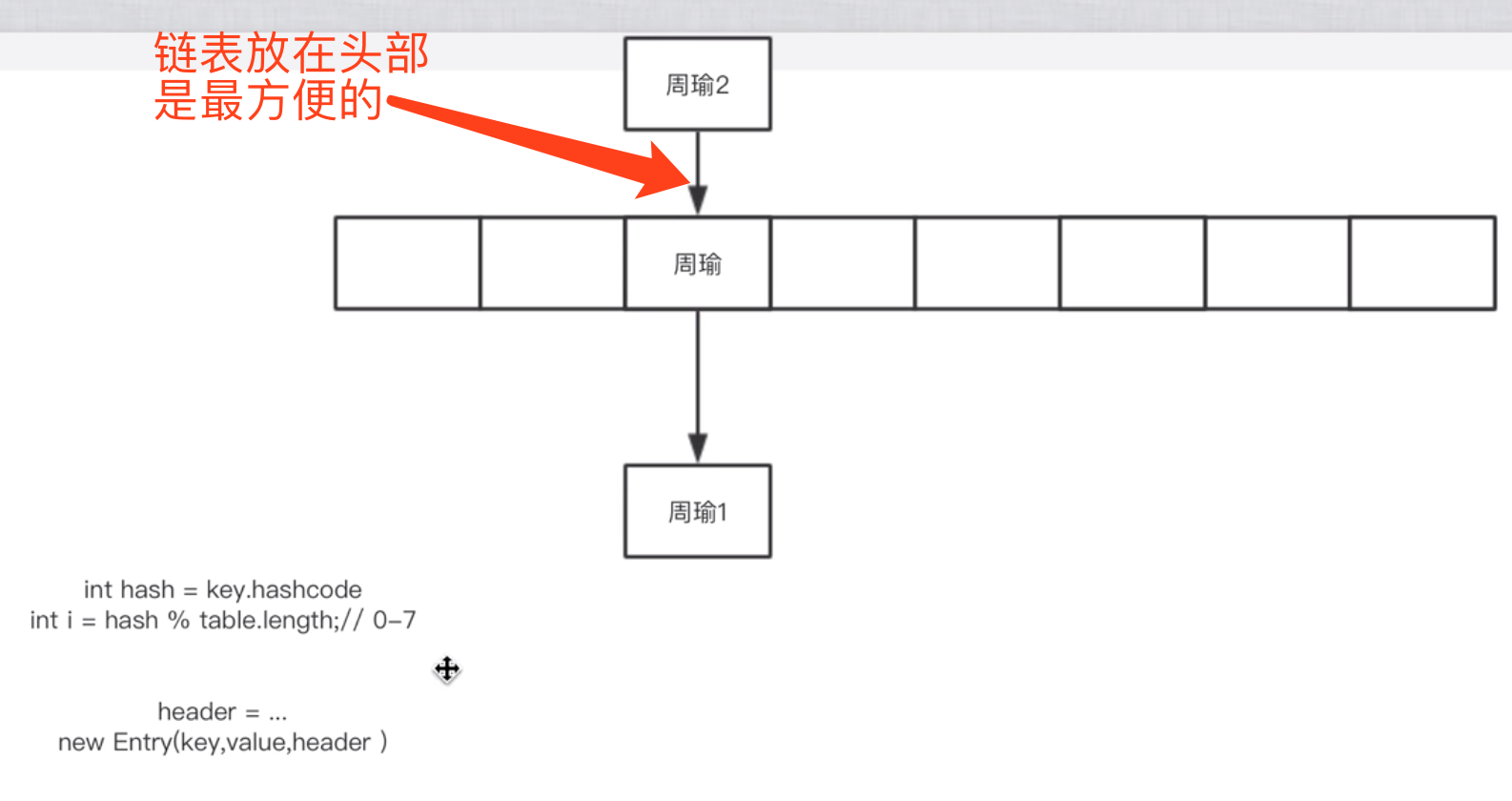
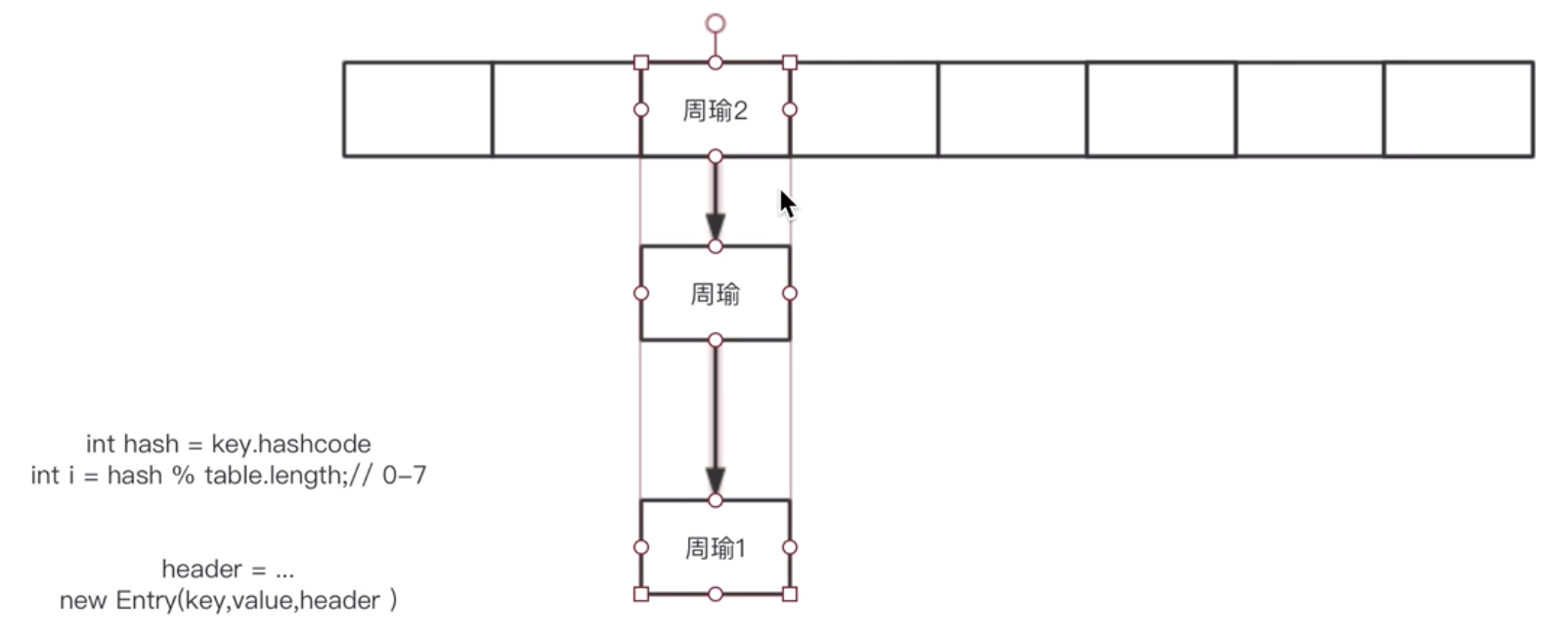
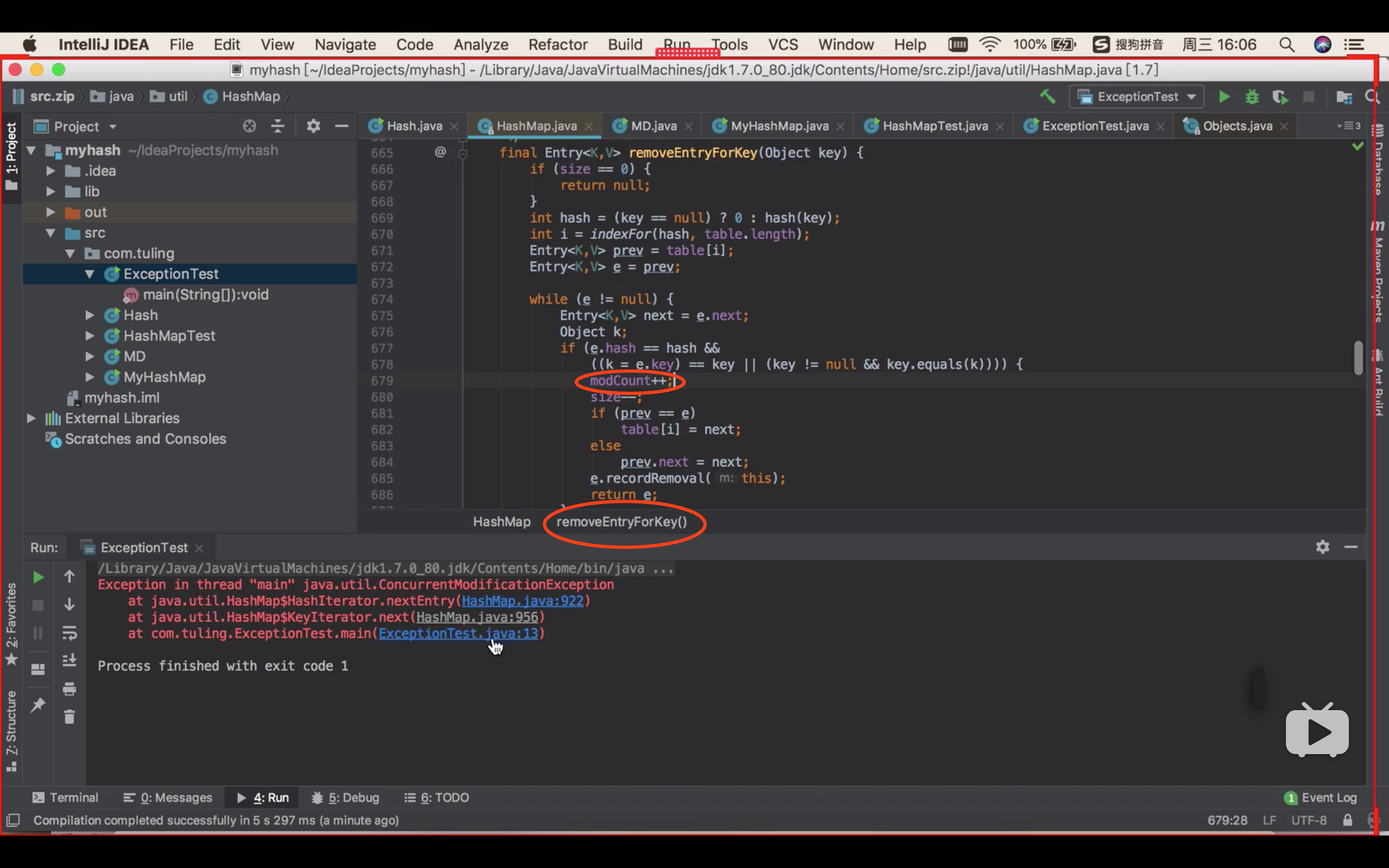
插入链表头部以后,向下移动一下。。。
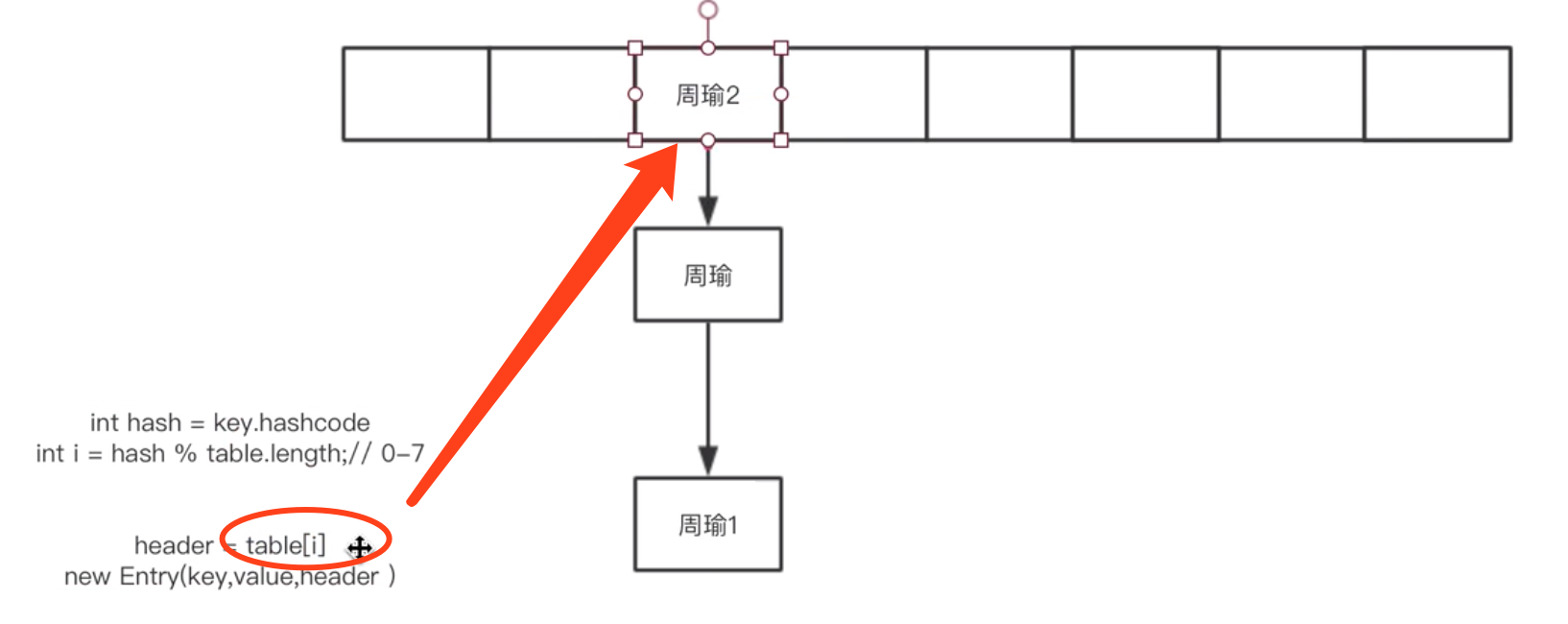


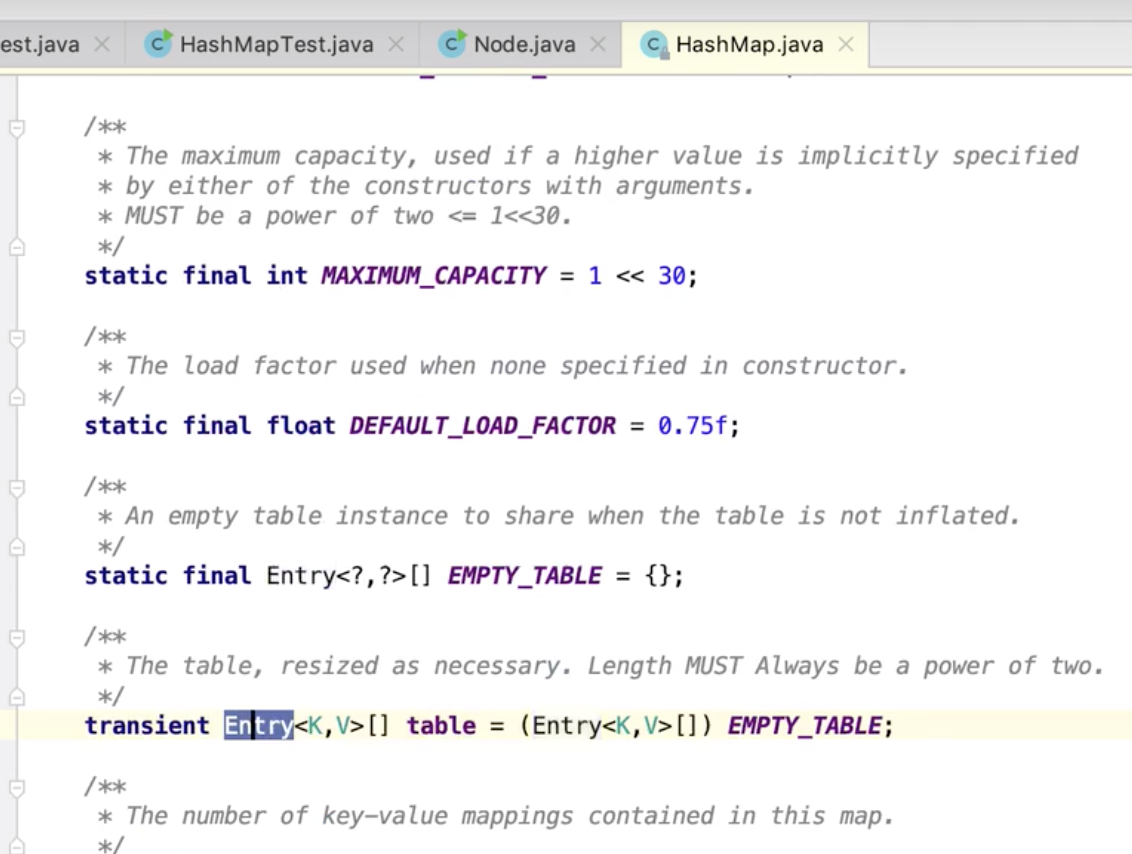
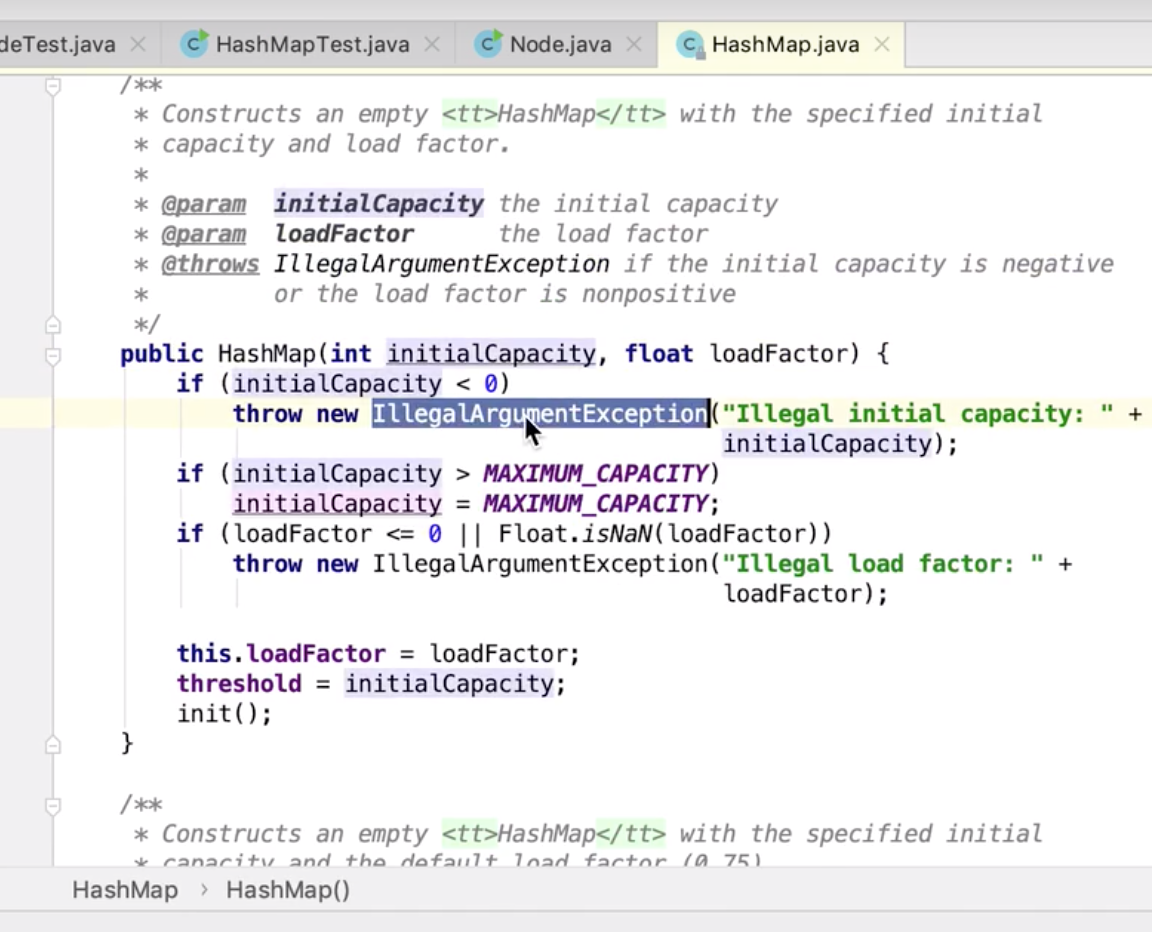



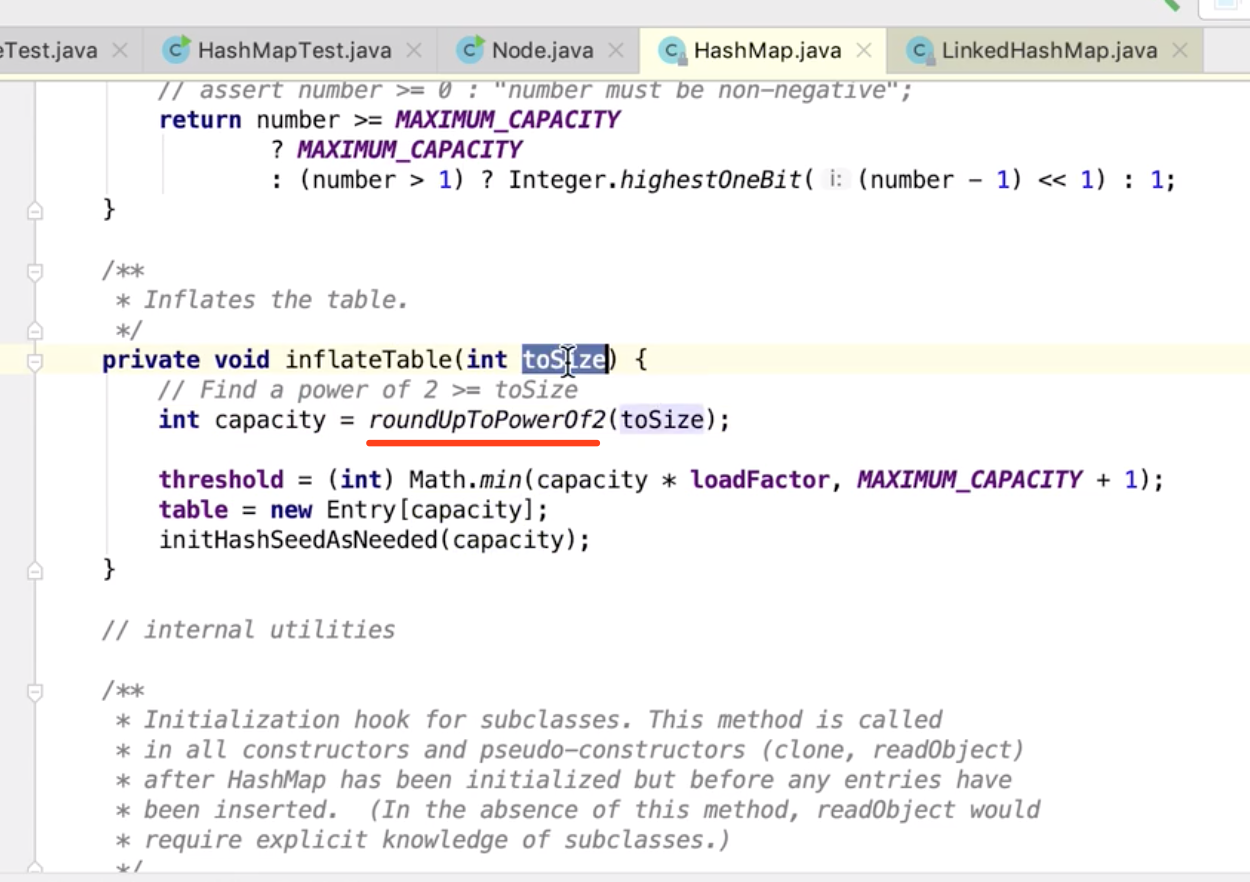




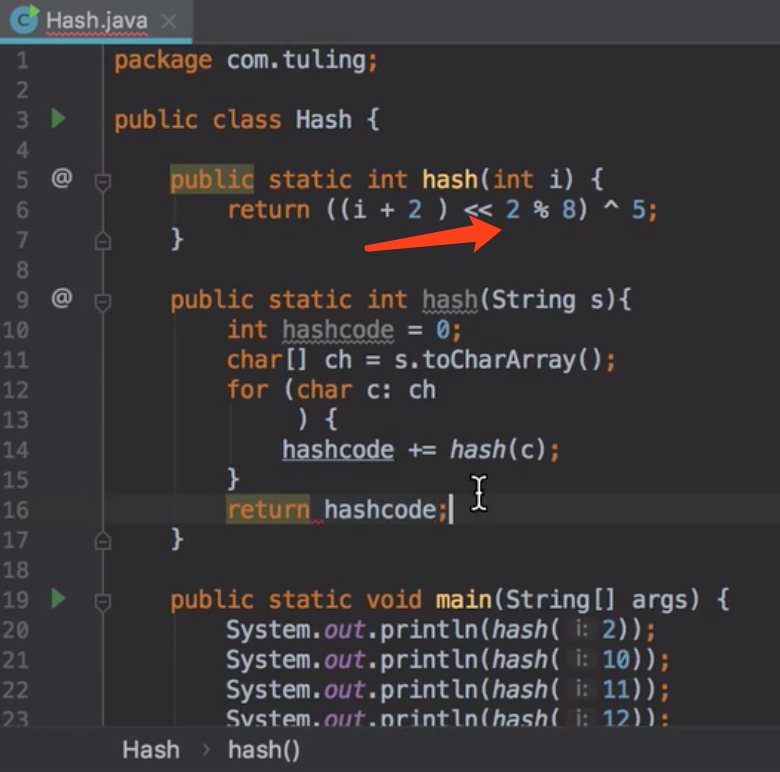
Integer.highestOneBit(int i)方法的作用与底层实现在Integer类中有这么一个方法,你可以给它传入一个数字,它将返回小于等于这个数字的一个2的幂次方数。这个方法就是highestOneBit(int i)。 比如下面的Demo,注意方法的输入与返回值: 这个方法的实现代码量也是非常少的: 接下来,我们就来详细分析一下这块代码的逻辑。 首先,对于这个方法的功能:给定一个数字,找到小于或等于这个数字的一个2的幂次方数。 如果我们要自己来实现的话,我们需要知道:怎么判断一个数字是2的幂次方数。 说真的,我一下想不到什么好方法来判断,唯一能想到的就是一个数字如果把它转换成二进制表示的话,它会有一个规律:如果一个数字是2的幂次方数,那么它对应的二进制表示仅有一个bit位上是1,其他bit位全为0。 比如: 十进制6,二进制表示为:0000 0110 十进制8,二进制表示为:0000 1000 十进制9,二进制表示为:0000 1001 所以,我们可以利用一个数字的二进制表示来判断这个数字是不是2的幂次方数。关键代码怎么实现呢?去遍历每个bit位?可以,但是不好,那怎么办?我们还是回头仔细看看Integer是如何实现的吧? 我们发现这段代码中没有任何的遍历,只有位运算与一个减法,也就是说它的实现思路和我们自己的实现思路完全不一样,它的思路就是:给定一个数字,通过一系列的运算,得到一个小于或等于该数字的一个2的幂次方数。 也就是:如果给定一个数字18,通过运算后,要得到16。 18用二进制表示为: 0001 0010 想要得到的结果(16)是:0001 0000 那么这个运算的过程无非就是将18对应的二进制数中除最高位的1之外的其他bit位都清零,则拿到了我们想要的结果。 那怎么通过位运算来实现这个过程呢? 我们拿18对应的二进制数 再将 再将 再将 再将 再将
最后用 其实这个过程可以抽象成这样: 现在有一个二进制数据, 先将 再将 再将 后面不用再推算了,到这里我们其实可以发现一个规律: 右移与或运算的目的就是想让某个数字的低位都变为1,再用该结果 减去 该结果右移一位后的结果,则相当于清零了原数字的低位。即得到了我们想要的结果。 到此,只能感叹JDK作者对于位运算的使用已经达到了出神入化的境界了。 |
|


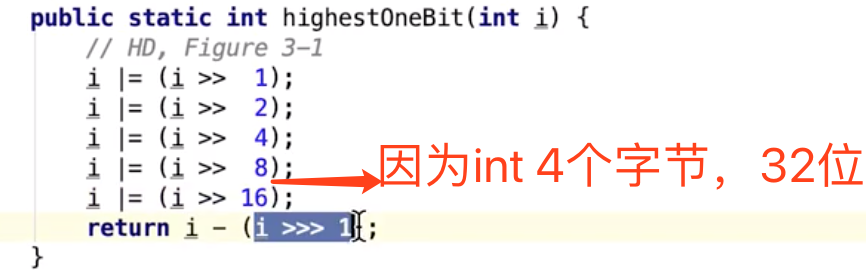
要得到 1 0...0 C
先搞成 1 1...1 A,再(无符号)右移一位 B, A-B 即得 C



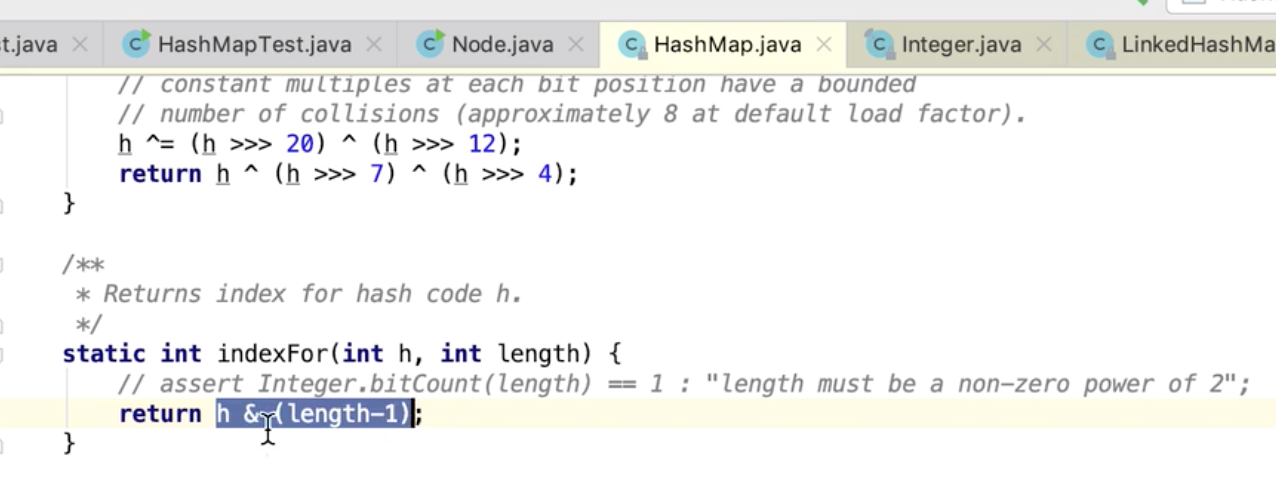



不管高位怎么变,key 计算出来都是一样

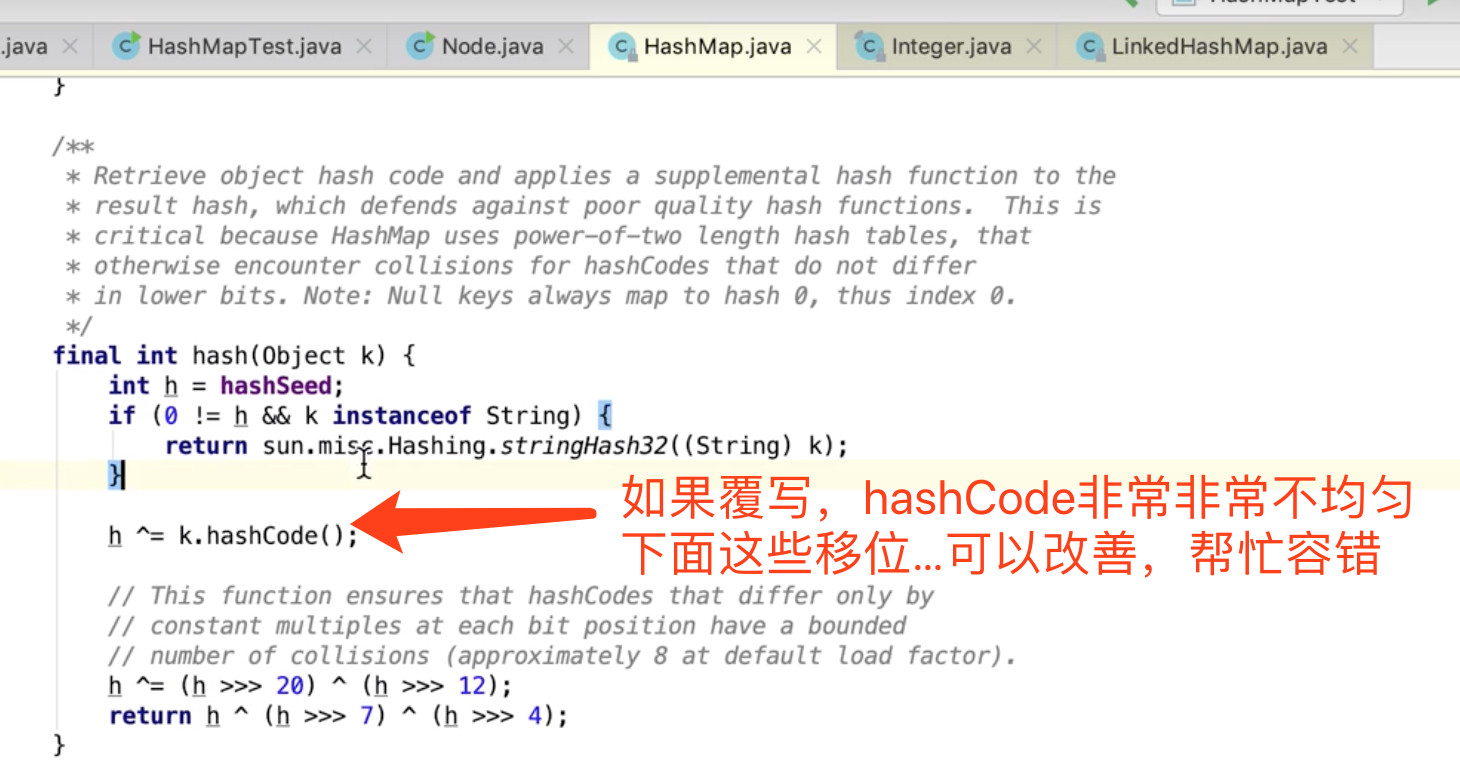
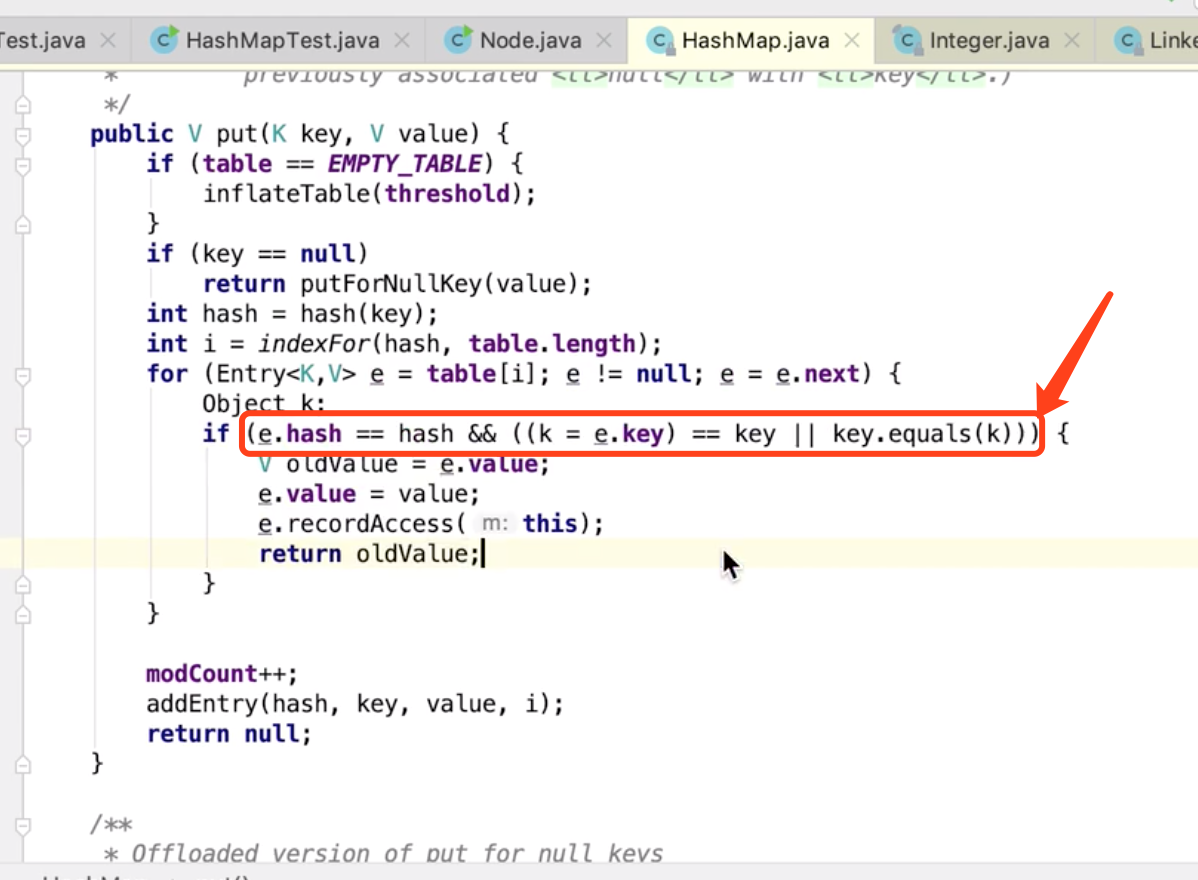
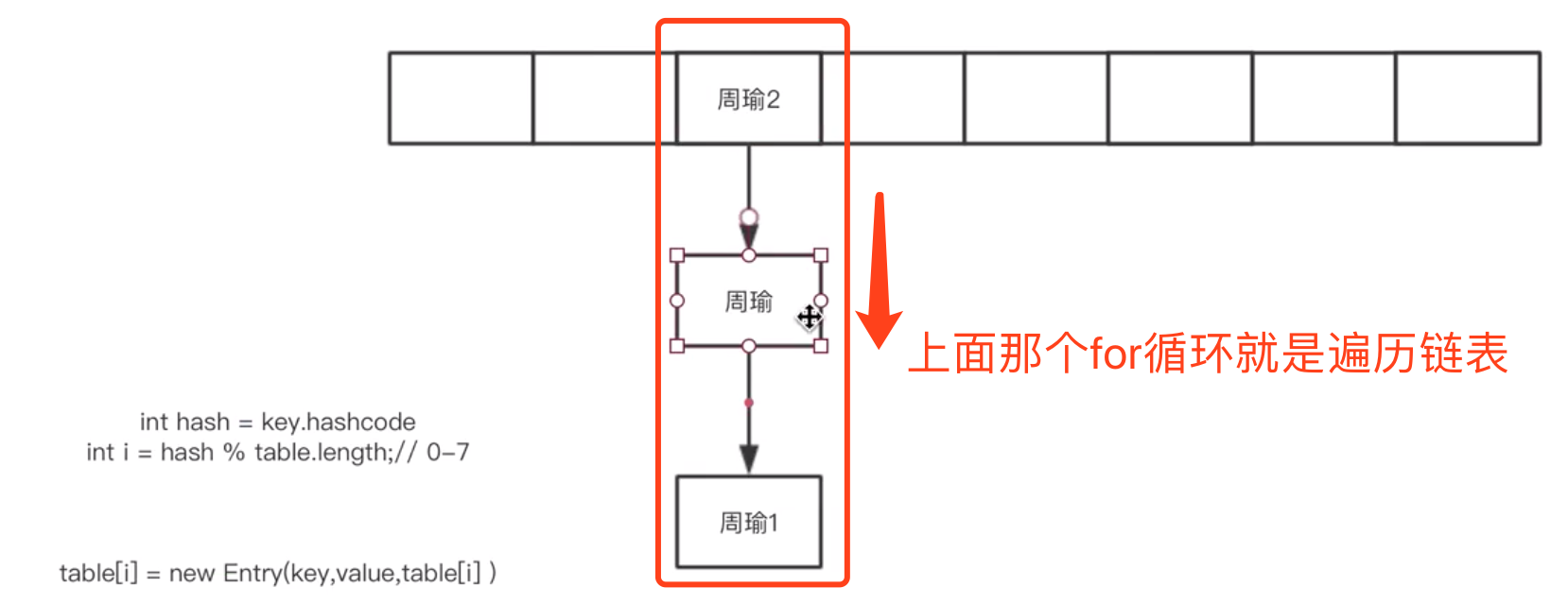

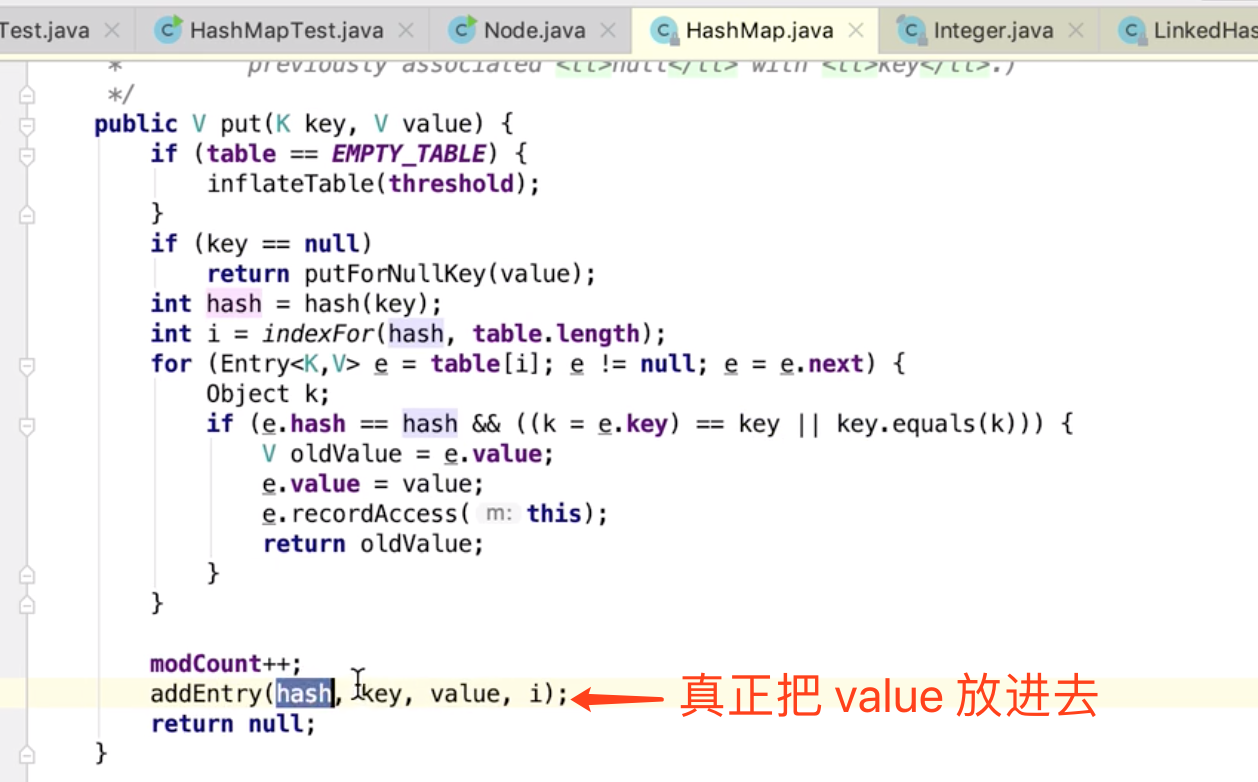
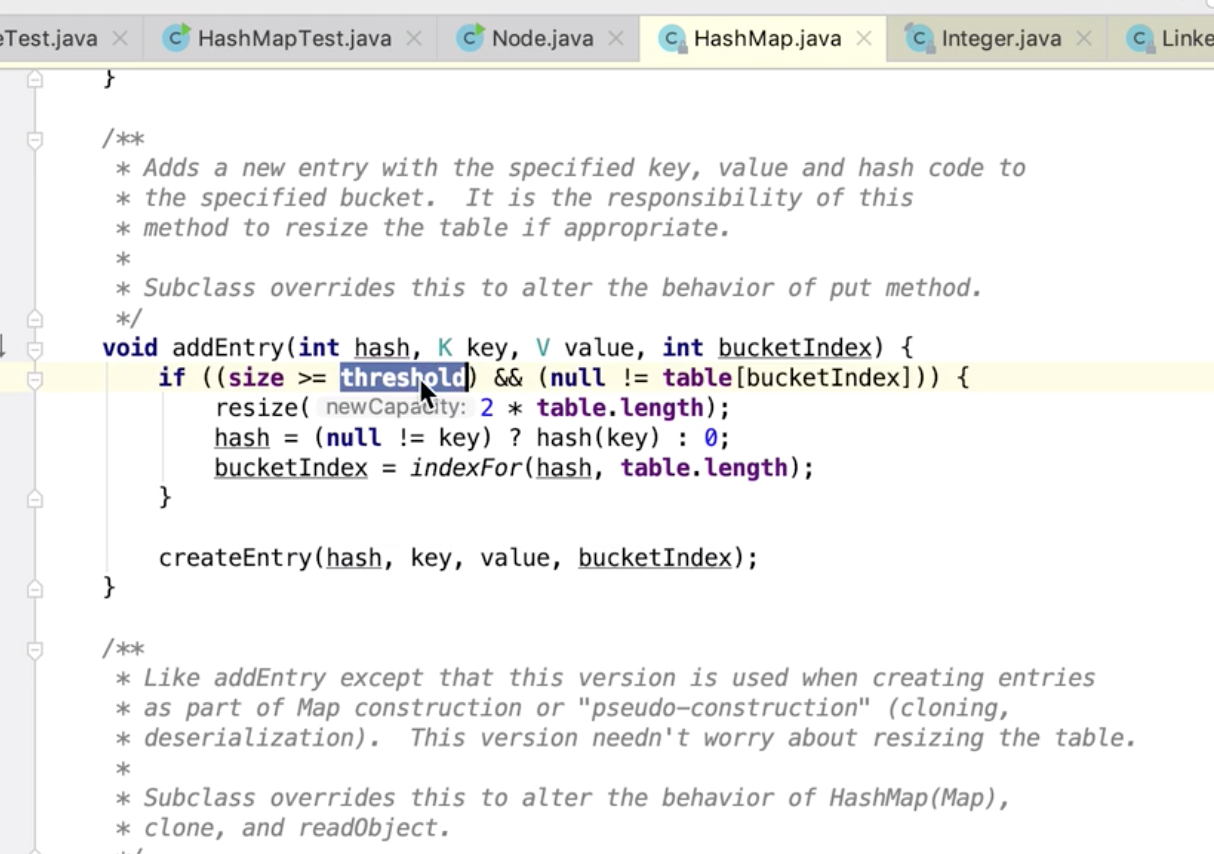
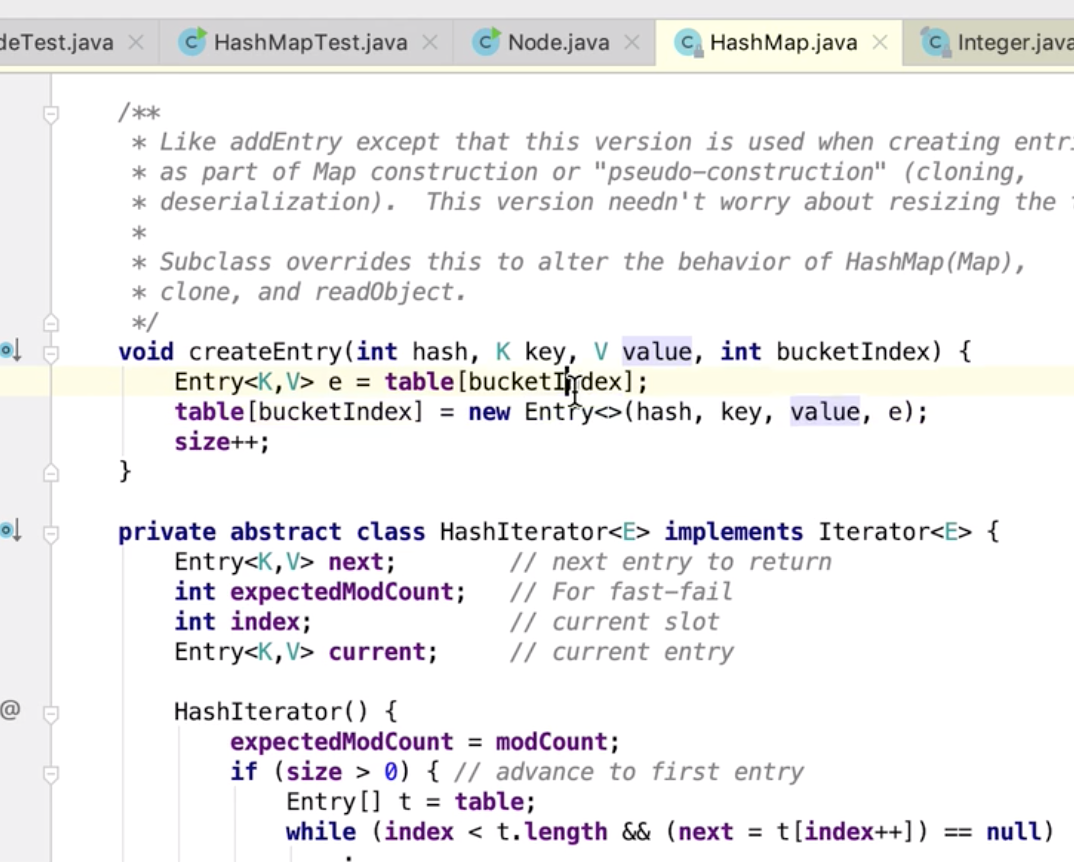



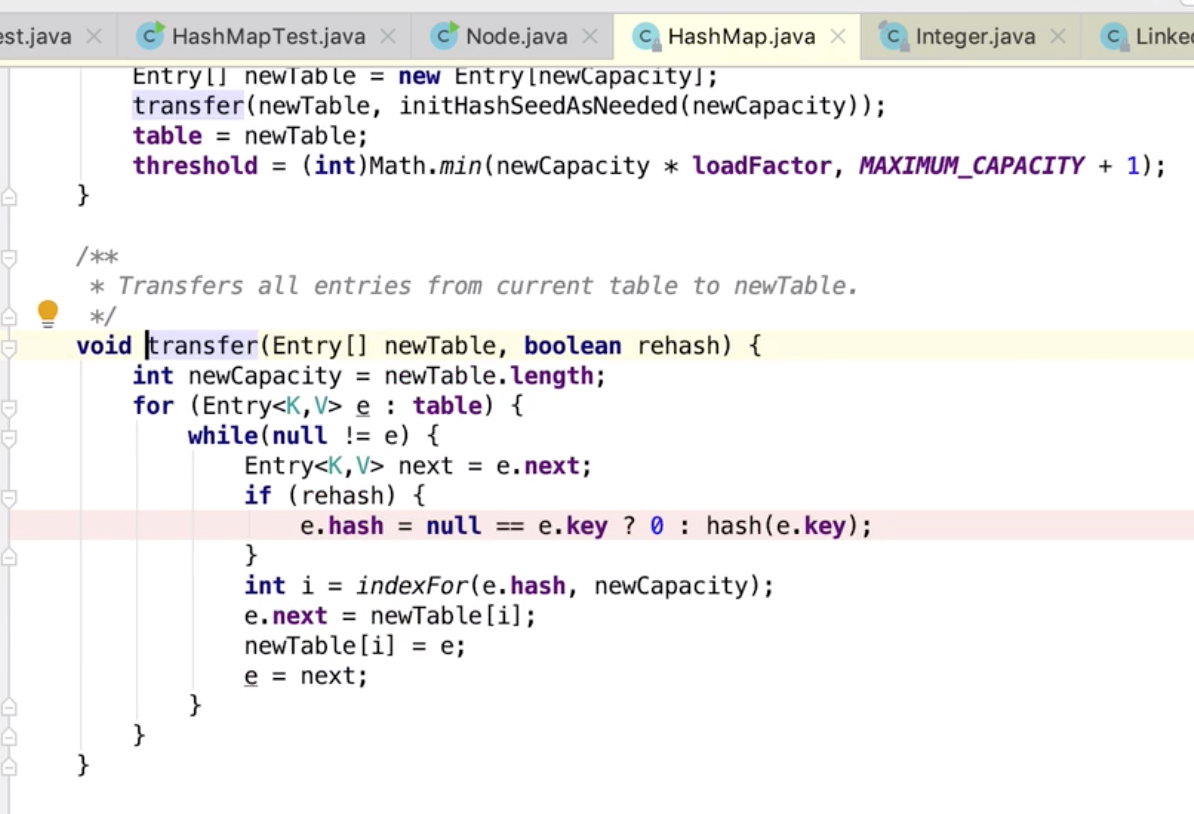

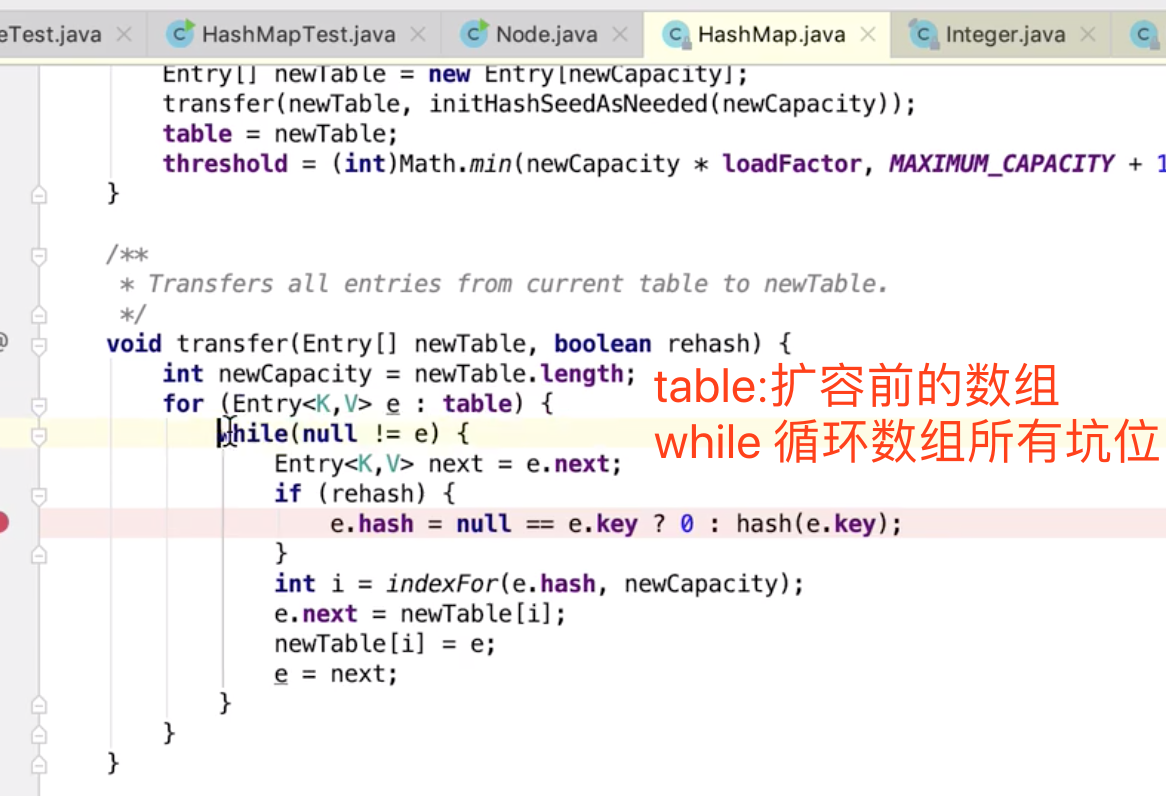

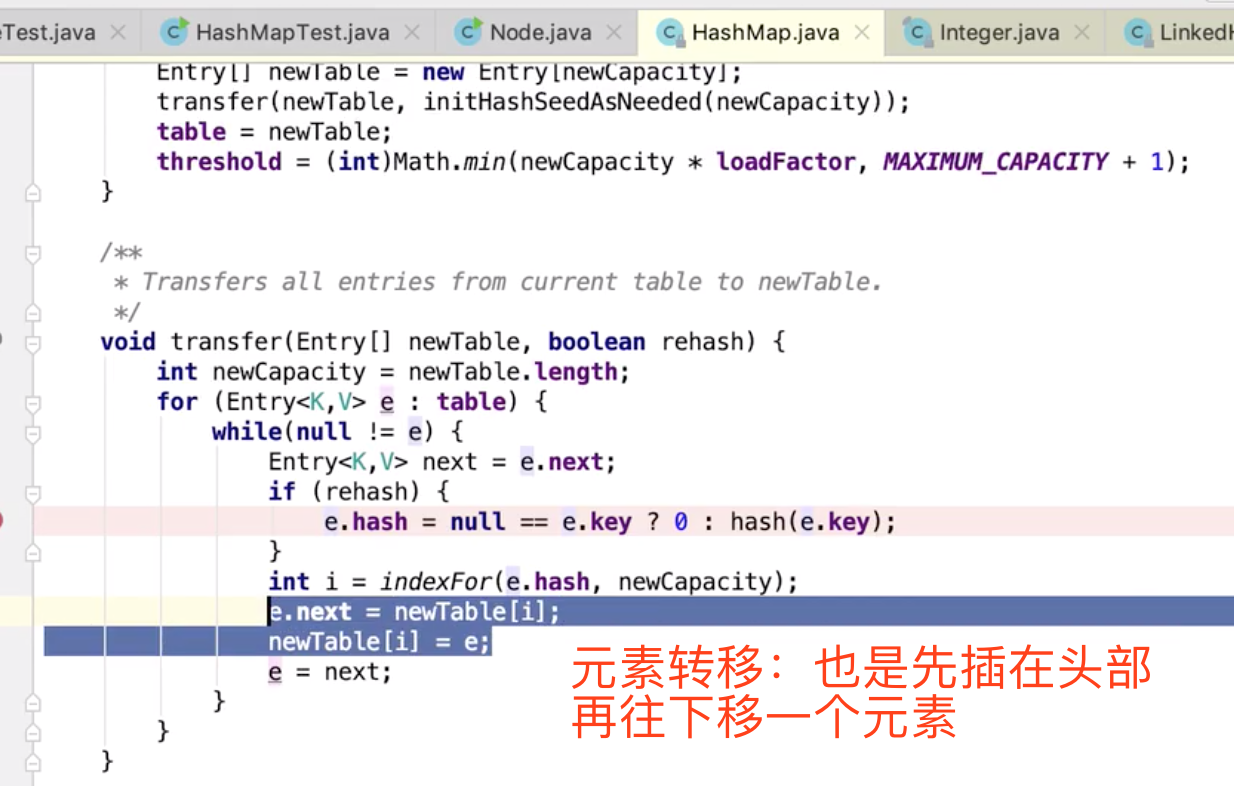
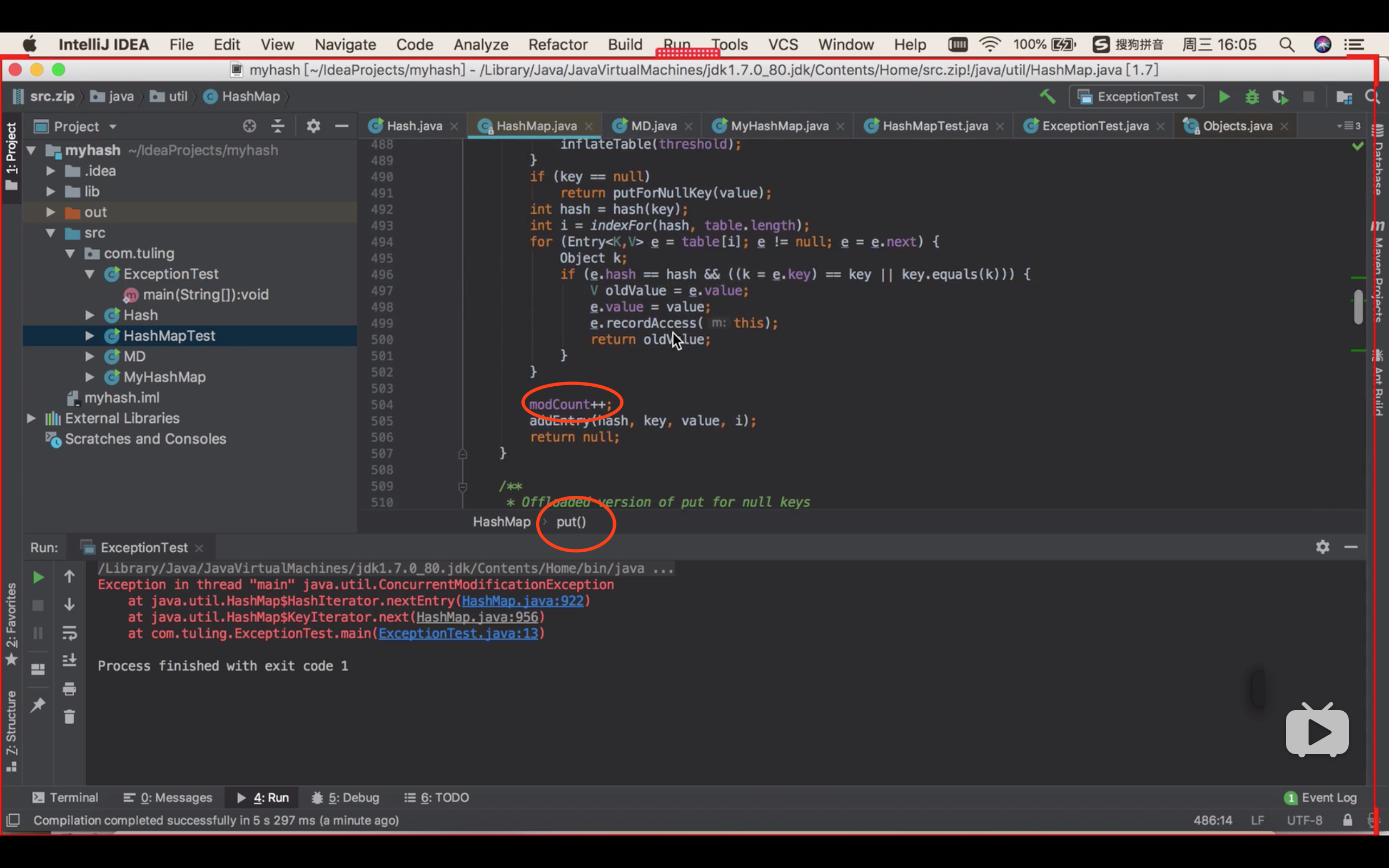
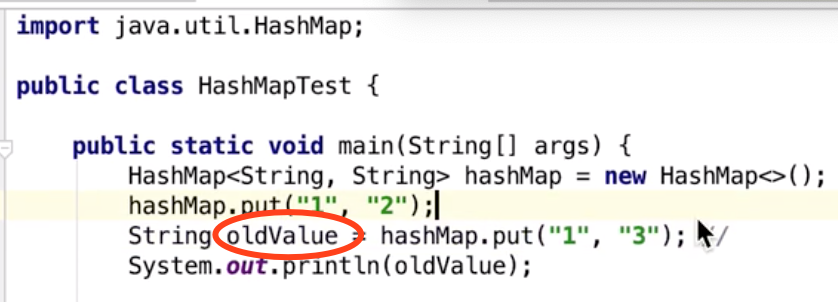
相当于一次重新put
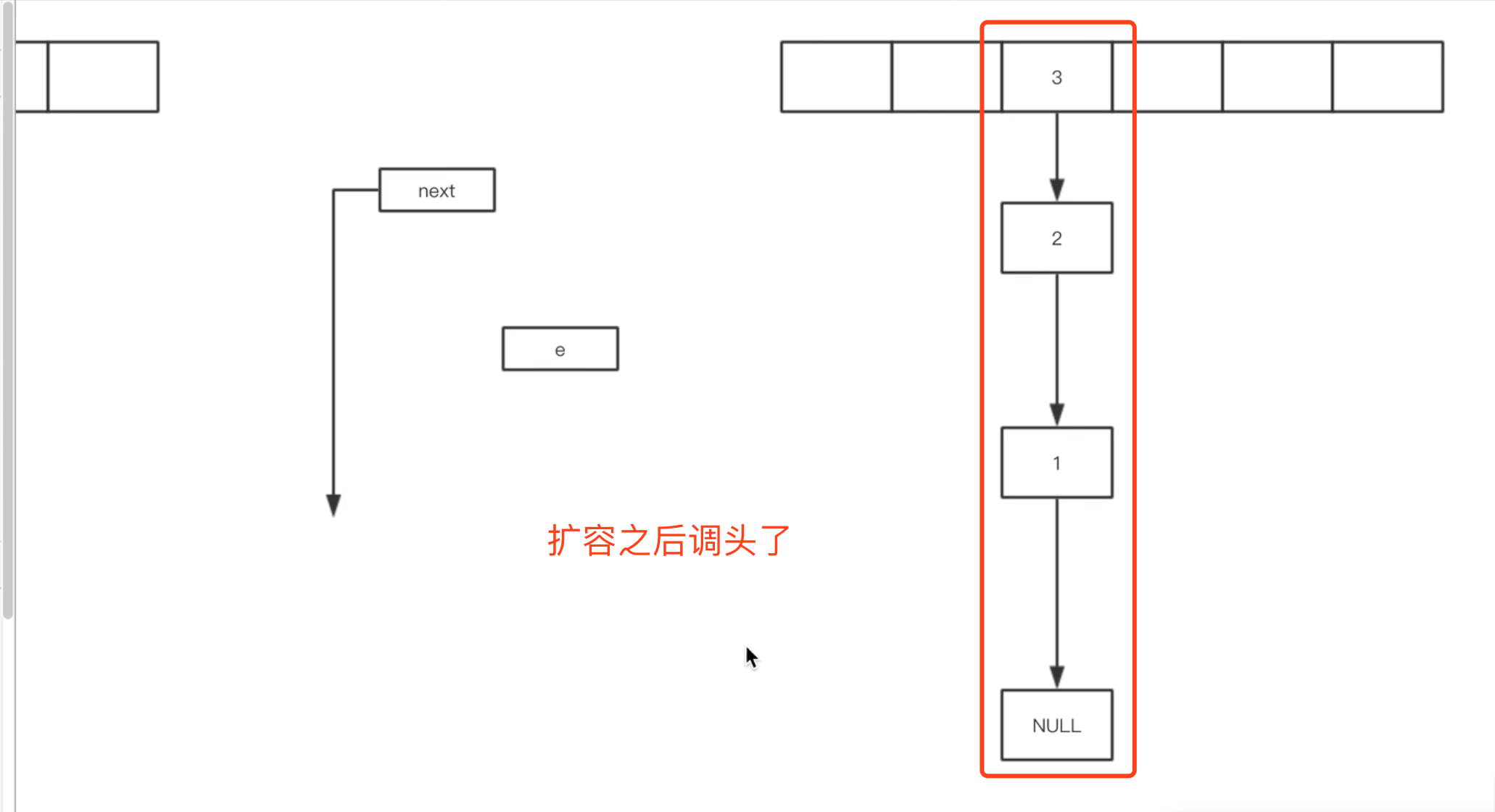
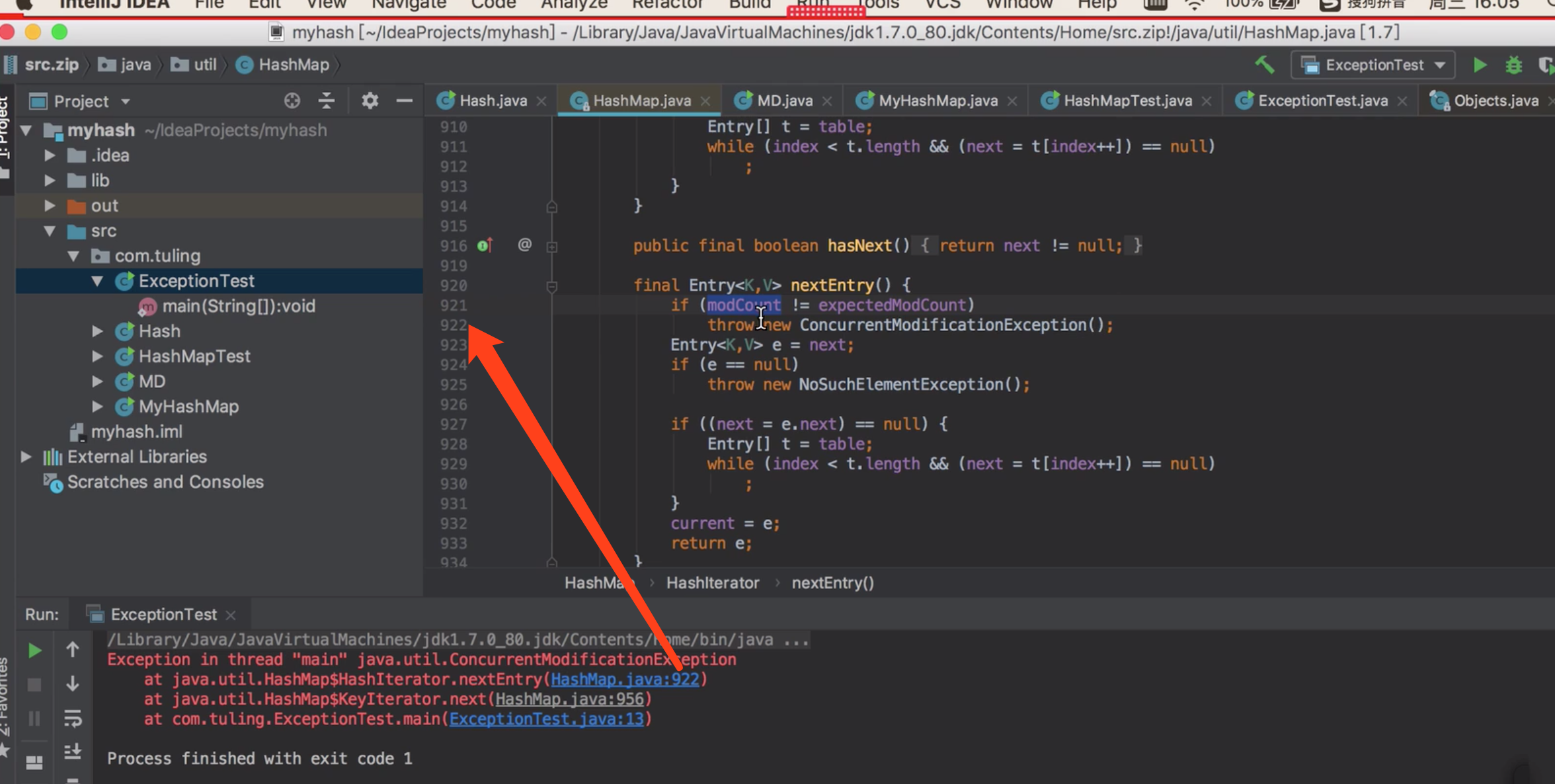
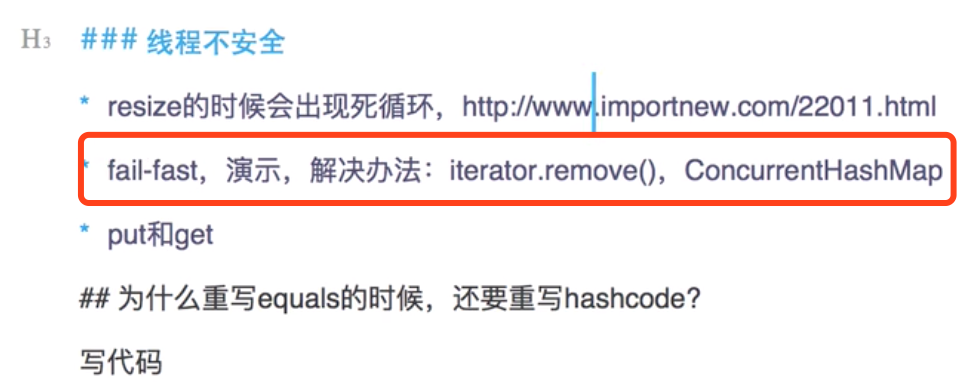
在多线程下面会有问题


e1, next1:线程1
e2, next2: 线程2

线程1挪完之后
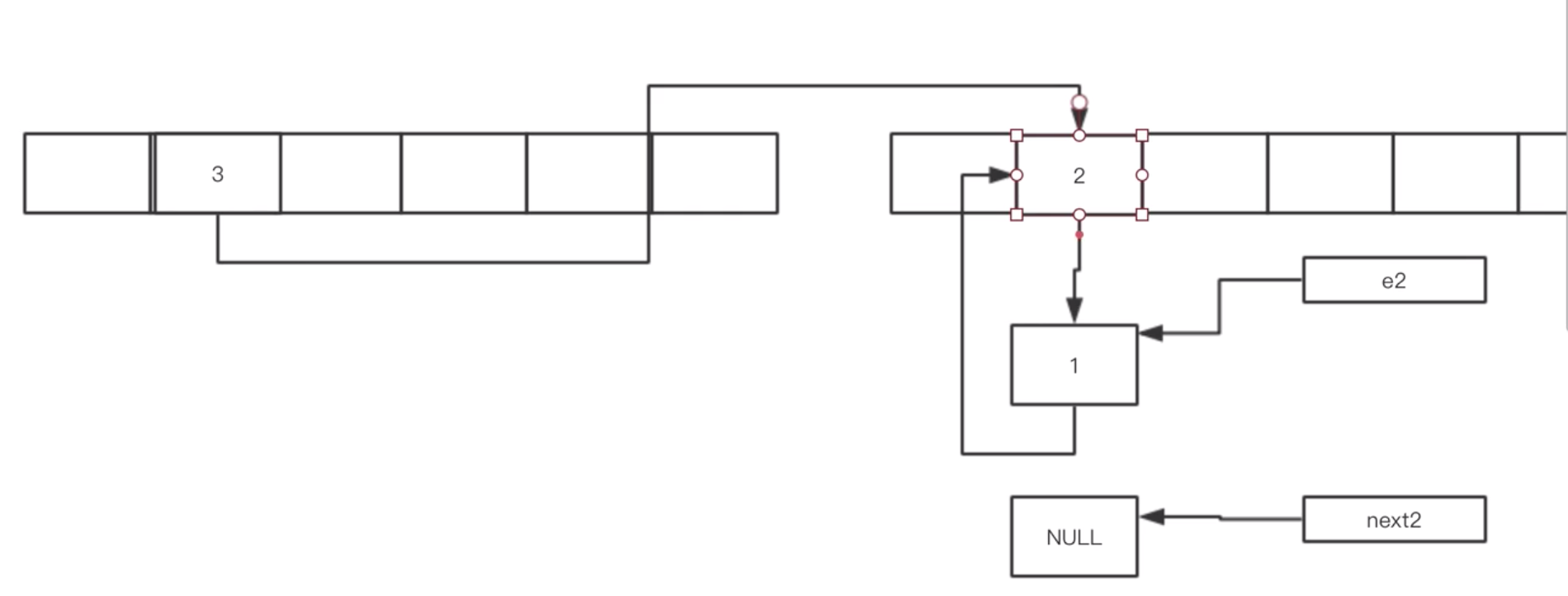
出现循环列表
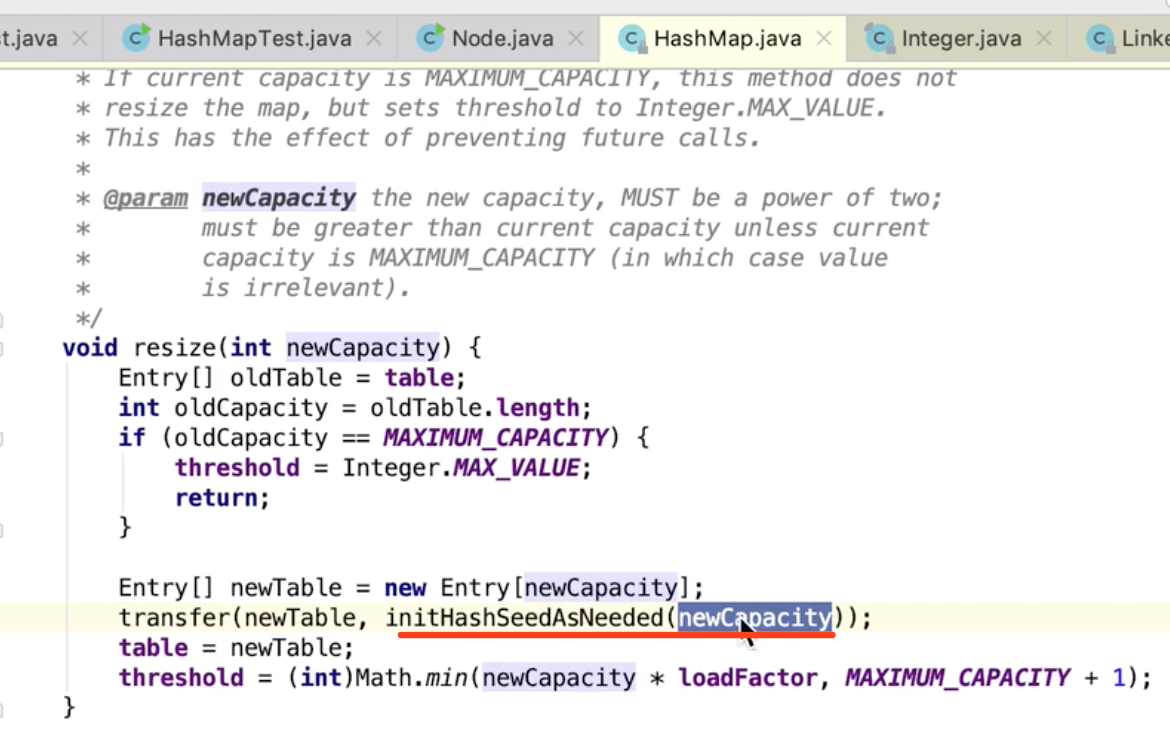

关键这句实际上是 Integer.MAX_VALUE
极少有 rehash 的情形发生

扩容会有循环链表的情况发生。。。

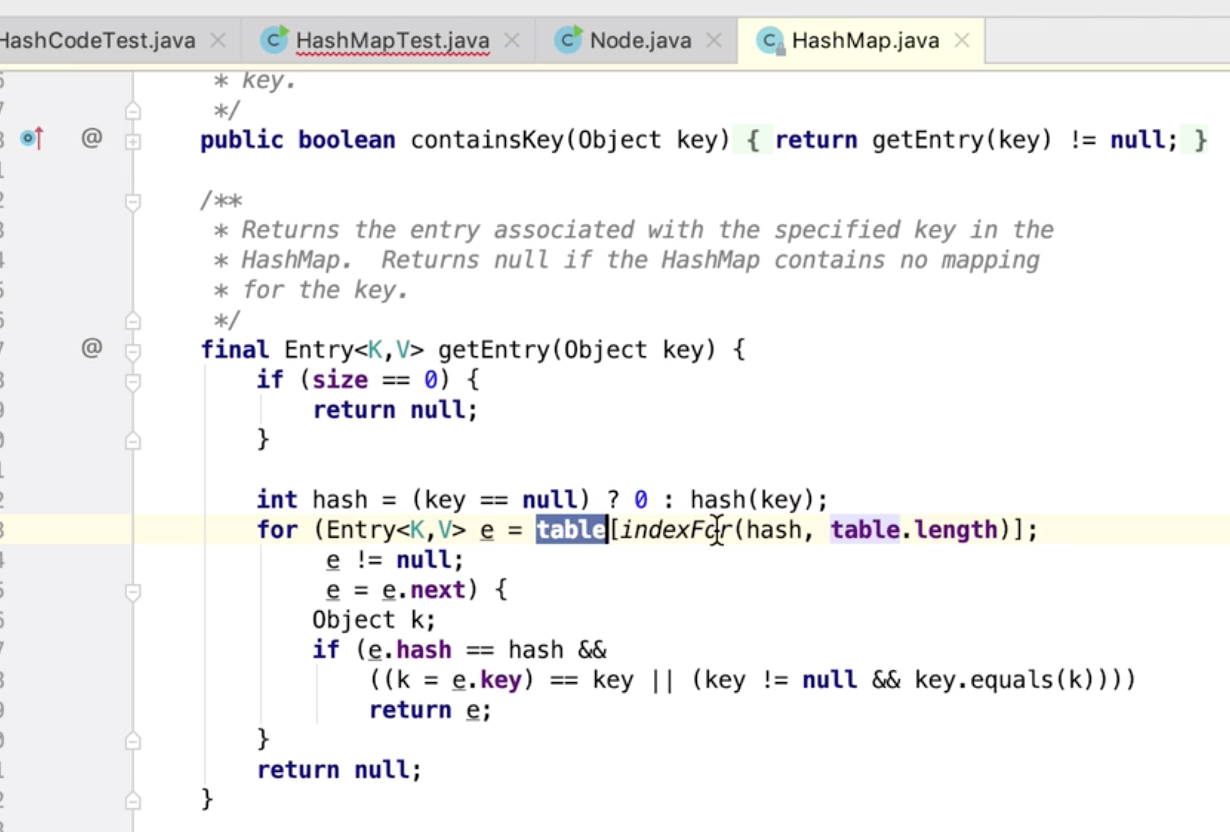
key为null 的时候怎么做呢?

如何变线程安全——直接加锁,这就是HashTable ,在每一个方法上面都加 synchronized
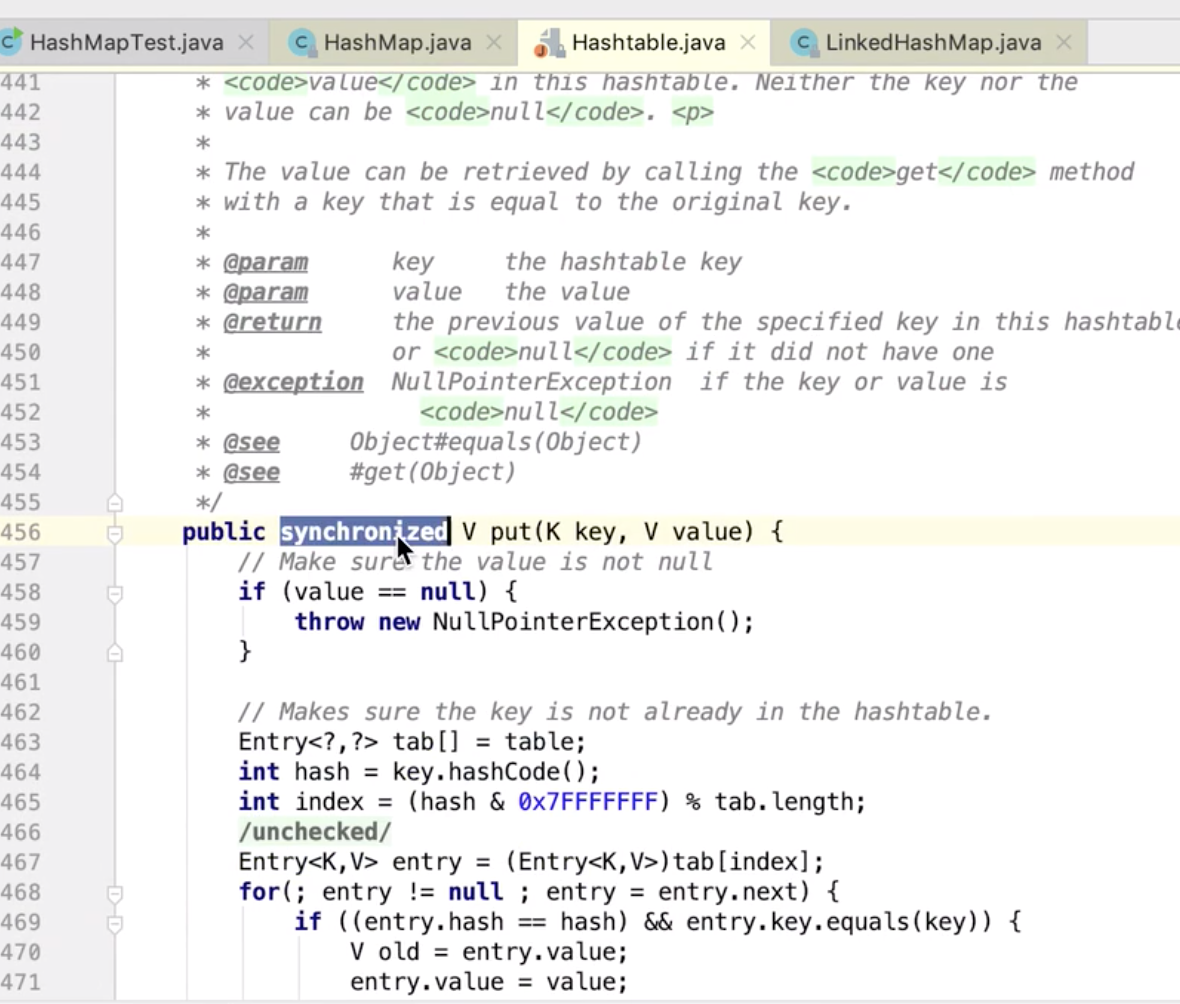
分段加锁
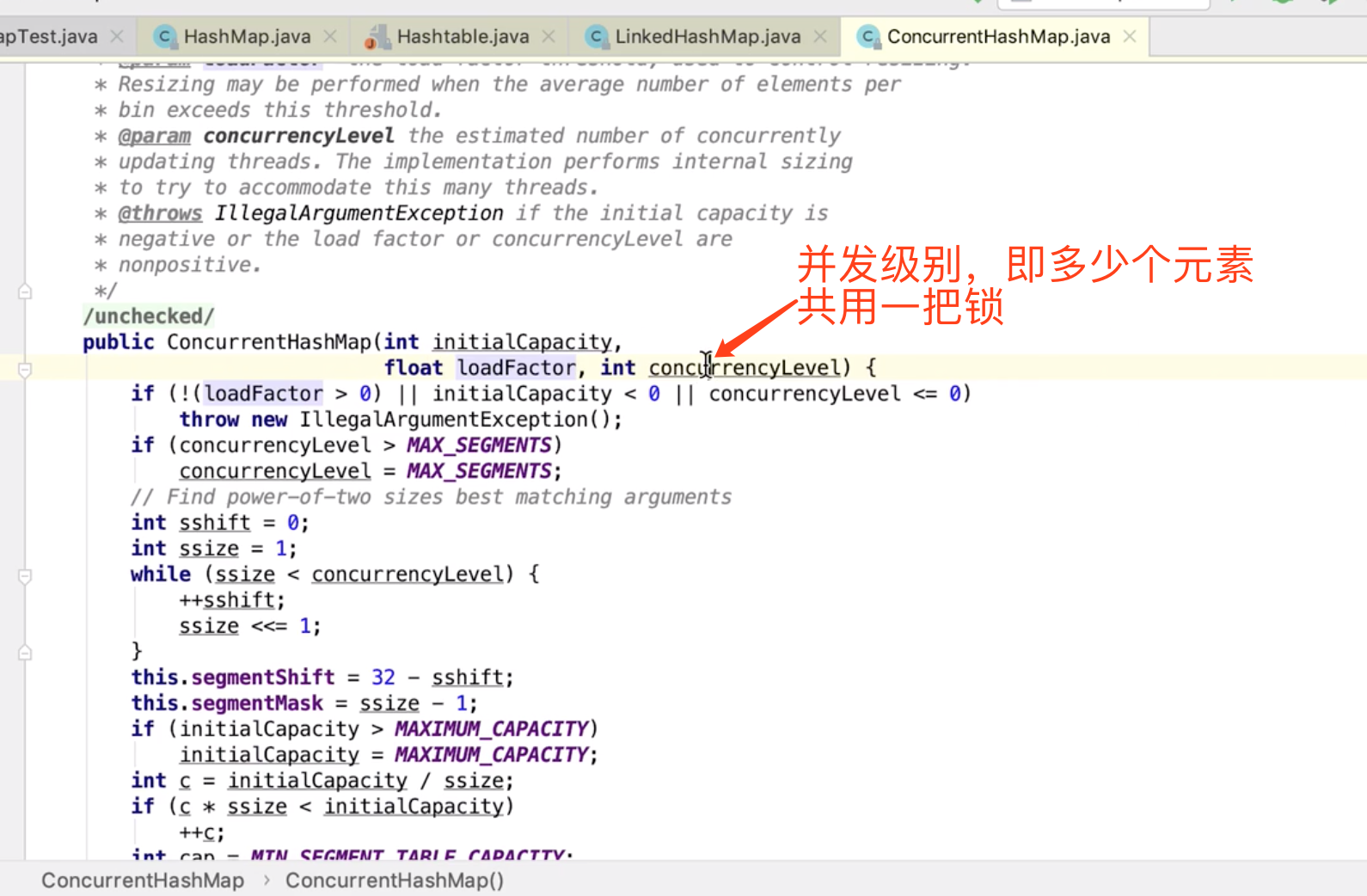
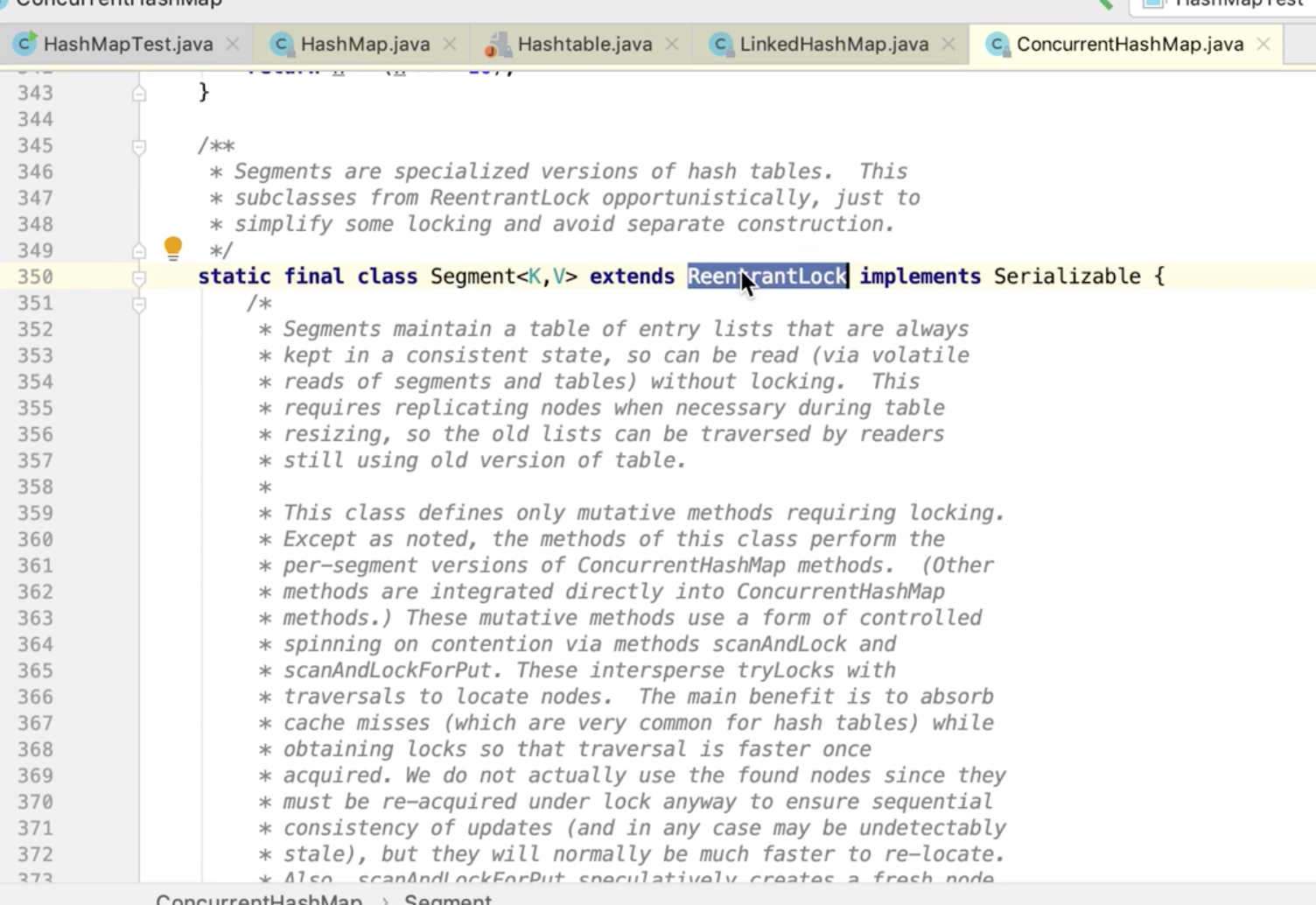
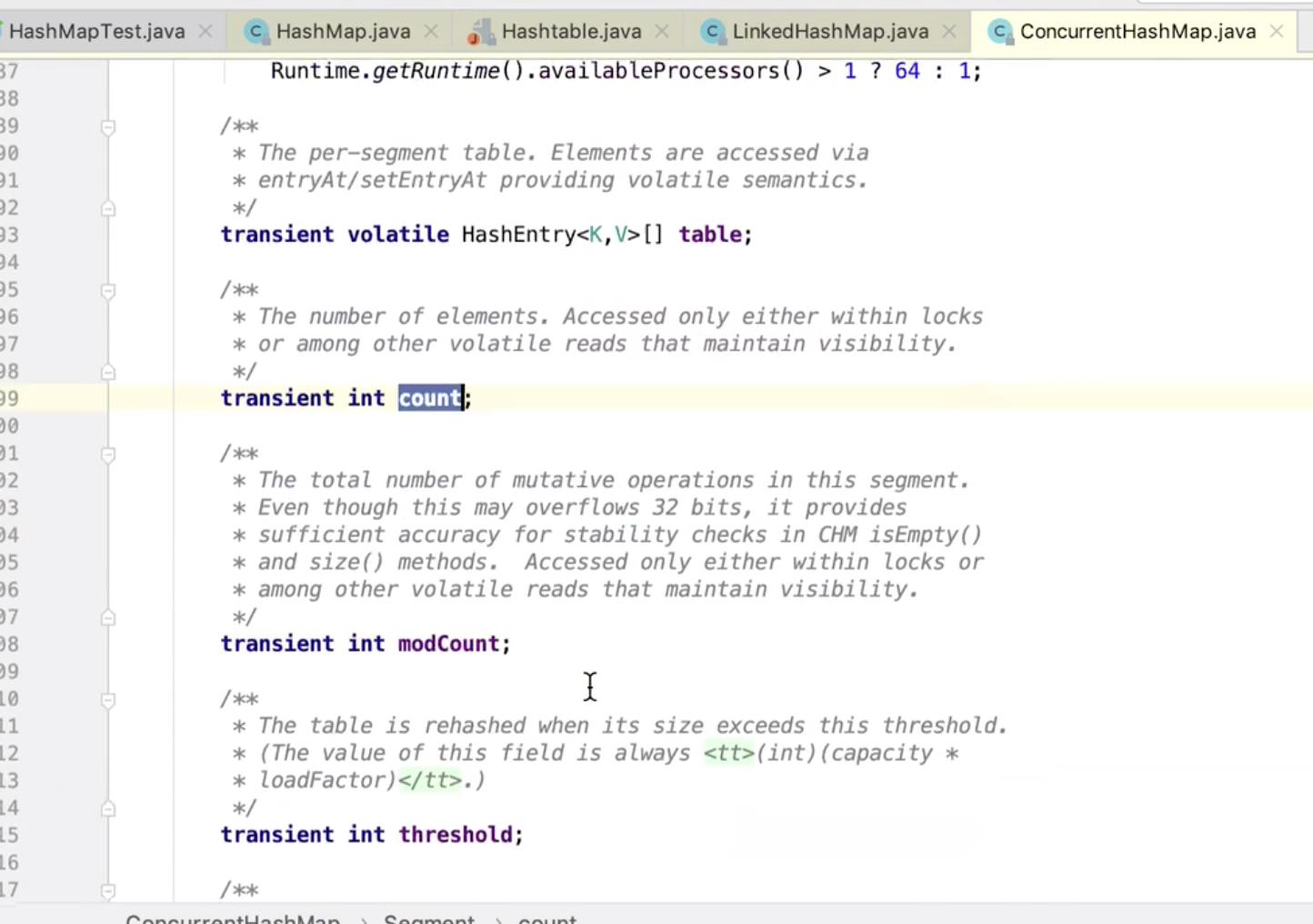

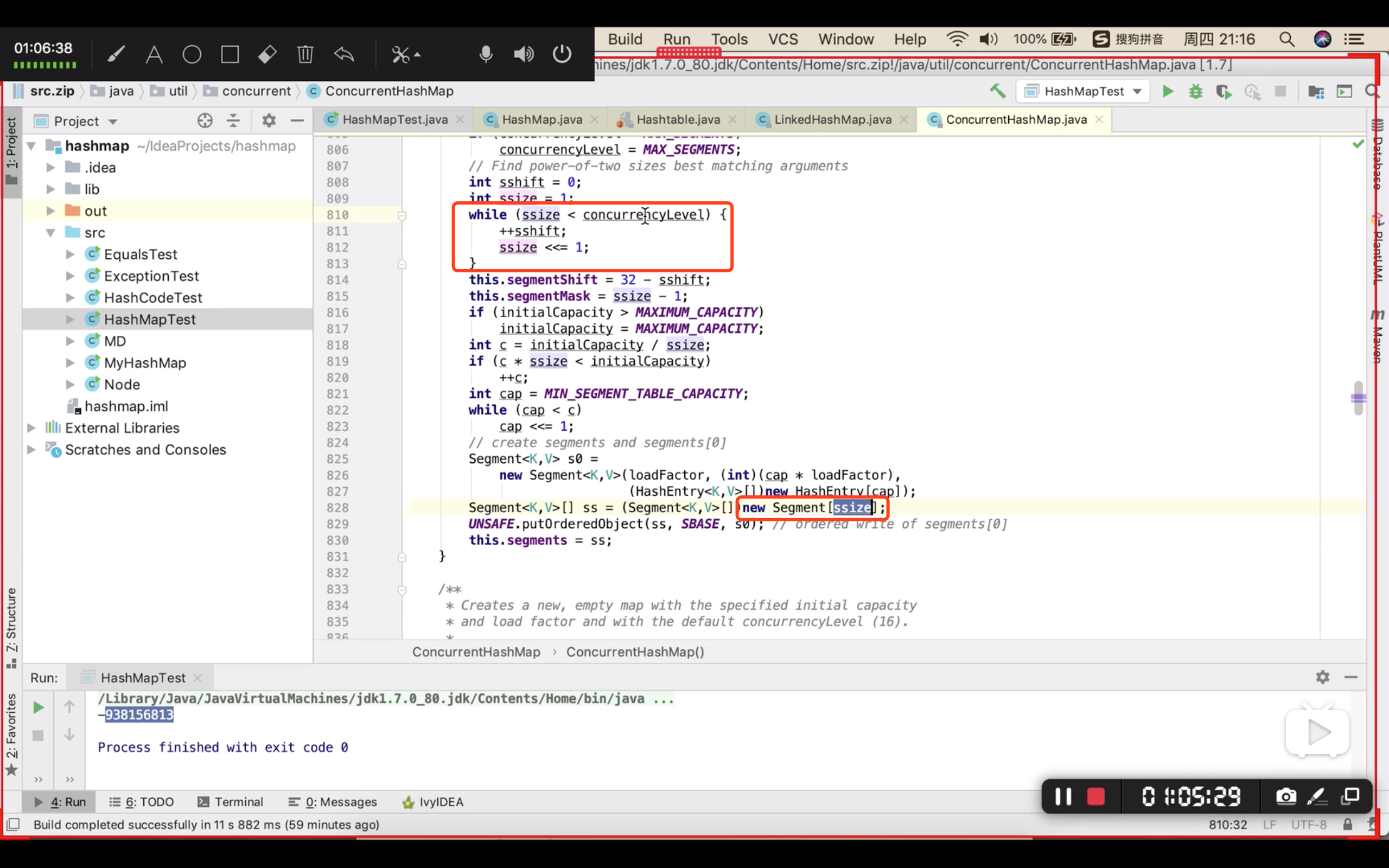
并发级别:不是多少个元素共用一把锁
不是用来确定 小 HashMap 的长度
而是用来确定 有几个 HashMap (大于 并发级别 这个数值 的最小2次方)。。。

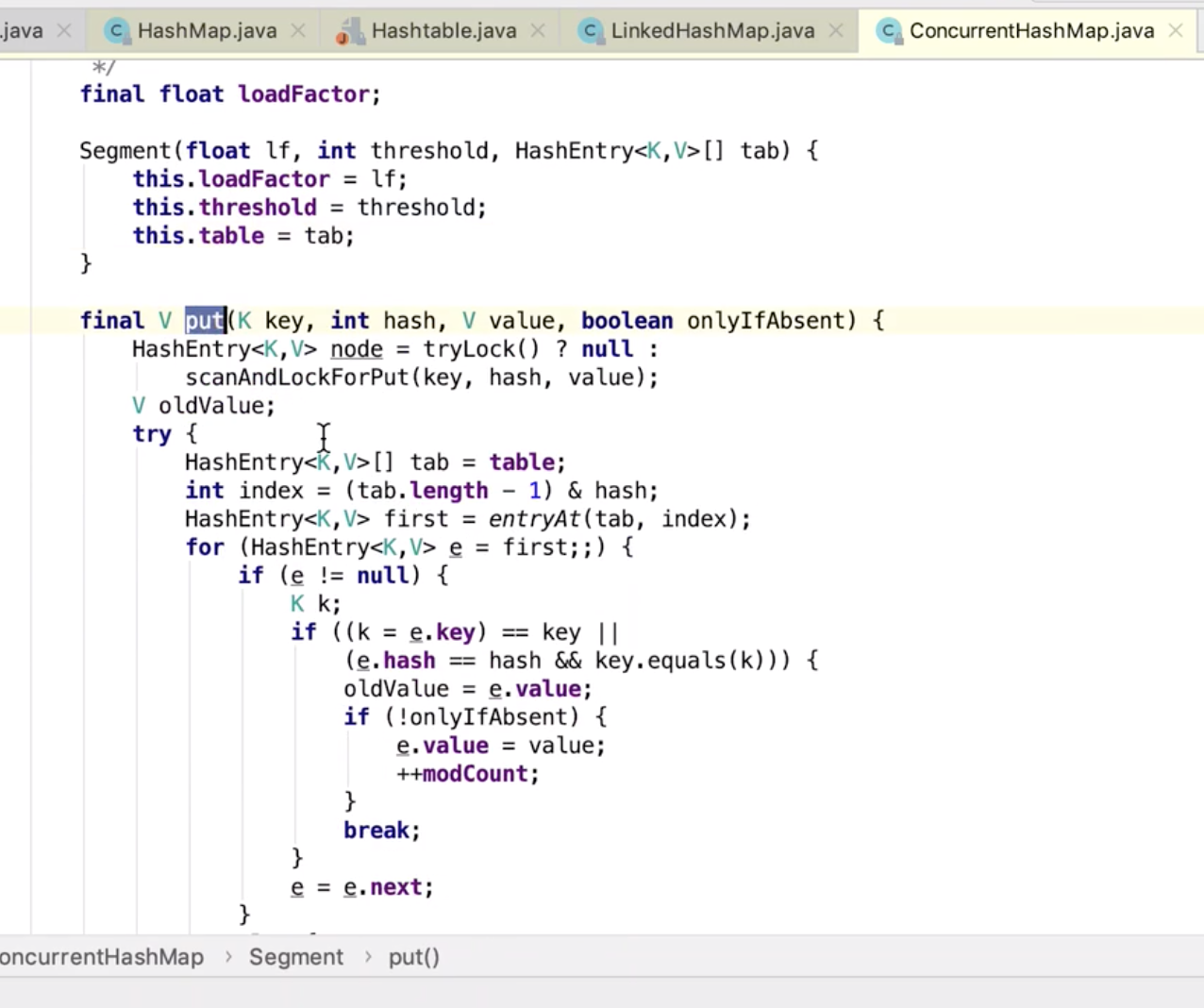
Segment put
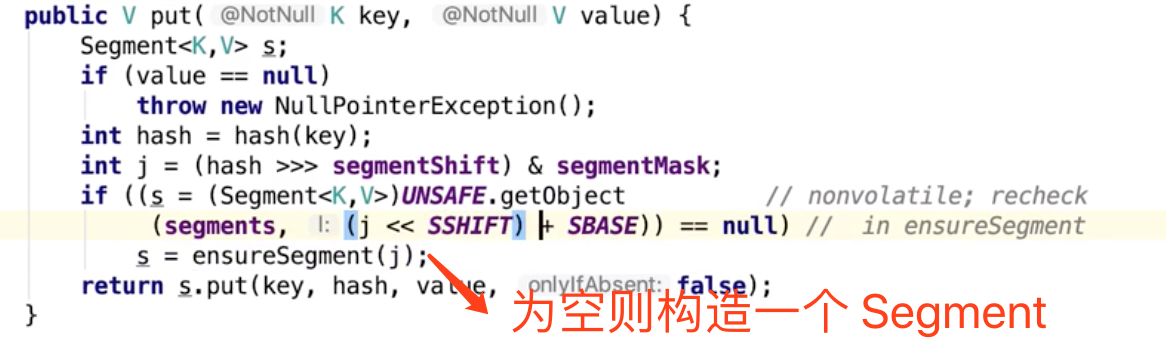
UNSAFE 能保证并发安全

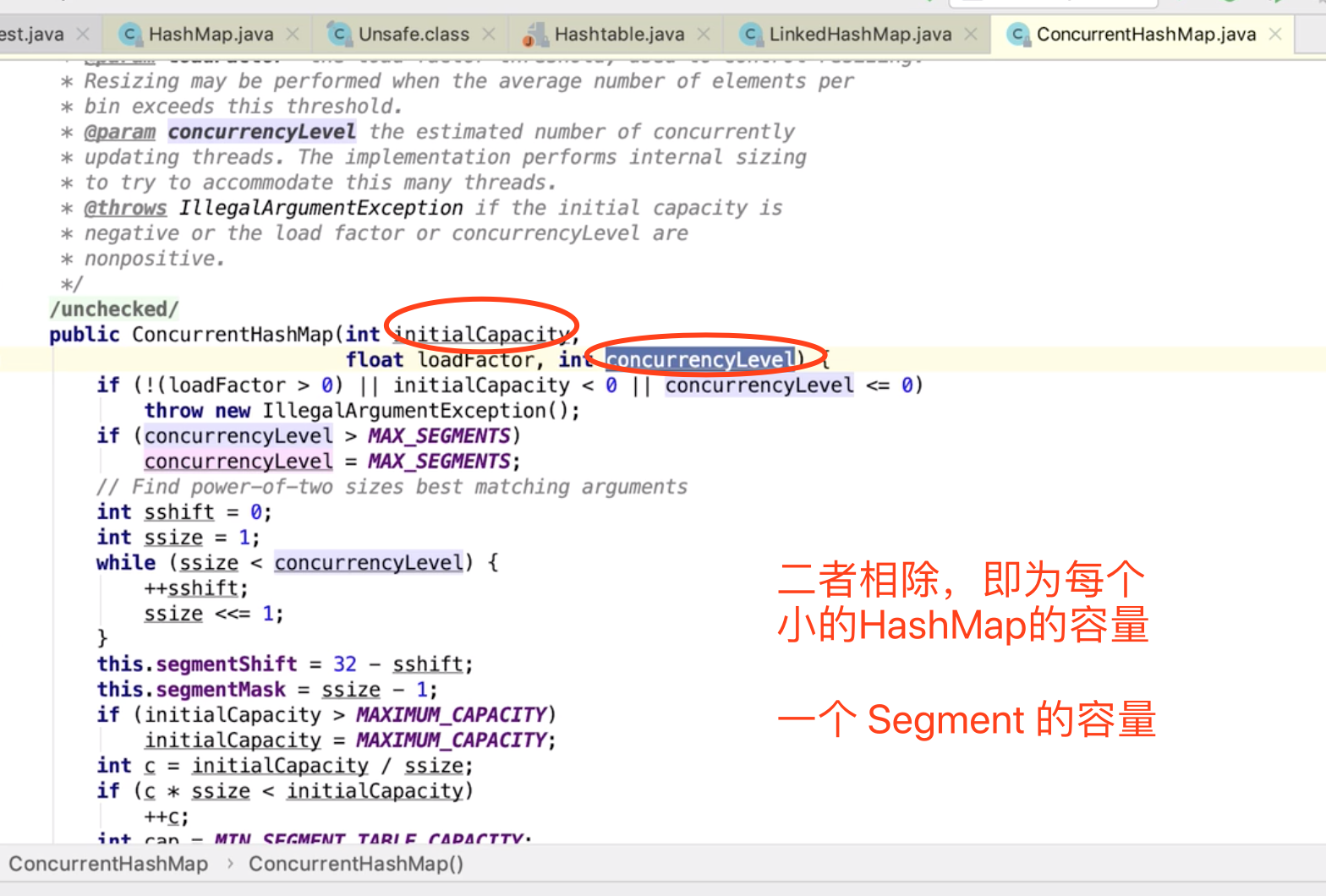
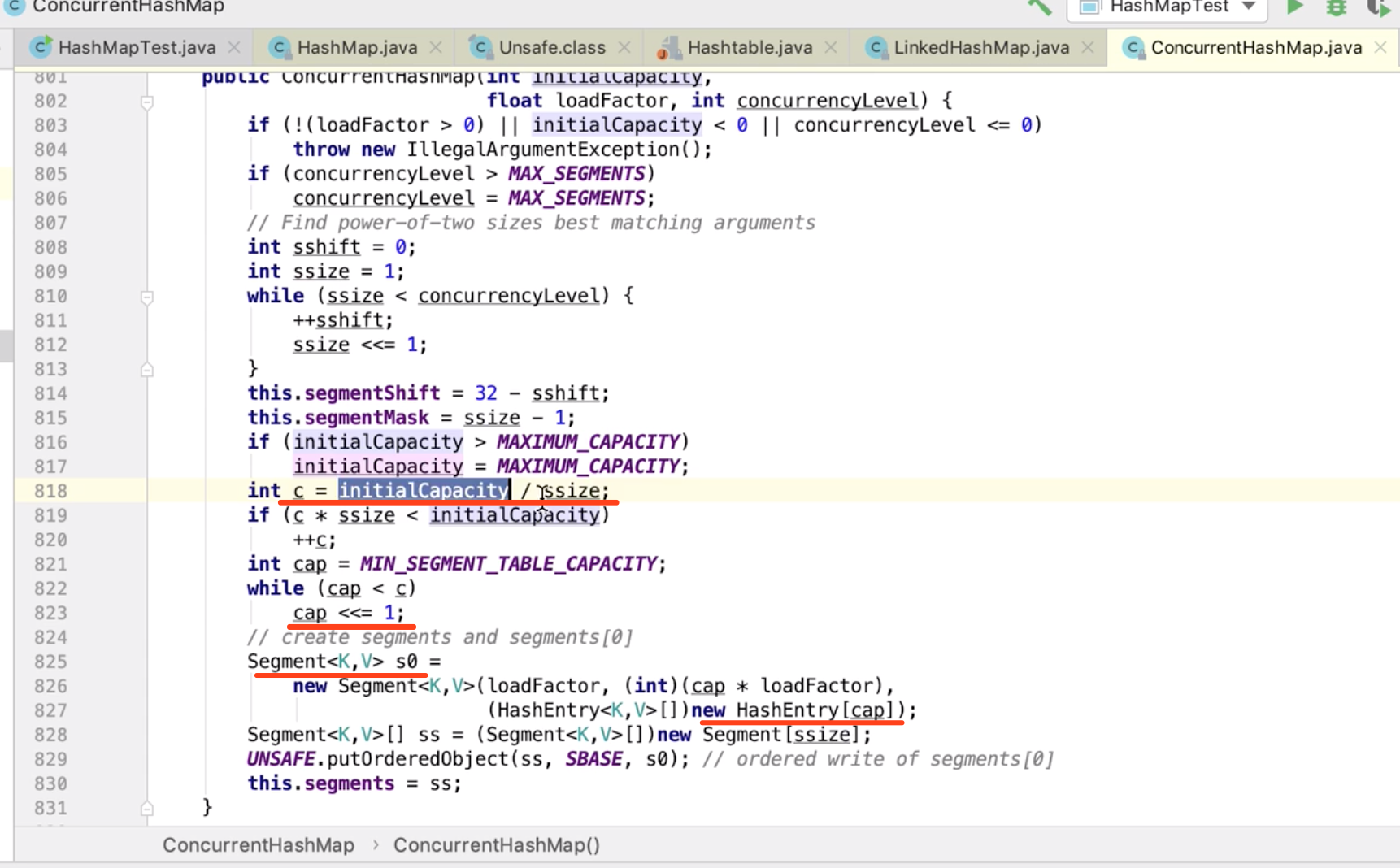

这段代码逻辑实际上简单的
写这么多主要是为了 并发安全 CAS 啥的
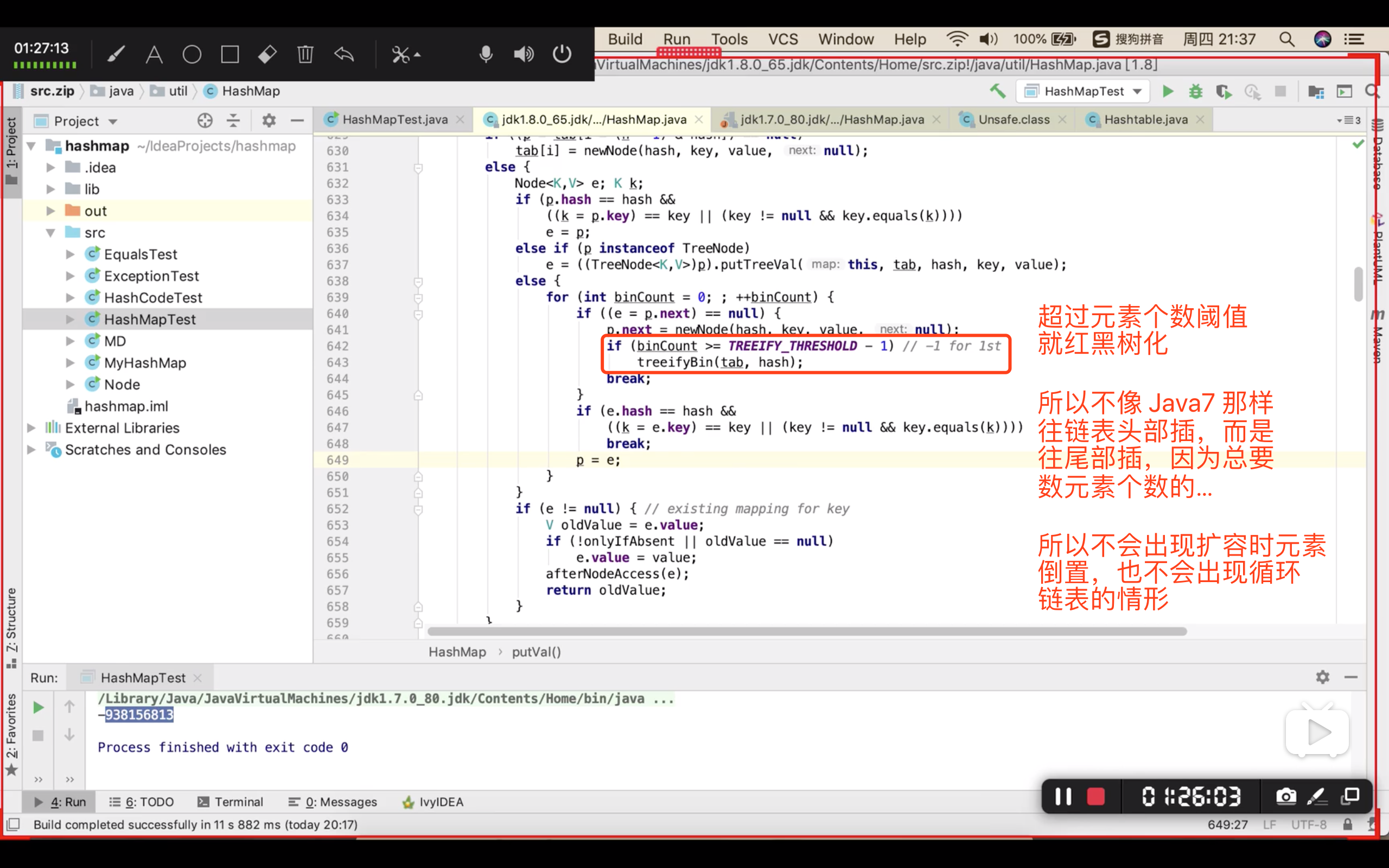
Java8:HashMap 的 链表改成 红黑树