非线性泛函分析导论(一): 变分法与 Sobolev 空间
1. 引言
本系列文章旨在介绍【非线性泛函分析】的一些入门、导论性质的知识。读者只需要具备本科层次复变函数、实变函数、数学物理方程、线性泛函分析、微分几何的基础就可以阅读了。如果学过了古典变分法那就更好了(以上这些内容在非线性泛函分析中都会用到)。鉴于本科泛函分析大都没涉及 Sobolev 空间的知识,或者说涉及的比较少,因此在正式学习非线性泛函分析之前,还是有必要补充一下有关内容。
我们在学习【偏微分方程】、【微分几何】或者【最优控制理论】的时候都接触过【古典变分法】。我们知道,古典变分法与泛函极值问题基本是同义语,并且在那时,我们总是假设泛函定义在连续可微函数空间上。显然,不论对于理论研究还是实际应用而言,这样的假设太强、太苛刻了,并且连续可微函数空间的很多性质都非常差。现在,我们想在一个性质好得多的空间上施展变分法,这个空间必须像连续可微函数空间那样,把函数和它的各阶导数容纳进来。为此,我们引入:

为什么我们需要拓展经典导数?且看下面这个例子:
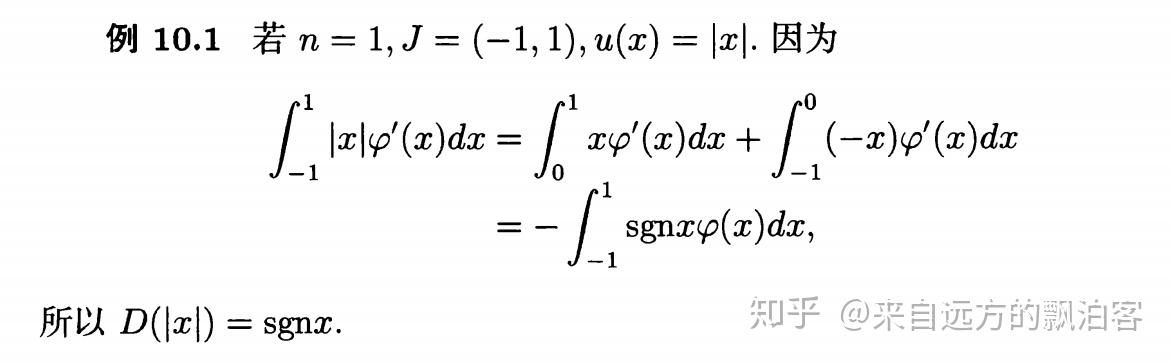
什么是导数?导数衡量的是变化率。但是例 10.1 中的函数用经典导数刻画不了函数在零点的变化率,而广义导数可以。
从此以后,我们说导数(不加前缀)都是指广义导数。原来数学分析中的导数我们称为 “经典导数、古典导数”。

简单地说,Sobolev 空间中的函数是这样的函数:它,连同它的直到 m 阶导数都属于 L^p 可积函数。
对于 Sobolev 空间,我们特别强调如下两个结果:
1.Sobolev 嵌入定理

我们简要谈一谈对这个定理的理解:给定 Sobolev 空间中的一串收敛序列,那么它们在 L^r 空间中按照 L^r 范数同样收敛。这是其一。
其二,对于 “连续嵌入” 四字的理解,分析上可以得出一族重要的积分不等式:函数的 L^r 范数小于等于函数的 W^m,p 范数乘上一个常数!!!即
嵌入,本质上是把 W^m,p 中的一个元素恒同地放入到 L^r 空间中去,注意到恒同映射当然是线性的,根据本科泛函分析中线性映射的基本性质: 连续与有界等价即可得出这个不等式。
2.Rellich 紧性定理

这个定理对于偏微分方程、变分法来说是如此之重要,以至于再怎么强调都不过分!本文仅就变分法来谈一谈。我们知道,数学分析中有条 Weierstrass 定理是说:R^n 空间中,定义在有界闭集(紧集)上的连续函数必能取到最大值和最小值。但是对于一个定义在无限维空间上的泛函来说,这样的条件是不够的!事实上,对于泛函,紧集必须升级为弱紧集(弱紧集比紧集强,这个后面会说)、连续必须升级为弱连续(同理,弱连续比连续强!)才能保证泛函取到极值。紧嵌入定理在证明泛函的弱连续性、集合的弱闭性方面发挥着不可替代的重要作用。
如何理解这个定理?本科泛函分析里有条定理 Eberlein-Schmulyan 定理是说:自反 Banach 空间有界序列必有弱收敛子列。紧嵌入是指嵌入是紧映射,即:将有界集映射成列紧集。Sobolev 空间是自反空间,因此 Rellich 紧性定理无非是说,给定 Sobolev 空间中一串弱收敛序列,则它们在 L^r 空间中按范数收敛!!!
2. 可微泛函
为了直观理解非线性泛函,我们可以类比 n 维空间,把无限维的 Banach 空间想象成一个平面(Banach 空间是平直的),那么一个泛函的等直面可以用图表示:
当然,如果泛函的定义域是一个 Banach 流形,那么它就更加地,或者说彻底地没有线性性可言了!
为了处理非线性泛函,我们首先在无限维空间上引入相应的微分概念。


G - 微分和 F - 微分的概念基本就是数学分析中方向导数和微分的直接、平行推广。

如前文所说,弱连续比连续要强。∵ 只要 Xn 弱收敛,就要求 F(Xn) 强收敛!

如同数学分析一样,若泛函的极值点必然是临界点(微分拓扑中的概念,指导数为零或 Jacobi 矩阵退化的点,于泛函而言是指其 Frechet 导数为 0 的点)。同样的,我们也有约束泛函极值的 Lagrange 乘子定理:
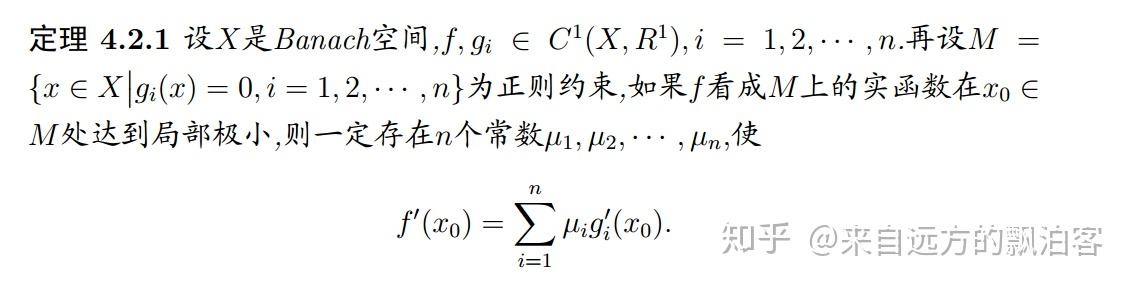
正则约束说的是约束条件的 Jacobi 矩阵非退化,从而构成一个流形。
我们试着求一个泛函的微分:
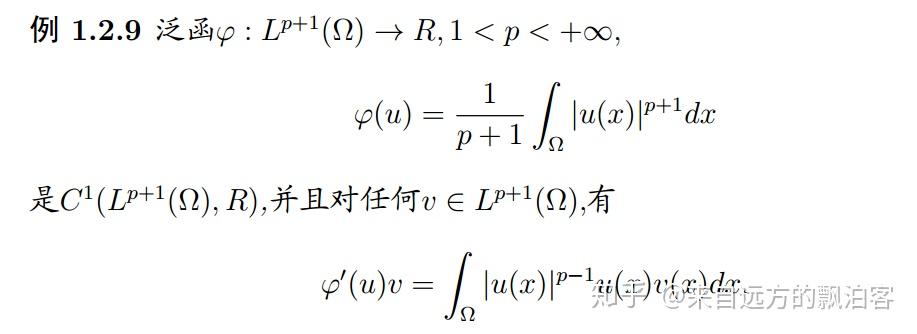
做法是不是很熟悉?事实上,这就是古典变分法里的做法!注意,
是一个由 u 决定的线性算子,作用在 v 上!!!(导射是线性映射)
3. 小综合
我们试着综合利用 F - 微分的概念、Lagrange 乘子定理和 Rellich 的紧嵌入定理来解决一个特征值问题。

令
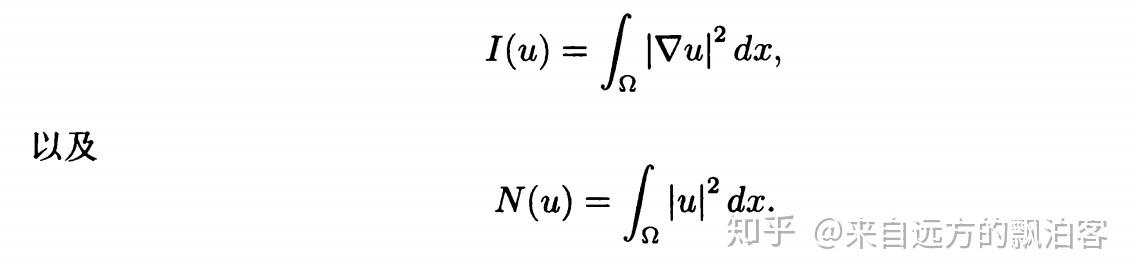

容易验证泛函 I(u)是弱下半连续的。为了证明问题 12.7 解的存在性,我们需要证明:
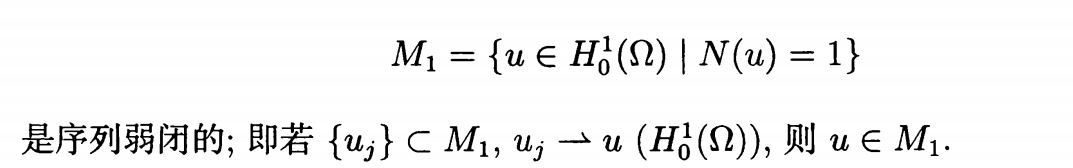

这一段如果不懂,回过头去再看一下我对 Rellich 紧性定理的解释!
4.Caratheodory 映射
在本篇文章的最后,我们简要介绍一下 Caratheodory 映射。这是一个测度论中的结果。它在证明泛函是
泛函时非常有用。



定理 2.1.14 非常重要,结合 Holder 不等式,我们可以证明许多泛函的可微性。下面是我分享的自己当年的非线性分析习题,读者可以凑合着看。


例题实在看得费劲的话,可以参考任何一本临界点理论的书籍。
5. 小尾声
通过本文的铺垫,我们大致对变分学有了一个基本的了解。但这还不够!我们离所谓的大范围变分法尚有很大的距离!!!(Boss 终于浮出了水面)
所谓大范围变分法,是指直接根据泛函的性质和定义域(一般是一个 Banach 流形)的拓扑性质判定泛函的临界点的存在性!(这直接对应拟线性或非线性偏微分方程解的存在性)为此我们需要引入大量代数拓扑和微分拓扑的知识,其中包括拓扑度 / 映射度,以及畴数理论、同调论和 Morse 理论等等。因此……
to be continued
下回预告: 可微泛函的 Palais-Smale 条件与 Ekeland 变分原理,拓扑学预备知识: 映射度与流形的环绕
心急的同学可以先行参看:米尔诺《莫尔斯理论》、张恭庆《临界点理论及其应用》
之后会讲到 Bocher 积分吗?或者说 Bochner 积分在这方面会用到吗
我会考虑的。不过我还是想把大范围变分法里的一些最基本的定理讲完再说。另,你是研究金融数学的么?
不是,我只是对随机分析比较感兴趣
感觉广义导数的定义不唯一,可以相差任意一个支集是零测集的函数。
相差零测集的函数放在 L^p 空间是不区分的
eg1.2.9 仍是连续泛函求导啊
泛函对自变函数 u 求导,没错啊。一般多元函数求导是对自变量 x 求导。
如果 fi 是不连续的泛函,应该怎么求导呢?
作者希望能少一点张恭庆老师书上的东西。
你是不是想看偏应用的? 如果是的话,下篇就是
实话实说,并没有看到让人耳目一新,有价值的东西!还不如直接贴些你当初的考试题目,习题来的有用!
感谢您,这篇文给我的帮助很大,可以跟您请问文章中的引用是来自哪本书吗?感恩您
临界点理论及其应用
题主能推荐一本比较好的讲非线性泛函分析的书吗?我是大四在读,即将要去读博,做计算力学,以后可能会用到,谢谢题主
求作者推荐一本可读性较强的非线性泛函分析教材
注册会计师的数学水平好高啊
第一个公式为什么成立呢?
大神,distribution derivatives 这个是啥意思啊,是广义导数吗
全文完