强化学习传说：第五章 基于模型的强化学习
Hello，大家好，这里是糖葫芦喵喵~！
说道夏天，当然就是各种各样的西瓜和冰激凌啦，快抱起你爱吃的食物来迎接伯克利强化学习CS294 最后一期内容吧！
本期内容：Model Based Reinforcement Learning (CS294 hw4)
推荐阅读：Berkeley CS294-112 深度增强学习 笔记 (9) 用数据拟合模型
喵喵的代码实现：
https://github.com/Observerspy/CS294那么，继续我们的强化学习旅程吧~！
Part 1 Model Free & Model Based
首先让我们回顾一下前面几期的内容：在模仿学习中我们试图从获取的大量的数据（输入观测o，输出动作a）中进行学习，最终得到一个策略网络：这样的方法由于实际数据和训练数据分布不一致往往很难取得效果。然后我们尝试使用动态规划（值迭代、策略迭代）、蒙特卡洛(MC)以及时间差分(TD)三种方法来解决马尔可夫决策过程描述的强化学习任务。其中动态规划虽然只bootstrapping一次但需要知道环境转移模型，而蒙特卡洛虽然无需知道环境转移模型但每次都要一个完整的episode，因此结合了两者的时间差分就显得非常有效。我们在DQN中进一步将时间差分中的Q-learning和深度学习结合构建价值网络，训练了一个非常有趣的能打pong游戏的agent。随后我们从直接最大化回报函数的角度，学习了策略梯度方法，它将策略网络和价值网络相结合，发展出了著名的Actor Critic算法。
在这么漫长的学习旅途中，我们发现我们的算法越来越复杂，训练难度以及耗时越来越大。怎么解决这个问题呢？
那就回到原点吧！我们第一个有效的方法是动态规划，在诸多方法中非常快捷。但是，它有一个缺陷，那就是必须要知道环境的状态是如何转移的，即需要基于模型。而其他方法无需知道这个环境模型，因为本质上，这些无模型的方法是通过agent不断探索环境，不断试错，不断学习，因此导致了无模型的方法数据效率不高。而基于模型的方法则相反，它能够充分利用已有的模型，高效地利用数据。
那么我们很自然的就会想，不如我们先学一个环境的模型吧！
于是新的问题就来了，环境怎么建模？例如怎么对一个游戏建模？怎么对自然语言处理问题建模？
是不是感觉无从下手？幸运的是有些问题是可以建模的，例如机器人控制，机械的运动都是符合物理规律的，因此这类问题可以很好的建立运动模型。而如果我们很好地学习到了这些运动模型，我们甚至可以将这个模型泛化到其他的机械控制问题中。因此基于模型的方法往往会有比较好的泛化能力。但对于不同的环境就不能通用了，这也是无模型方法的通用性优势所在。
Part 2 Model Based RL
前面说了很多基于模型方法的好处，那么究竟怎么来学习一个好的模型呢？
来看我们的目标：学习环境的状态转移模型，也就是我们希望知道 的下一个状态
是什么。那么我们就获取这样的数据来学习（输入
，输出
）。也就是我们学习一个模型
，使得它和
之间的误差很小。然后根据这个
可以采用动态规划或者最优控制等方法来进行计划(plan)（最优控制中的轨迹优化等方法比如iLQR可参考引导策略搜索方法（GPS）中的轨迹优化_LQR）。这样我们就有了一个基础的基于模型的学习方法：
1. 通过某种策略 例如随机策略来获取大量数据
2. 学习一个模型 来最小化误差
3. 运用模型 来进行计划
嗯？这个框架是不是在哪里见过？这个和强化学习传说：第一章 模仿学习中的Behavioral Cloning不是一样的嘛。所以他们的问题也一样，训练数据和我们执行计划后的实际数据分布不一致啊。那我们在模仿学习中是怎么做的？对，DAgger！我们把新获取的数据加到原来的数据里进一步训练就行了。
1. 通过某种策略 例如随机策略来获取大量数据
2. 学习一个模型 来最小化误差
3. 运用模型 来进行计划
4. 执行计划获得新数据，并将新数据加入到D中回到步骤2
注意这个方法和DAgger的不同：这里我们的目标是学习模型，而DAgger是学习策略。
还不够好。为什么呢？
因为我们的模型总是不可避免地存在模型误差。我们在存在一定误差的模型基础上进行对未来的计划，一定会造成误差不断积累最终产生巨大的误差。
下面我们采用模型预测控制（Model Predictive Control,MPC）来使我们的模型更好一些。
Part 3 Model Predictive Control
模型预测控制本身应该属于控制理论的内容，是一种闭环控制方法，喵喵不在这里班门弄斧了，大家可以看看这个问题：预测控制简单来说到底什么意思？。
我们来举个例子简单说明一下：
1. 设想我们要完成一个任务，任务在上午8点开始。
2. 我们每次做未来N个小时的计划(plan)，但只在第一个小时实施该计划。
3. 我们不断进行这个过程，直至任务被完成。
结合我们的场景，也就是说现在我们学习了一个模型 ，然后根据模型可以采用iLQR等轨迹优化的方法来对未来做计划。但是每次我们只执行计划中的第一步来获取新的数据。具体流程如下：
1. 通过某种策略 例如随机策略来获取大量数据
2. 学习一个模型 来最小化误差
3. 运用模型 来进行计划
4. 执行计划第一步获得新的一条数据
5. 重复步骤3-5若干次，将获取的新数据加入到D中回到步骤2
模型预测控制本质是通过不断重新计划来使得错误累积不会太多，我们重新计划的次数越多，那么我们每一个计划的精度要求就可以降低一些。因此我们可以采用一些简单的方法来进行计划，从而降低我们的计算复杂度。
我们本次的作业就是要实现MPC这样的一个基于模型的强化学习方法。
Part 4 Algorithm and Implementation
下面我们就来实现这个方法。
首先根据上面讲到的流程，我们先要通过运行某种策略来获取一些数据，我们就先用随机策略来获取数据：
data = sample(env, random_controller, num_paths_random, env_horizon)这个sample一共四个参数，分别是env：环境；random_controller：策略（随机）；num_paths_random：获取的rollouts(episode)的数量；env_horizon：每个rollouts(episode)最长步数。其实就是要我们在环境env中执行random_controller策略，每次最长env_horizon步，一共获取num_paths_random个rollouts(episode)。代码实现就是基本的强化学习套路：
for _ in tqdm.tqdm(range(num_paths)):# 循环num_paths次
# 初始化环境和参数
ob = env.reset()
obs, next_obs, acs, rewards, costs = [], [], [], [], []
steps = 0
while True:
obs.append(ob)
ac = controller.get_action(ob) # 执行策略获得动作(其实是self.env.action_space.sample())
acs.append(ac)
ob, rew, done, _ = env.step(ac) # 执行该动作获得下一状态、回报值
next_obs.append(ob)
rewards.append(rew)
steps += 1
if done or steps >= horizon: #当episode结束或超过horizon步后结束这个episode
break
path = {"state": np.array(obs),
"next_state": np.array(next_obs),
"reward": np.array(rewards),
"action": np.array(acs)}
paths.append(path)好了现在我们有了一些数据，然后对这些数据计算normalize所需要的参数：
normalization = compute_normalization(data)这个函数具体就是计算 、
和
的均值与标准差，这里不再赘述。
然后就到了第二步，可以把数据喂给神经网络去训练 了。这个网络在dynamics.py中，其实就是简单的FC层的堆叠。注意这个网络是用来拟合
的而不是直接输出
。也就是说，我们的输入是
和
，输出
。我们先在init中初始化一些参数：
# 上面计算好的normalization传进来
self.mean_s, self.std_s, self.mean_deltas, self.std_deltas, self.mean_a, self.std_a = normalization
self.sess = sess
self.batch_size = batch_size
self.iter = iterations
self.s_dim = env.observation_space.shape[0]
self.a_dim = env.action_space.shape[0]
# 状态-动作placeholder(None,s_dim,a_dim)以及(s_{t+1} - s_t)的placeholder(None,s_dim)
self.s_a = tf.placeholder(shape=[None, self.s_dim + self.a_dim], name="s_a", dtype=tf.float32)
self.deltas = tf.placeholder(shape=[None, self.s_dim], name="deltas", dtype=tf.float32)
# 输出预测
self.deltas_predict = build_mlp(self.s_a, self.s_dim, "NND", n_layers=n_layers, size=size,
activation=activation, output_activation=output_activation)
# loss
self.loss = tf.reduce_mean(tf.square(self.deltas_predict - self.deltas))
# AdamOptimizer
self.train_op = tf.train.AdamOptimizer(learning_rate).minimize(self.loss)下面就来把第一步得到的data喂给这个网络，首先在fit中我们利用计算好的均值和标准差来normalize数据：
s = np.concatenate([d["state"] for d in data])
sp = np.concatenate([d["next_state"] for d in data])
a = np.concatenate([d["action"] for d in data])
N = s.shape[0]
train_indicies = np.arange(N)
# normalize
s_norm = (s - self.mean_s) / (self.std_s + 1e-7)
a_norm = (a - self.mean_a) / (self.std_a + 1e-7)
s_a = np.concatenate((s_norm, a_norm), axis=1)
deltas_norm = ((sp - s) - self.mean_deltas) / (self.std_deltas + 1e-7)然后shuffle训练数据，将minibatch数据喂给网络：
for j in range(self.iter):
np.random.shuffle(train_indicies) # shuffle
for i in range(int(math.ceil(N / self.batch_size))):
start_idx = i * self.batch_size % N
idx = train_indicies[start_idx:start_idx + self.batch_size]
batch_x = s_a[idx, :] # minibatch x
batch_y = deltas_norm[idx, :] # minibatch y
self.sess.run([self.train_op], feed_dict={self.s_a: batch_x, self.deltas: batch_y})对于预测部分，我们在predict中还要对输出做一次denormalize，注意预测输出的是 ：
# normalize
s_norm = (states - self.mean_s) / (self.std_s + 1e-7)
a_norm = (actions - self.mean_a) / (self.std_a + 1e-7)
s_a = np.concatenate((s_norm, a_norm), axis=1)
# predict
delta = self.sess.run(self.deltas_predict, feed_dict={self.s_a: s_a})
# denormalize
return delta * self.std_deltas + self.mean_deltas + states这样回到main.py中我们就可以训练网络了：
for itr in range(onpol_iters):
dyn_model.fit(data)
...第三、四步中，我们要用这个模型做MPC，并通过MPC获取一些新的数据。
paths = sample(env, mpc_controller, num_paths_onpol, env_horizon)与随机策略不同，MPC每一步都先进行计划，然后只执行计划的第一步。也就是说sample函数中只有get_action不一致。这里MPC的get_action在controllers.py中。具体流程如下：
- 先用随机策略random出num_simulated_paths个最长为horizon的rollouts(episode)，注意执行每一步动作的时候用我们训练好的网络的预测作为下一个状（因为我们已经训练了一个环境模型）。
2. 评估这些rollouts(episode)，找到cost最小的那一条rollouts(episode)。
3. 返回cost最小的那一条rollouts(episode)的第一个动作。
下面的代码中使用了batch，可以直接同时对num_simulated_paths条待sample的rollouts(episode)进行后续计算，提高了算法的速度。（类似向量化）
ob, obs, next_obs, acs, costs = [], [], [], [], [] #(horizon, num_simulated_paths, n_dim)
# 初始化num_simulated_paths条rollouts的第一个状态
[ob.append(state) for _ in range(self.num_simulated_paths)]
for _ in range(self.horizon):
ac = []
obs.append(ob)
# 随机策略获取动作
[ac.append(self.env.action_space.sample()) for _ in range(self.num_simulated_paths)]
acs.append(ac)
# 利用训练好的模型输出下一个状态
ob = self.dyn_model.predict(np.array(ob), np.array(ac))
next_obs.append(ob)
# 计算num_simulated_paths条rollouts的cost
costs = trajectory_cost_fn(self.cost_fn, np.array(obs), np.array(acs), np.array(next_obs))
# 返回cost最小的rollouts第一个动作
j = np.argmin(costs, )
return acs[0][j]第五步，我们将MPC产生的新数据合并到原有数据中：
for itr in range(onpol_iters):
dyn_model.fit(data) #第二步
paths = sample(env, mpc_controller, num_paths_onpol, env_horizon) #第三四步
data = np.concatenate((data, paths)) #第五步好了，至此我们的算法就都实现完了。然后就可以在cheetah环境上对比random和MPC的方法了：
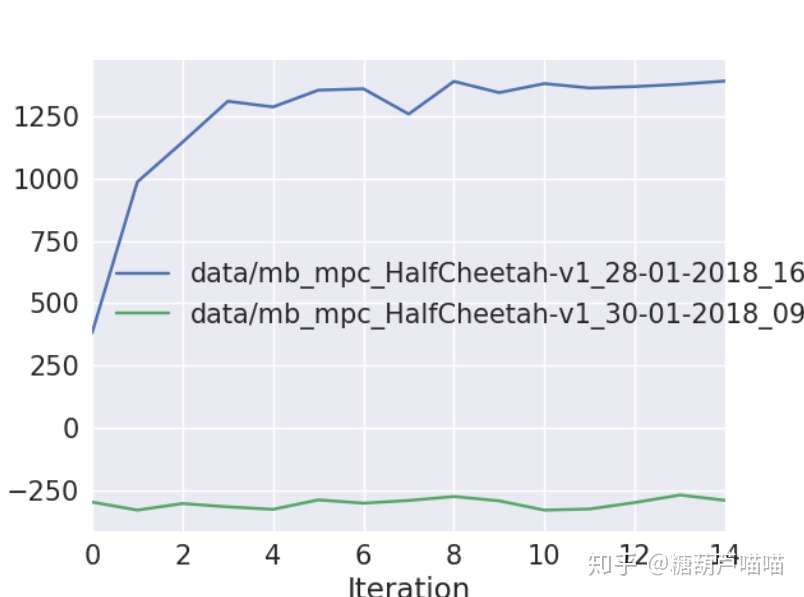绿色的是随机策略，蓝色的是MPC
可以看到在短短15个迭代过程中，MPC就达到了将近1400的平均回报。
我们可以继续调整网络结构、以及MPC中产生rollouts的策略，以获得更好的效果。大家可以多多尝试！
Part 5 backpropagate directly into policy
当然MPC并不是我们的万全之策。考虑无模型的方法，其本质是最大化回报函数。而我们的基于模型方法则是为了最小化模型误差。现在我们把两者结合在一起，试图通过回报函数来最小化我们的模型误差。
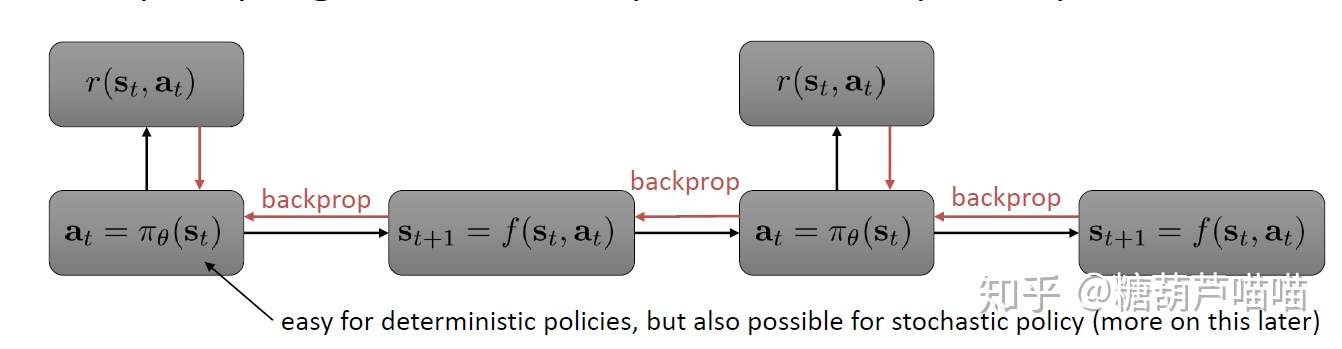
这个图很好理解：我们在状态 处根据策略
执行动作
，获得回报
，然后我们根据回报函数的梯度反向传播来优化策略
并执行，最终将获取的数据用来进一步优化我们的模型
...具体流程如下：
1. 通过某种策略 例如随机策略来获取大量数据
2. 学习一个模型 来最小化误差
3. 通过回报函数的梯度反向传播来优化策略
4. 执行策略 获得新数据，并将新数据加入到D中回到步骤2
这个方法有点类似RNN，因此RNN梯度爆炸、消失问题在这里也得到了继承。有一个简单的方法是把 用高斯过程来替换神经网络，这个方法就是PILCO：详见强化学习前沿 第三讲 基于模型的强化学习方法 PILCO及其扩展（一）
至此我们的强化学习作业解析就告一段落啦！基于模型的部分由于涉及很多控制论的内容，加之现在这一部分讲解的资料比较少，所以后面的部分喵喵也不是很理解，欢迎各位来一起讨论学习！虽然我们的讲解到此结束，但是我们的研究之路才刚刚开始！愿各位共同努力，推进技术的发展与进步。
では、おやすみ～！