【poor几何】[UVALive 6693]Flow Game计算几何，线代相交

【题目】
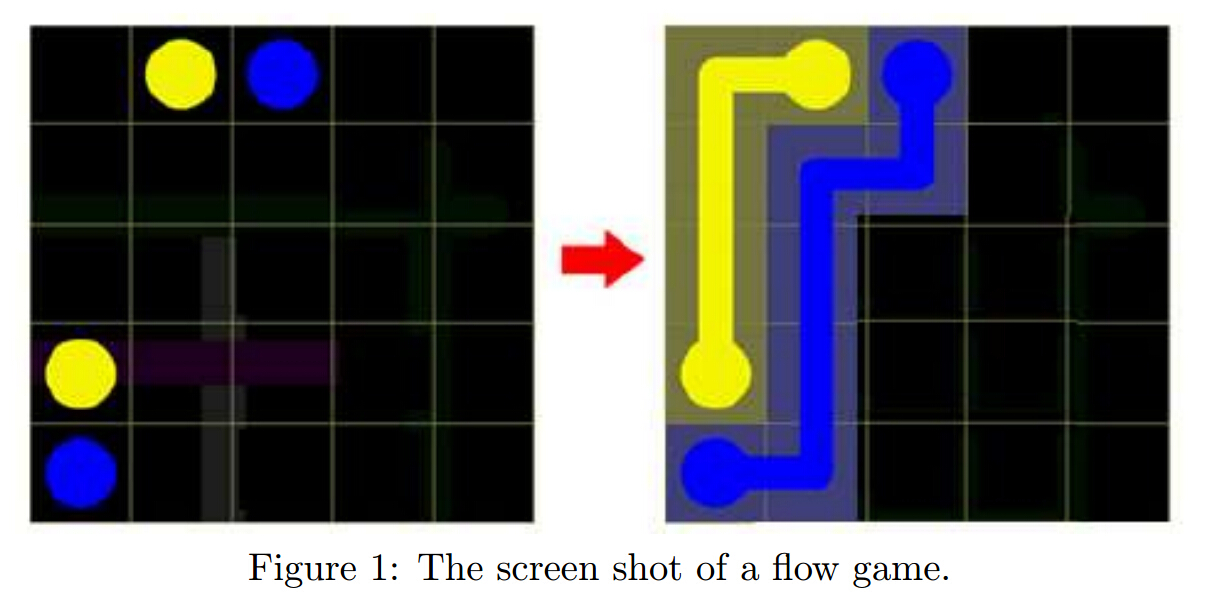
Flow game is a p opular game now on smart phone due to the invention of multi-touch screen. The rule of the game is easy. Given a b oard with N × N grids and given a set of paired color dots, please find a way to connect paired color dots without crossing the paths of others as in Fig. 1.

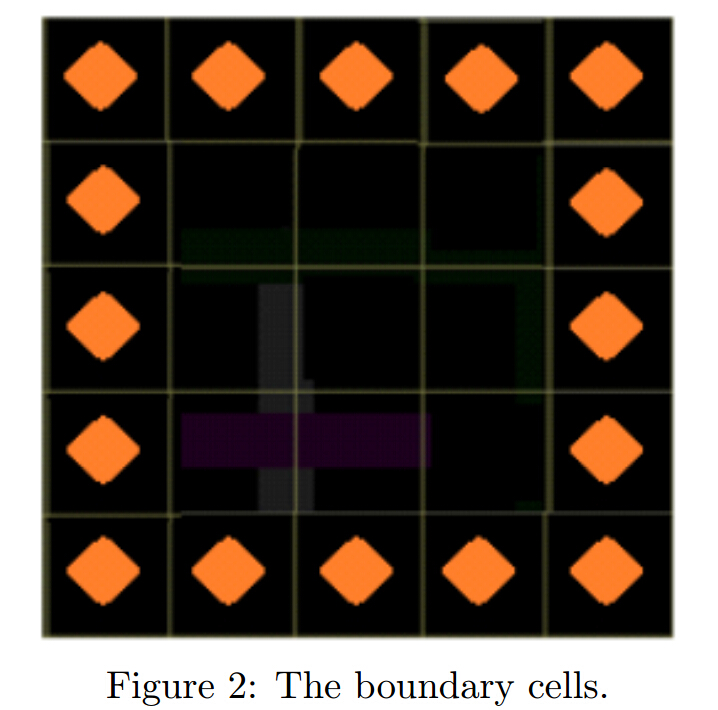
Fortunately, the flow games you need to solve only have two pairs of color dots and the color dots only app ear on the lo cations of b oundary cells. For example, Fig. 2 shows the boundary cells in a 5 × 5 grids.

Once you connect two pairs of color dots, there is a cost for your solution. The cost of your solution is the numb er of painted cells (including two end dots). For example, in Fig. 1, blue line paints 7 cells and yellow line paints 5 cells. So, the total cost is 12 which is minimum in this game. Given an N × N grids, please output the minimum cost to connect the color dots.

Input
The test data b egins with a p ositive integer T, which is the number of test cases. Each test case begins with a positive integer N ( N < 10), which is the size of the board. Following is N × N cells of board data. An empty cell is represented by a ‘ . ’. Color dots are described by ‘ 1’, ‘ 2’.

Output
Please output the minimum cost to connect the two pairs of dots. If there is no solution to a given game, please output ‘ -1’ in a new line.

Sample Input
2
5
.12..
…..
…..
1….
2….
5
.21..
…..
1….
2….
…..

Sample Output
12
-1

【题意】
给个棋盘，你可以在棋盘的边缘处放2个蓝色棋子2个黄色棋子，问连接2组同色棋子的最小代价，如果线路交叉，输-1。

【思路】
一般情况如果有解，则可发现两点连线最小代价=曼哈顿距离+1，所以一般情况：
ans=abs(X1-X2)+abs(Y1-Y2)+abs(X3-X4)+abs(Y3-Y4)+2;
判断-1：如果两个线段相交，则-1。
特例：
队友指出的特例，还发了个表情给我
这种情况下，ans则等于原来的ans+2，

关于判断两个线段相交，截取一段林厚从的计算几何讲义：

用叉积去做，分两步：

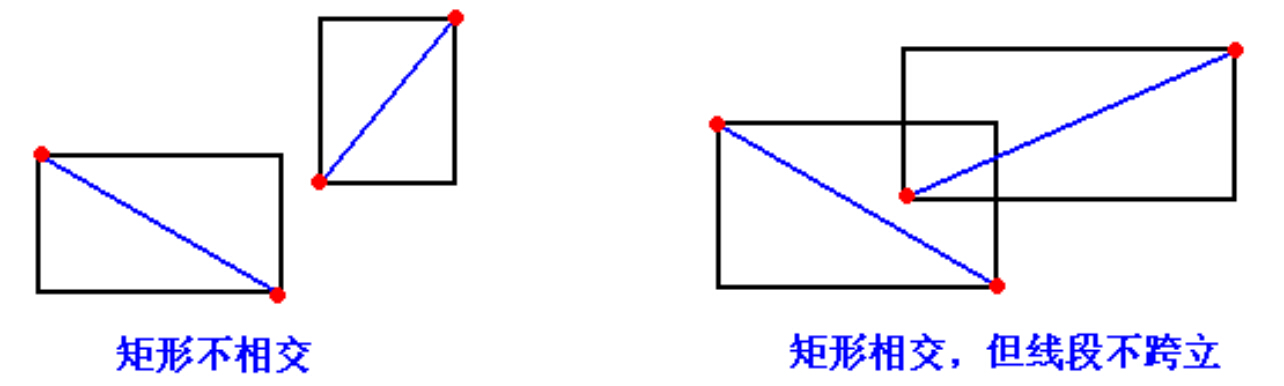
第 1 步：快速排斥试验，如果分别以 P1P2 ， P3P4 为对角线做矩形，而这两个矩形不相交，则
这两条线段肯定不相交，如下左图；即使两个矩形相交，这两条线段也不一定相交，如下右图，
这时再用第 2 步判断；

表示成语句，即两个矩形相交当且仅当下列式子为真：
（ max(x1,x2) ≥ min(x3,x4) ）∧ (max(x3,x4) ≥ min(x1,x2)) ∧（ max(y1,y2) ≥ min(y3,y4) ）∧(max(y3,y4) ≥min(y1,y2))
两个矩形相交必须在两个方向上都相交，式子的前半部分判断在 x 方向上是否相交，后半部
分判断在 y 方向上是否相交。

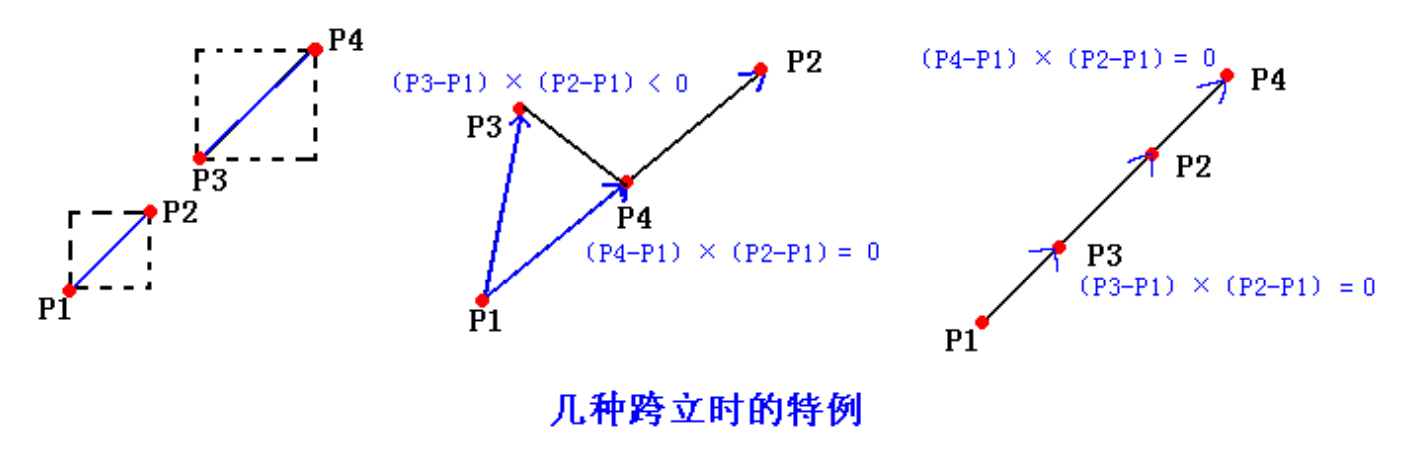
第 2 步：确定每条线段是否“跨立”另一条线段所在的直线。
跨立：如果点 P1 处于直线 P3P4 的一边，而 P2 处于该直线的另一边，则我们说线段 p1 p2 跨
立直线 P3P4，如果 P1 或 P2 在直线 P3P4 上，也算跨立。
两条线段相交当且仅当它们能够通过第 1 步的快速排斥试验，并且每一条线段都跨立另一条
线段所在的直线。

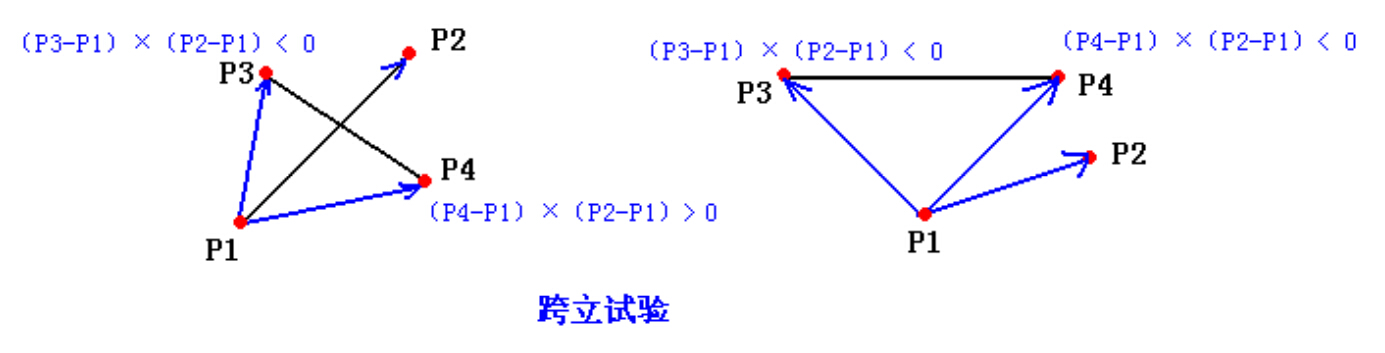
具体第 2 步的实现，只要用叉积去做就可以了，即只要判断矢量 p1 p3 和 p1 p4 是否在 p1 p2
的两边相对的位置上，如果这样，则线段 p1 p2 跨立直线 P3P4。
也即检查叉积（ P3-P1）×（ P2-P1）与（ P4-P1）×（ P2-P1）的符号是否相同，相同则不跨立，线段也就不相交，否则相交。
当然也有一些特殊情况需要处理，如任何一个叉积为 0，则 P3 或 P4 在直线 P1P2 上，又因为
通过了快速排斥试验，所以下图左边的情况是不可能出现的，只会出现右边的两种情况。
当然，还会出现一条或两条线段的长度为 0，如果两条线段的长度都是 0，则只要通过快速排斥试验就能确定；如果仅有一条线段的长度为 0，如 p3 p4 的长度为 0，则线段相交当且仅当叉积（ P3-P1）×（ P2-P1）。

over

在本题中，判断相交的代码很好写，死套公式即可
对于3个跨立时的特例：
第一个：在矩形判断的时候就排除了，不用管
第二个：如果是斜的，依然有解，按一般情况判断
如果是横的或者竖的，则无解，这里要写几个if
（见代码中注释：跨立特判2）
第三个：和第二个一样，斜的不管，横的或竖的无解（跨立特判3）
还有一个fuck判断，就是队友指出的特例，这里输出ans+2
fuck

所以差不多了，，，贴代码？
代码十分恶心，密集恐惧症患者请备好速效救心丸。
几个点的坐标好烦，好多判断条件好烦，if特别多

【code】

#include<cstdio>
#include<iostream>
#include<cmath>
#include<algorithm>
using namespace std;
int T,n,i,j,x[5],y[5],A,ans;
int X1,X2,X3,X4,Y1,Y2,Y3,Y4;
char c[5],ch;
bool ok;
bool fuck(){//fuck就是之前那张带表情的特例 
    if (X1==X2&&X1==X3&&X1==X4){
        if ((Y1>min(Y3,Y4)&&(Y1<max(Y3,Y4)))&&(Y2>min(Y3,Y4)&&(Y2<max(Y3,Y4))))return true;
        if ((Y3>min(Y1,Y2)&&(Y3<max(Y1,Y2)))&&(Y4>min(Y1,Y2)&&(Y4<max(Y1,Y2))))return true;     
    }
    if (Y1==Y2&&Y1==Y3&&Y1==Y4){
        if ((X1>min(X3,X4)&&(X1<max(X3,X4)))&&(X2>min(X3,X4)&&(X2<max(X3,X4))))return true;
        if ((X3>min(X1,X2)&&(X3<max(X1,X2)))&&(X4>min(X1,X2)&&(X4<max(X1,X2))))return true;
    }
    return false;
}

bool kl(int x1,int y1,int x2,int y2,int x3,int y3){             //跨立
    int xy1=x1*y2-x2*y1;
    int xy2=x1*y3-x3*y1;
    return xy1*xy2<0;
}

bool xj(){//xj，显然就是相交的开头 
    if (X1==X2&&X1==X3&&X1==X4&&min(Y1,Y2)<Y3&&Y3<=max(Y1,Y2)&&  //跨立特判3 
        (Y4>max(Y1,Y2)||Y4<min(Y1,Y2))) {return true;}
    if (Y1==Y2&&Y1==Y3&&Y1==Y4&&min(X1,X2)<X3&&X3<=max(X1,X2)&&
        (X4>max(X1,X2)||X4<min(X1,X2))) {return true;}

    if ((X1==X2)&&(X1==X3)&&(X1!=X4)&&(Y3<max(Y1,Y2))&&(Y3>min(Y1,Y2)))return true;//跨立特判2 
    if ((X1==X2)&&(X1==X4)&&(X1!=X3)&&(Y4<max(Y1,Y2))&&(Y4>min(Y1,Y2)))return true;
    if ((X3==X4)&&(X3==X1)&&(X3!=X2)&&(Y1<max(Y3,Y4))&&(Y1>min(Y3,Y4)))return true;
    if ((X3==X4)&&(X3==X2)&&(X3!=X1)&&(Y2<max(Y3,Y4))&&(Y2>min(Y3,Y4)))return true;
    if ((Y1==Y2)&&(Y1==Y3)&&(Y1!=Y4)&&(X3<max(X1,X2))&&(X3>min(X1,X2)))return true;
    if ((Y1==Y2)&&(Y1==Y4)&&(Y1!=Y3)&&(X4<max(X1,X2))&&(X4>min(X1,X2)))return true;
    if ((Y3==Y4)&&(Y3==Y1)&&(Y3!=Y2)&&(X1<max(X3,X4))&&(X1>min(X3,X4)))return true;
    if ((Y3==Y4)&&(Y3==Y2)&&(Y3!=Y1)&&(X2<max(X3,X4))&&(X2>min(X3,X4)))return true;

    if (max(X1,X2)<=min(X3,X4)) {return false;}                  //矩形相交 
    if (max(X3,X4)<=min(X1,X2)) {return false;}  
    if (max(Y1,Y2)<=min(Y3,Y4)) {return false;}  
    if (max(Y3,Y4)<=min(Y1,Y2)) {return false;}  
    if (!kl(X2-X1,Y2-Y1,X3-X1,Y3-Y1,X4-X1,Y4-Y1)) {return false;}  //跨立实验 
    if (!kl(X4-X3,Y4-Y3,X1-X3,Y1-Y3,X2-X3,Y2-Y3)) {return false;}  
    if (!kl(X3-X4,Y3-Y4,X1-X4,Y1-Y4,X2-X4,Y2-Y4)) {return false;}  
    if (!kl(X1-X2,Y1-Y2,X3-X2,Y3-Y2,X4-X2,Y4-Y2)) {return false;}  
    return true;
}

int main (){
    freopen("fuck.in","r",stdin);
    scanf("%d",&T);
    while (T--){
        scanf("%d%C",&n,&ch);
        A=0;
        for (i=1;i<=n;i++)
          for (j=1;j<=n;j++){
              cin>>ch;
              if (ch=='.')continue;
              x[++A]=i;y[A]=j;c[A]=ch;
              //printf("%d %d %c
",i,j,ch);
          }
        //for (i=1;i<=4;i++)printf("%d %d %d %c
",i,x[i],y[i],c[i]);
        ok=false;//这个取点感觉写的好挫，不过我还没想到更好的处理方案，先这么写吧
        for (i=1;i<4&&!ok;i++) for (j=i+1;j<=4&&!ok;j++)
          if ((c[i]=='1')&&(c[j]=='1'))
          {X1=x[i];Y1=y[i];X2=x[j];Y2=y[j];ok=true;break;}
        ok=false;
        for (i=1;i<4&&!ok;i++) for (j=i+1;j<=4&&!ok;j++)
          if ((c[i]=='2')&&(c[j]=='2'))
          {X3=x[i];Y3=y[i];X4=x[j];Y4=y[j];ok=true;break;}
        ans=abs(X1-X2)+abs(Y1-Y2)+abs(X3-X4)+abs(Y3-Y4)+2;
        //printf("%d %d %d %d
%d %d %d %d
",X1,Y1,X2,Y2,X3,Y3,X4,Y4);

        if (xj())printf("-1
");
        else if (fuck())printf("%d
",ans+2);
        else printf("%d
",ans);
    }
    return 0;
} 

PS：本题似乎也可以用爆搜过掉（clairs爷就是这么干的），做两次bfs。
不过clairs爷说这套题有毒，，，= =
自己第一天写残了，第二天准备重写爆搜的时候复制第一天读入发现问题了（就是代码里感觉写的挫的一段），瞬间爆炸。。。