UVA1658海军上将，拆点费用流

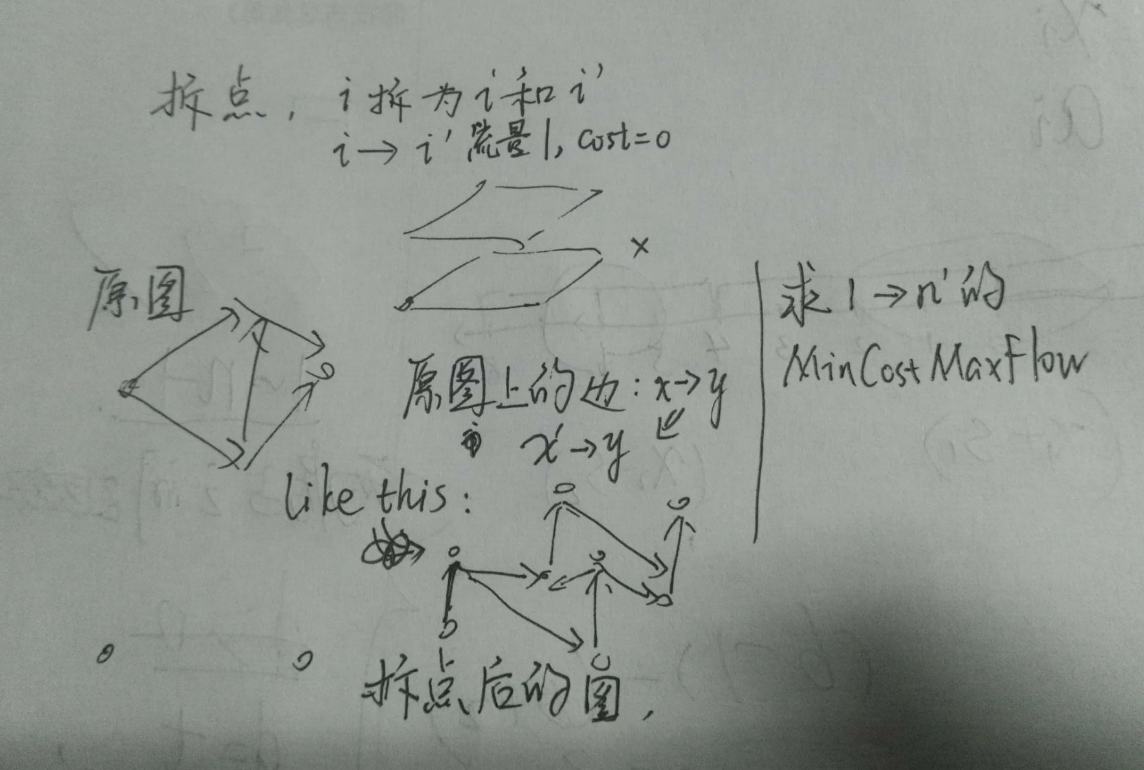
刘汝佳紫书上的题
题意：给n个点m条边的有向加权图，求1->n的两条不重复的路径，使sum权最小
（不重复的路径是指，两条路径没有公共点）

思路见图

用的紫书371页的模板

#include<queue>
#include<cstdio>
#include<vector>
#include<cstring>
#include<iostream>
#include<algorithm>
using namespace std;
typedef long long LL;
const int N = 20007;
const int INF=0x3f3f3f3f;
struct MCMF{
    struct Edge{
        int from,to,cap,flow,cost;
        Edge(int x,int y,int z,int u,int v){
            from=x;to=y;cap=z;flow=u;cost=v;
        }
    };
    vector <Edge> edges;
    vector <int > G[N];
    int n,m,inq[N],d[N],p[N],a[N];

    inline void Init(int n){
        this->n = n;
        edges.clear();
        for (int i=1;i<=n;i++)G[i].clear();
    }
    inline void AddEdge(int f,int t,int c,int w){
        edges.push_back(Edge(f,t,c,0, w));
        edges.push_back(Edge(t,f,0,0,-w));
        int top = edges.size();
        G[f].push_back(top-2);
        G[t].push_back(top-1);
    }

    bool spfa(int s,int t,int flow,LL &cost){
        for (int i=0;i<=n;i++)d[i]=INF;
        memset(inq,0,sizeof(inq));
        d[s]=0;inq[s]=1;p[s]=0;a[s]=INF;
        queue<int>Q;Q.push(s);
        for (;!Q.empty();){
            int u =Q.front();Q.pop();inq[u]=0;
            for (int i=0;i<G[u].size();i++){
                Edge &e = edges[G[u][i]];
                if (e.cap<=e.flow||d[e.to]<=d[u]+e.cost)continue;
                d[e.to] = d[u] + e.cost;
                p[e.to] = G[u][i];
                a[e.to] = min(a[u],e.cap-e.flow);
                if (!inq[e.to]){Q.push(e.to);inq[e.to]=1;}
            }
        }
        if (d[t]==INF)return 0;//false
        flow += a[t];
        cost +=(LL)d[t]*(LL)a[t];
        for (int u=t;u!=s;u=edges[p[u]].from){
            edges[p[u]  ].flow += a[t];
            edges[p[u]^1].flow -= a[t];
        }
        return 1;//true
    }

    //需要保证初始网络中没有负权
    int mcmf(int s,int t,LL &cost){
        int flow =0; cost = 0;
        for (;spfa(s,t,flow,cost););
        return flow;
    }//MinCostMaxFlow
}g;

int main(){
    //freopen("in.txt","r",stdin);
    int x,y,z,n,m;
    for (LL ans;~scanf("%d%d",&n,&m);){
        g.Init(n<<1);//begin build gragh
        for (int i=1;i<=n;i++){
            if(i==1||i==n)g.AddEdge(i,i+n,2,0);
            else g.AddEdge(i,i+n,1,0);
        }
        for (;m--;){
            scanf("%d%d%d",&x,&y,&z);
            g.AddEdge(x+n,y,1,z);
        }   //end Build gragh
        int flow = g.mcmf(1,n<<1,ans);
        printf("%lld
",ans);
    }
    return 0;
}