从中序后序遍历构造

1.构造二叉树的必要条件
必须需要中序遍历和一个前序或者中序遍历
构造二叉树=前序+中序 =后序+中序
2.那如何根据中序和后序遍历去构造二叉树呢？
比如给出 inorder(中序)=[9,3,15,27]
postorder(后序遍历)=[9,15,7,20,3]
就可以构造出一个唯一的二叉树：

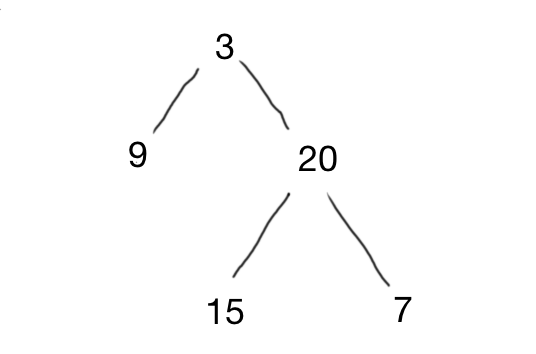
那怎么做呢？采取分割法。
以后序数组的最后一个元素作为分割点，你可以把它理解为当前树的中点，然后切开中
序数组，划分成左右子树，直到后序数组只有一个元素

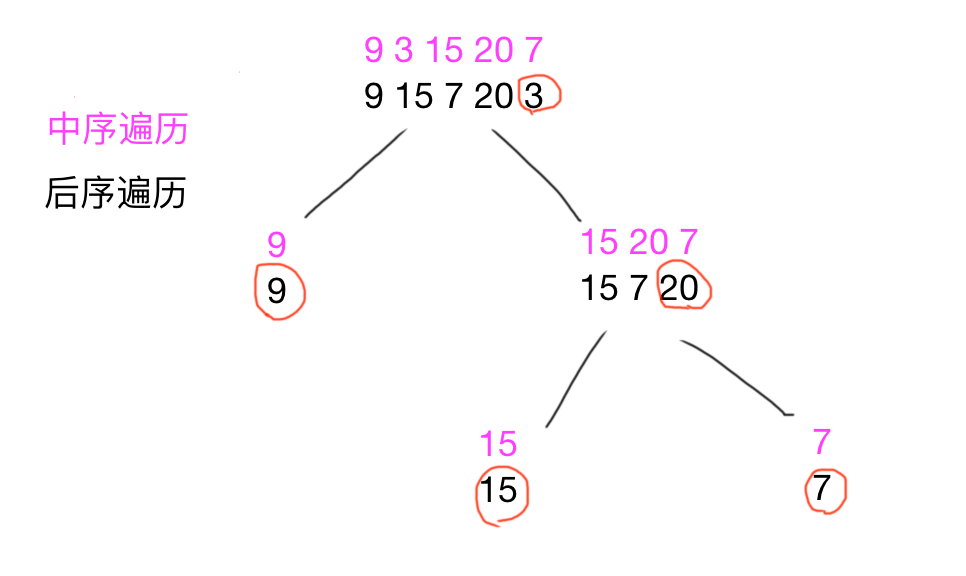
使用递归算法处理

TreeNode* build(vector<int>&inorder,vector<int>&postorder)
    {
        1.如果后序遍历为空，那么这是一个空树
        if(postorder.size()==0)return nullptr;
        2.选择后序遍历的最后一个元素最为分割点
        int rootVal=postorder[postorder.size()-1];
        TreeNode * root=new TreeNode(rootVal);
        3.如果这个时候后序数组只有1个元素，那么它是叶子节点
        if(postorder.size()==1)return root;
        4.在中序遍历的数组内部寻找割点
        int dimpoint;
        for(dimpoint=0;dimpoint<inorder.size();dimpoint++)
        {
            if(inorder[dimpoint]==rootVal){break;}
        }
        切割中序左数组,使用左闭右开原则
        vector<int> leftinorder(inorder.begin(),inorder.begin()+dimpoint);
        切割中序右数组
        vector<int> rightinorder(inorder.begin()+dimpoint+1,inorder.end());
        切割后序数组为左右数组
        postorder.resize(postorder.size()-1);
        vector<int> leftpostorder(postorder.begin(),postorder.begin()+leftinorder.size());;
        vector<int> rightpostorder(postorder.begin()+leftinorder.size(),postorder.end());
        
        root->left=build(leftinorder,leftpostorder);
        root->right=build(rightinorder,rightpostorder);
        return root;
    }

但是，前序和中序无法唯一的确定一颗二叉树。