iOS.Animation.Math-behind-CATransform3D

iOS CoreAnimation: Math behind CATransform3D

1. What's CATransform?

Matrix Transform: 

"User space = your view (points)

Device space = hardware device native resolution (pixels)

On print or display, Quartz maps user space coordinates to device space coordinates" Ref[2]

CATransform用来控制这个映射过程(User Space => Device Space)。

CATransform3D的定义:

struct CATransform3D
{
  CGFloat m11, m12, m13, m14;  // row 1 of matrix
  CGFloat m21, m22, m23, m24;  // row 2 of matrix
  CGFloat m31, m32, m33, m34;  // row 3 of matrix
  CGFloat m41, m42, m43, m44;  // row 4 of matrix
};

点P(x, y, z, w)经过平移变换(Translate Transform)后:

(x, y, z, 1) * 1  0  0  0
               0  1  0  0  = (x+tx, y+ty, z+tz, 1)
               0  0  1  0
               tx ty tz 1

点P(x, y, z, w)经过矩阵T进行变换后为点P₁(x₁, y₁, z₁, w₁):

(x, y, z, 1) * m11  m12  m13  m14      m11*x+m21*y+m31*z+m41   // x1
               m21  m22  m23  m24  =   m12*x+m22*y+m32*z+m42   // y1
               m31  m32  m33  m34      m13*x+m23*y+m33*z+m43   // z1
               m41  m42  m43  m44      m14*x+m24*y+m34*z+m44   // w1

2. Using m34

尤其是那个神奇的m34。

(1, 1, 1, 1) * 1  0  0  0
               0  1  0  0 
               0  0  1 -1/500 = (1, 1, 1, 1*(-1/500)+1) = (1, 1, 1, 499/500) = (500/499, 500/499, 500/499, 1) 
               0  0  0  1

通过以上Matrix变换, 点P(1,1,1)的坐标变化为P₁(500/499, 500/499, 500/499); 点Q(1,1,-1)的坐标变化为Q₁(500/501, 500/501, -500/501, 1)。选取P和Q两个点为例，可见经过设置m34值的Matrix进行变换后呈现3D Perspective(透视)效果。

3. Coordinate Systems

"OpenGL adopts the Right-Hand Coordinate System (RHS). In the RHS, the x-axis is pointing right, y-axis is pointing up,

and z-axis is pointing out of the screen. " Ref[6]

"RHS is counter-clockwise (CCW). The 3D Cartesian Coordinates is a RHS.

Some graphics software (such as Microsoft Direct3D) use Left-hand System (LHS), where the z-axis is inverted.

LHS is clockwise (CW). " Ref[6]

3.1 Core Animation is LHCS or RHCS?

根据Ref[4], Ref[5]中的内容，Core Animation(iOS Platform)使用左手坐标系(Left-Hand Coordinate System/LHCS): 

"Core Animation uses a left-handed coordinate system with the Z-axis’ positive space extending from the screen towards the viewer." Ref[5] 

"iOS中使用的左手坐标系，其原点在左上角。" Ref[4]

注：目前尚未找到官方文档来说明Core Animation使用LHCS。

3.2 What's LHCS?

如图Figure-1(图片来源: http://flylib.com/books/en/2.416.1.16/1/)所示，拇指指向Y轴的正方向，食指指向Z轴的正方向，中指指向X轴的正方向。

  

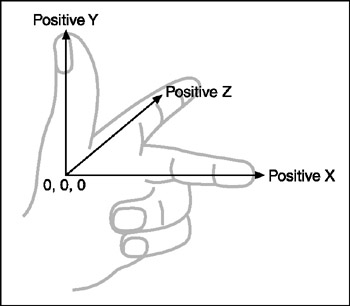
图Figure-2是右手坐标系示例图(图片来源: http://flylib.com/books/en/2.416.1.16/1/)

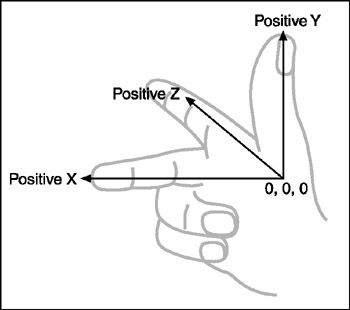
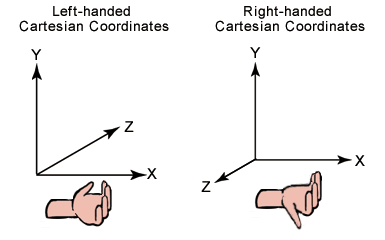
Figure-3:左手笛卡尔坐标系和右手笛卡尔坐标系对比

图片来源: https://sites.google.com/site/craigandera/craigs-stuff/directx-home/managed-direct3d-tutorial/06-coordinate-systems-and-transforms

左手笛卡尔坐标系：左手拇指与手臂垂直，其它手指也与手臂垂直。拇指指向Z轴正方向，手臂指向X轴正方向，其它手指指向Y轴正方向。

iOS Core Animation Left-Hand Cartesian Coordinates (LHCC)

图Figure-1是标准的LHCS，而iOS平台上Core Animation中CALayer的Y轴正方向是向下的，那么iOS平台上Core Animation的坐标系变为(下图，Figure-4):

 

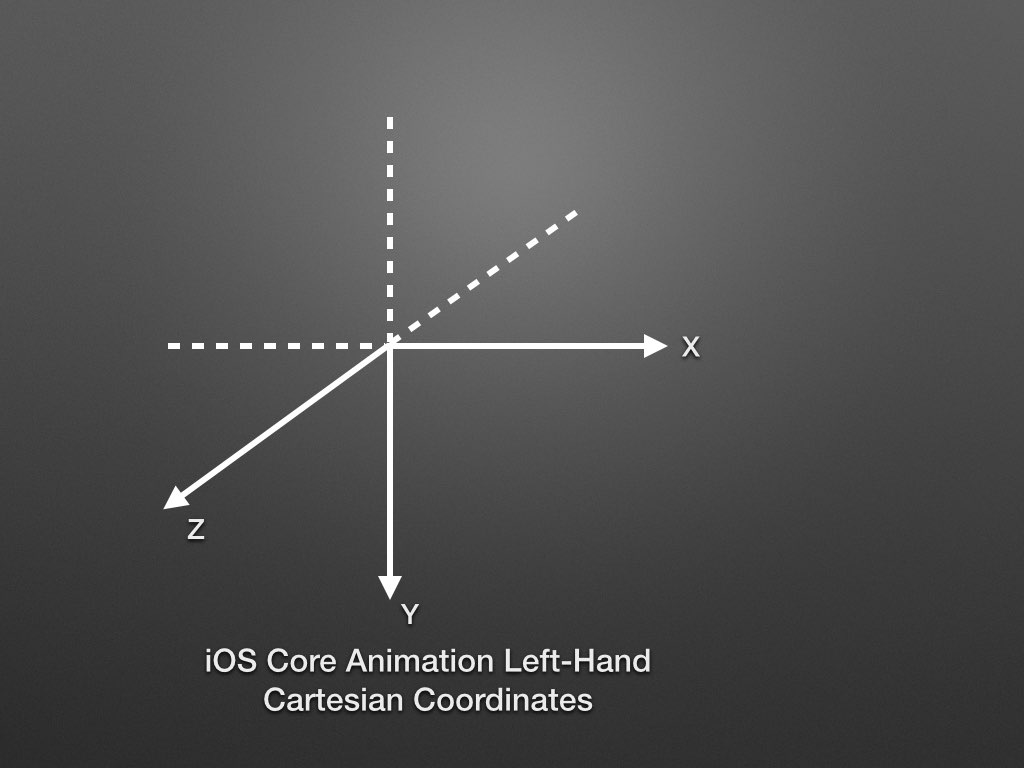
3.3 Positive Rotation 

Positive Rotation: 正向旋转

"Positive rotation is clockwise about the axis of rotation." Ref[8] 

对于LHCC而言，(从旋转轴的正方向看)沿旋转轴的顺时针旋转是正向旋转。例如图Figure-5所示，旋转轴是Z轴，从Z轴正方向往Z轴方向

看去，顺时针的旋转是正向旋转:

 

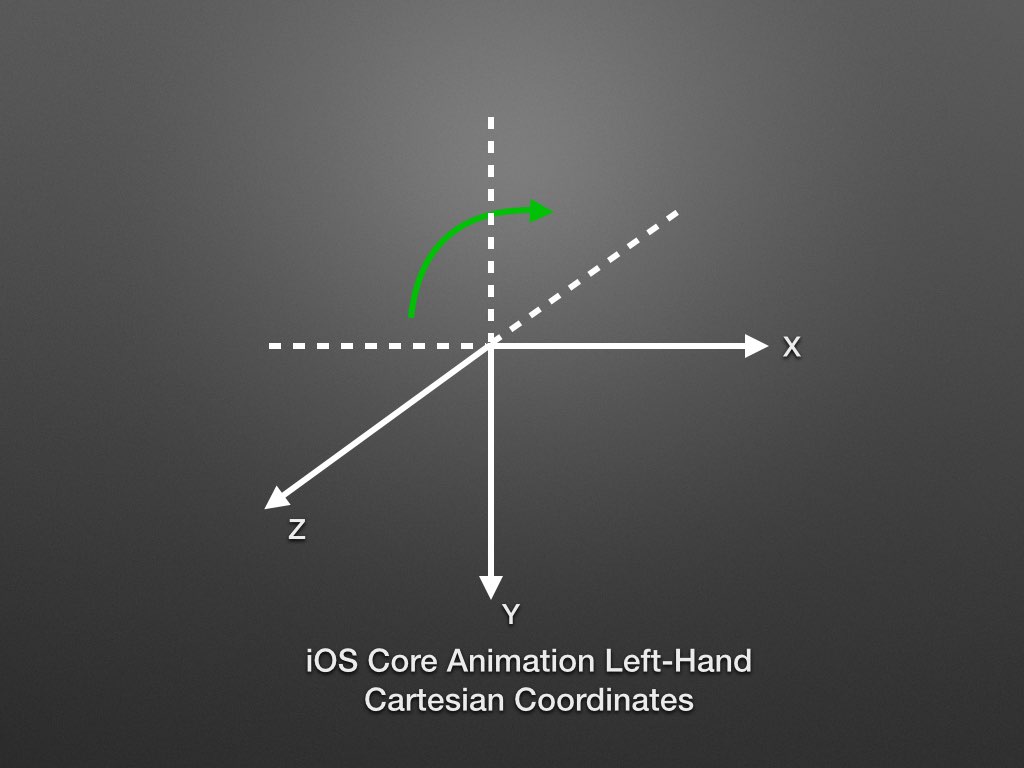
左手握住Z轴，拇指指向Z轴正方向，其它手指指向的方向即LHCC中的Positive Rotation。

3.4 Demo for Rotation

---

Reference

1. UIView+Fold.m

AnimationDemo 中对m34的使用。

Created by Rachel Bobbins on 1/31/15.

2. Enter the Matrix (AAAA)

http://cocoaconf.com/slides/chicago-2012/matrix.pdf

github.com/mpospese/EnterTheMatrix (TO Debug)

3. iOS.Math-in-CGAffineTransform 

Math behind the CGAffineTransform 

4. Mac，iOS界面中的三维坐标系

http://geeklu.com/2012/06/3d-coordinate-system/

5. CA's 3D Model 

2D planes in a 3D world, simples.

https://milen.me/writings/core-animation-3d-model/

6. 3D Graphics with OpenGL

Basic Theory

https://www.ntu.edu.sg/home/ehchua/programming/opengl/CG_BasicsTheory.html#zz-4.1

7. iOS Core Animation: Advanced Techniques, Part 1: The Layer Beneath  (TO Read)

https://gist.github.com/JeOam/94e833bcefd738d805cc

8. Left- vs. Right-handed coordinate systems

https://www.evl.uic.edu/ralph/508S98/coordinates.html

Positive rotation