画图从直觉上来讲就是为了更加清晰的展示时序数据所呈现的规律(包括趋势,随时间变化的规律(一周、一个月、一年等等)和周期性规律),对于进一步选择时序分析模型至关重要。下面主要是基于pandas库总结一下都有哪些常见图可以用来分析。总共有下面几种:
- 线形图
- 直方图和密度图
- 箱形图
- 热力图
- 滞后图
- 散点图
- 自相关图
(1)线形图
这是最基本的图了,横轴是时间,纵轴是变量,描述了变量随着时间的变化关系,图中显然也容易发现上述的潜在规律。直接上代码:
# -*- coding: utf-8 -*- from pandas import Series import matplotlib.pyplot as plt data = Series.from_csv('minimum.csv',header=0) data.astype(float) print(data.head()) data.plot(style='r.') plt.show()
也可以只看其中一年的,比方说1990年,如下:
data = Series.from_csv('minimum.csv', header=0) one_year = data['1990'] one_year.plot()
这个解决的一个问题是object类型是不能plot的,查看pandas 读csv文件 TypeError: Empty 'DataFrame': no numeric data to plot
另外plot的style可以查看文档自己选择喜欢的,文档链接
(2)直方图和密度图
直方图,大家是知道的,他没有时序,只是在一个时间范围的变量范围统计,比方说这些数据分成10个bins,我们会看到每个bin的数量(比方说多少天,月等等),这种统计方法同密度图是一样的,能看到变量在哪些取值范围比较多,哪些比较少等等,观测到数据的潜在分布规律。
from pandas import Series import matplotlib.pyplot as plt data = Series.from_csv('minimum.csv', header=0) data.hist() plt.show() data.plot(kind='kde') plt.show()
这里面主要有一个问题,就是什么是kde:Kernel Density Estimation,sklearn的tutorial会告诉你,请看文档
(3)箱形图
from pandas import * import matplotlib.pyplot as plt data = Series.from_csv('minimum.csv', header=0) groups = data.groupby(TimeGrouper('A')) years = DataFrame() for name,group in groups: years[name.year]=group.values years.boxplot() plt.show()
这里贴一下图:
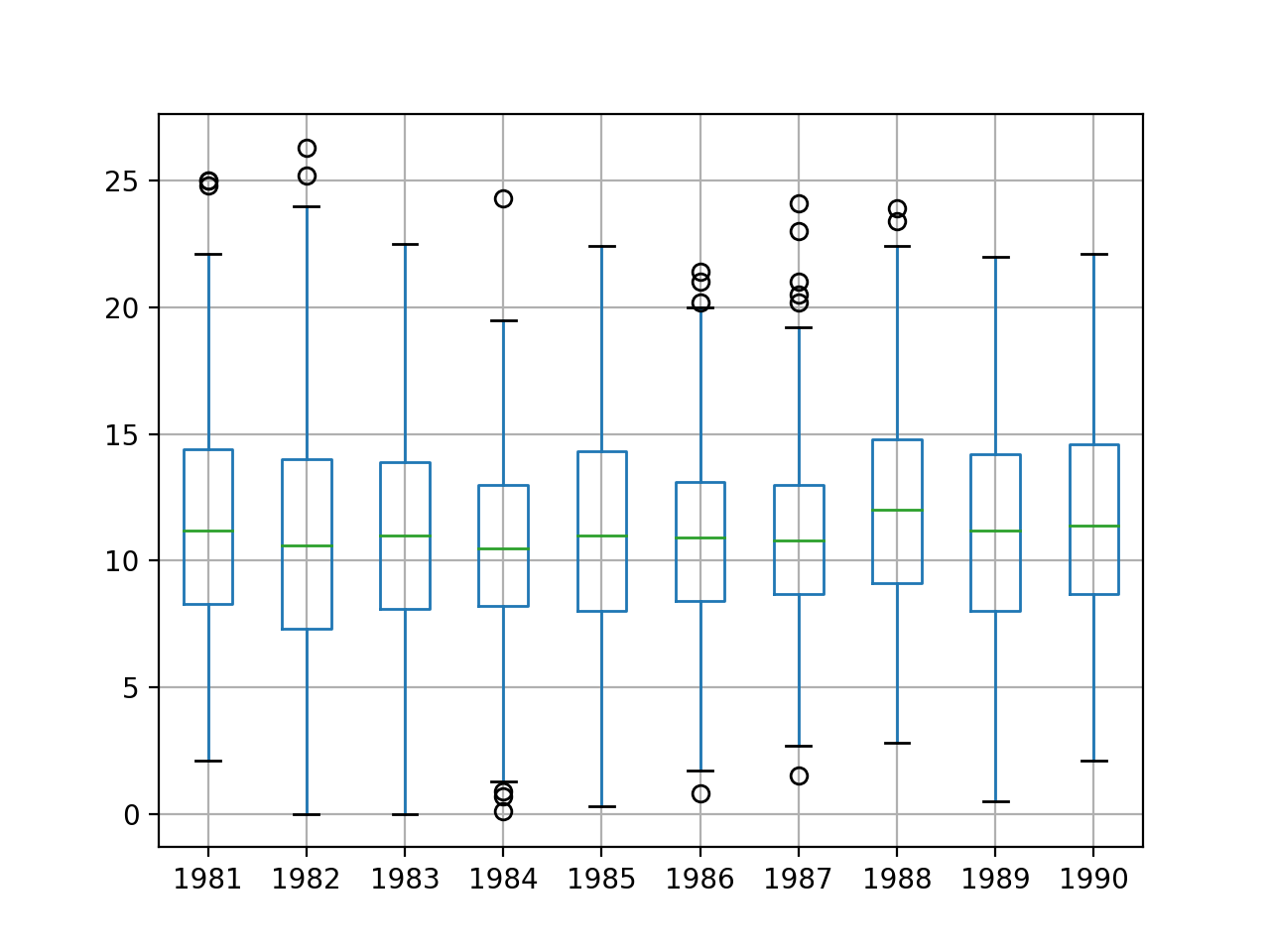
顺便介绍一下箱形图,它能显示出一组数据的最大值、最小值、中位数、及上下四分位数,其中最主要的是最大值最小值给的是在上下四分位数的某个区间里面,形成一个盒子加上胡须(因此也叫盒须图),例如上图1981年,最大值是20-25之间,最小值在0-5之间,务必记住是在一个大概率区间里面最大最小,不是实际的最大最小,离开了这个区间会有很多小圆圈和*表示,圆圈表示离群值,*表示极端值。
当然也可以取出其中一年分析一下:
from pandas import * import matplotlib.pyplot as plt data = Series.from_csv('minimum.csv', header=0) data = data['1990'] groups = data.groupby(TimeGrouper('M')) months = concat([DataFrame(x[1].values) for x in groups], axis=1) months = DataFrame(months) months.columns = range(1,13) months.boxplot() plt.show()
(4)热力图
热力图就更加形象点了,虽然我们不知道数值,但是通过颜色我们能看看极值的分布,颜色越鲜艳,数值越大(红黄),颜色越暗淡,数值越小(蓝绿),当然显示也有可能不一样。
#1988年的例子 from pandas import * import matplotlib.pyplot as plt data = Series.from_csv('minimum.csv', header=0) data = data['1988'] groups = data.groupby(TimeGrouper('M')) months = concat([DataFrame(x[1].values) for x in groups], axis=1) months = DataFrame(months) months.columns = range(1,13) plt.matshow(months,interpolation=None,aspect='auto') plt.show()
(5)滞后图和散点图
这里应该注意一下,滞后图与散点图可以按照时序画,那就是(1)里面的线形图了,这里讲的其实不是时序的,而是分析数据相关性的,我们给数据一段时间的观测间隔,因为假定前面的数据和后面的数据有关系,是正相关或是负相关还是什么,选定一个间隔,plot一下。
from pandas import * import matplotlib.pyplot as plt from pandas.plotting import lag_plot data = Series.from_csv('minimum.csv', header=0) lag_plot(data) plt.show()
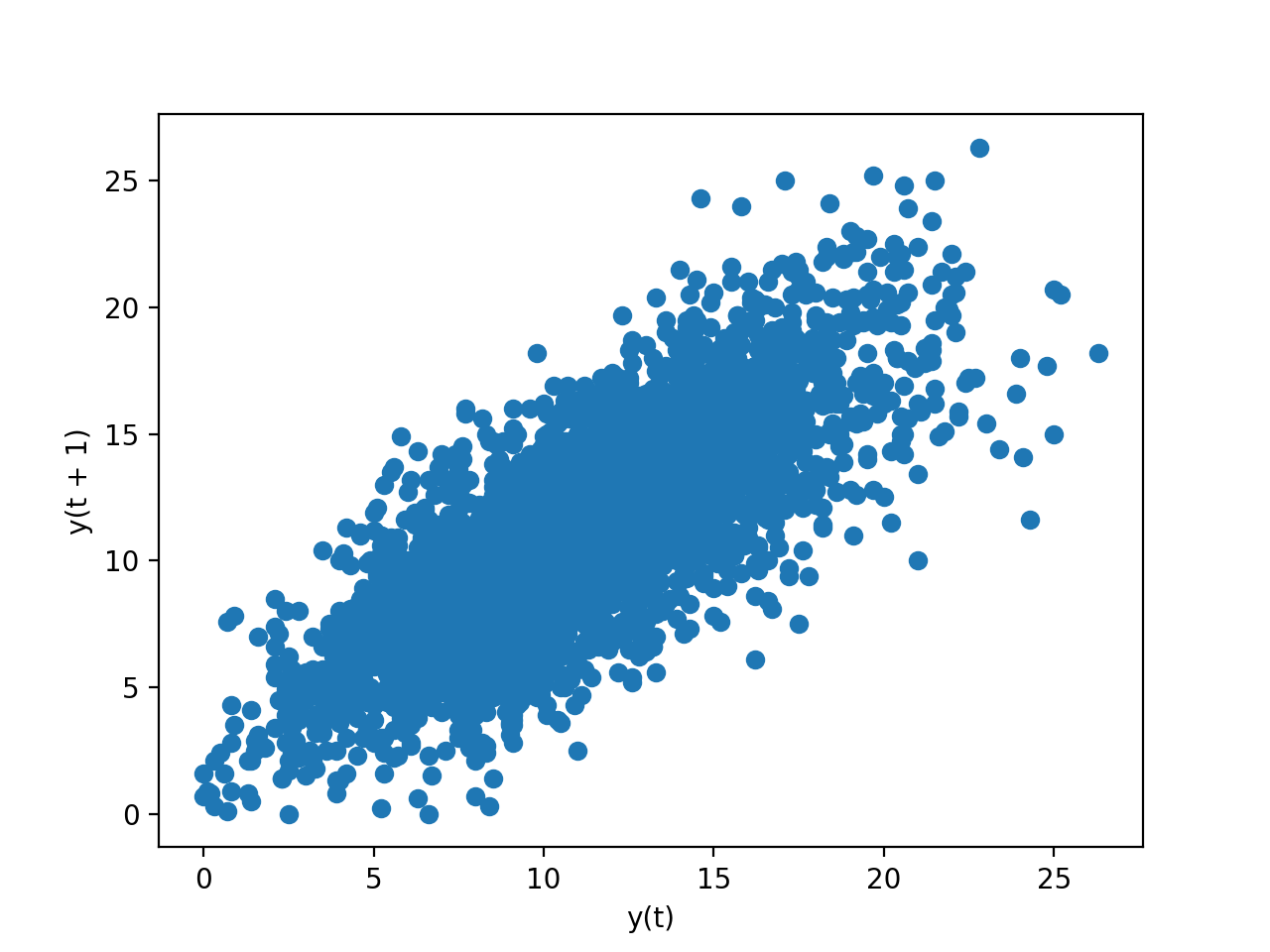
明显我们看到了正相关。下面给出一个星期的散点图,我们可以看到间隔一天、两天、三天......
from pandas import * import matplotlib.pyplot as plt data = Series.from_csv('minimum.csv', header=0) values = DataFrame(data.values) lags = 7 columns = [values] for i in range(1,(lags + 1)): columns.append(values.shift(i)) dataframe = concat(columns, axis=1) columns = ['t'] for i in range(1,(lags + 1)): columns.append('t-' + str(i)) dataframe.columns = columns plt.figure(1) for i in range(1,(lags + 1)): ax = plt.subplot(240 + i) ax.set_title('t vs t-' + str(i)) plt.scatter(x=dataframe['t'].values, y=dataframe['t-'+str(i)].values) plt.show()
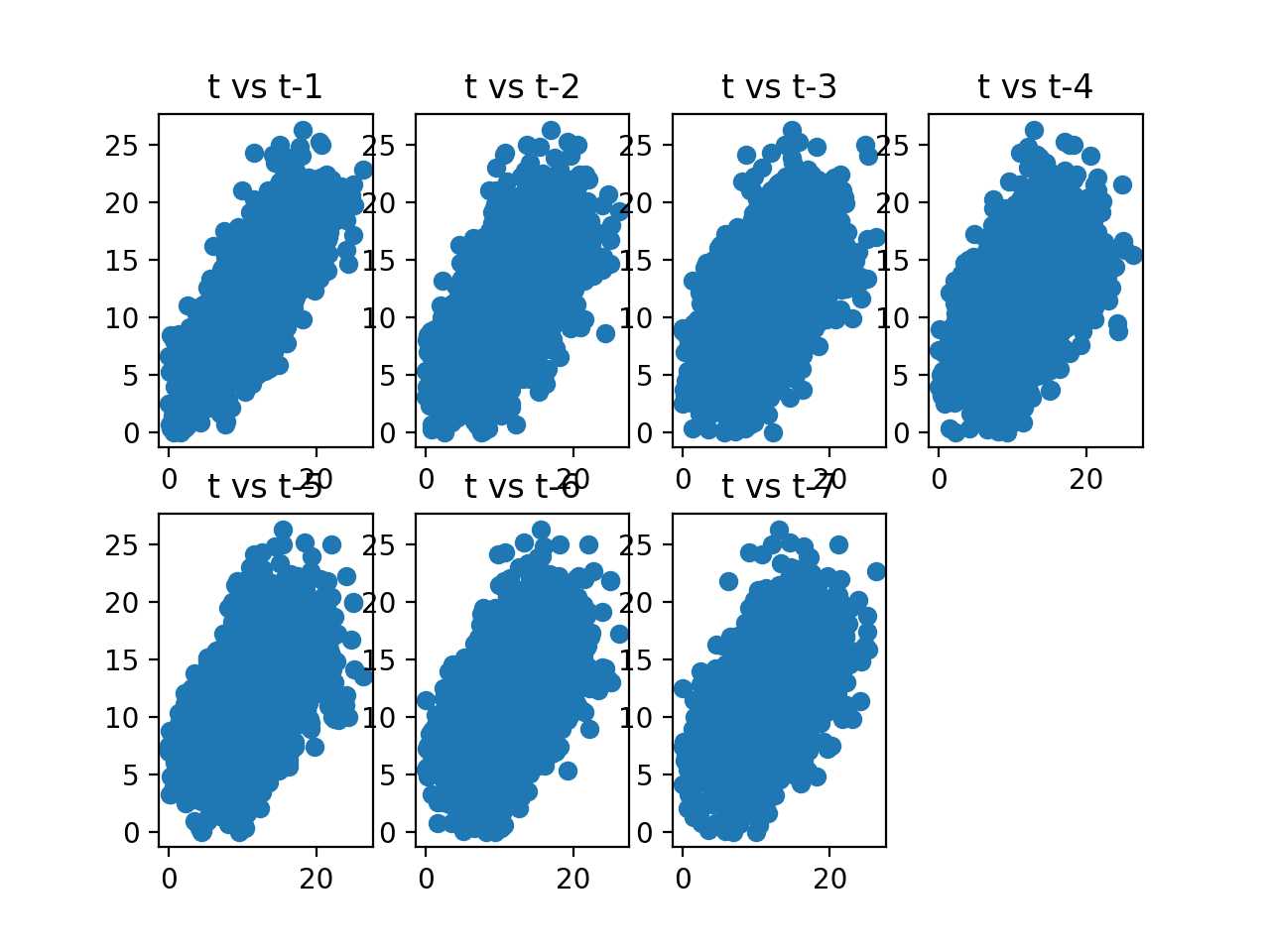
(6)自相关图
这个不用说的,其实就是考虑数据和一定间隔数据的相关性,越接近1是正相关,接近-1是负相关,接近0就是相关性很低。下面就是计算公式(右边是左边的特殊情形,也就是自相关图的公式,因为是自己和自己所有可能的间隔产生的),下面代码给的自相关默认是数据和滞后1步的相关性。
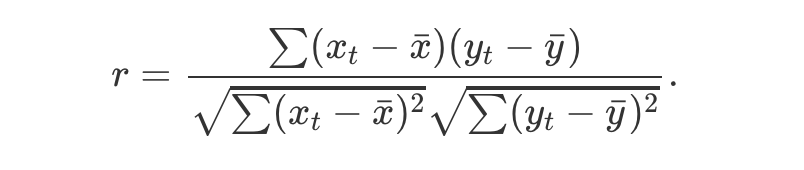
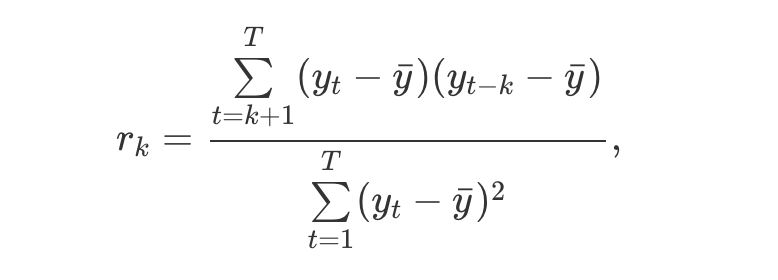
from pandas import Series import matplotlib.pyplot as plt from pandas.plotting import autocorrelation_plot series = Series.from_csv('minimum.csv', header=0) autocorrelation_plot(series) plt.show()
当然,这些并没有介绍完全,详细版还是附在下面: