初中数学教学中的几何画板
转载 https://zhuanlan.zhihu.com/p/101135423
一些经验很不错，怕后面找不到，转载过来
不要满足于从小笼子换到大笼子里
取消关注
34 人赞同了该文章
一、几何画板教学的特点
在数学教学中，几何画板可以说是每一个数学教师的一样“法宝”，在教学中发挥了重要的作用。它相比于传统的“图片”“黑板绘图”有这样几个特点暨优点:
- 动态化。同样是教学中的演示法，几何画板与其它呈现的方式之不同就在于，它的作图前后会自动的保持几何关系（数量关系）不变。从而使得它可以动态的演示一些基本事实，直观的展现出在特定关系下产生的奇妙性质。
- 简单化。尤其体现在学生探究性学习中，几何画板快速作图（尤其是函数作图），它便捷的操作让课堂的整体效率提高，并让学生的精力尽可能的避免被分散。
- 可操作化。不仅教师可以演示，由于其操作的简单性，可以让学生主动、自主的进行一些操作，不仅可以加深印象，还可以让学生自行验证一些基本结论，便于探究性学习、合作学习的开展。
二、几何画板教学的误区与原则
但是，饶是几何画板如此好用，也不是万能的。这是由我们的教学目的所决定的。以初中几何为例，基本上是要求学生掌握“公理化”的方法，由逻辑演绎的解决问题。在“提出问题——给出假设——验证”的环节中，验证的方法应当是演绎的、逻辑的思想，而不是直观。
几何画板只能是初中教学的手段、过程中的一环，而不可以作为结果。从这个意义上来说，几乎所有的新授课上，几何画板都不能用来“解释”概念，只能让学生直观“认识”“体验”概念、基本事实。
结合它的特点与误区，我个人总结出这两条原则：
- 几何画板可以作为展示概念、事实、结论的手段，但是必须配有说理。例如：路径问题，可以给学生看路径的变化，但是必须阐明为什么会这样。
- 如果没有动态展示的必要，就不必刻意的使用几何画板插件（用几何画板作图不算使用几何画板教学）。例如：三角形内角和为180°，不需要用几何画板度量任意三角形的三个角。这是因为在中学我们采用平行线来证明了这个结论，小学才是使用这种归纳推理的方式，而且这个定理不需要动态的理解。
三、几何画板教学的实例
说了这么多我来演示几个几何画板教学的实例，我将课型简单的归为两类，一类是新授课，一类是习题课。
- 不等式（组）——习题课上的使用
例题1：关于x的不等式-3x+a≥0的正整数解只有1，2，3，4，求a 的取值范围.
不等式（组）这一章节看起来和“几何”画板实在没什么关系，因此在新授环节几乎用不到，但是对于一些相对复杂的、含有参量的、需要用到图示法的题目，可以用几何画板来演示。
不等式（组）——习题课上的使用
2.一次函数图象与系数的关系——新授课上的使用
函数图象其实是我认为最有在新授课使用几何画板进行教学价值的内容，以一次函数为例，我们知道k（斜率）只会影响一次函数图象的倾斜角度，b（截距）只会影响一次函数图象的位置（与y轴的交点）。但是在传统的教学中，我们往往会要求学生直接记忆下各种情况直线经过哪些象限，如下表：
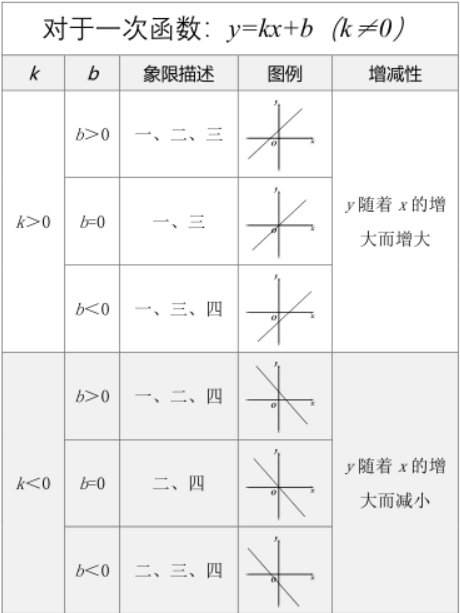图表 1一次函数系数与图象关系图
如果说死记硬背完全没有效果，那也实在不公道，但是效率低是肯定的，理解程度低也是肯定的。在这种教法下以后临界问题就不好理解，平行的一次函数图象k必然相等也会很难理解。我们看下用几何画板来演示。
一次函数图象与系数的关系
3.几何——习题课上的使用
实际上，我觉得在几何板块上，使用几何画板来新授某些概念是最无必要的，因为几何我们主要使用演绎推理的证明来解决问题，过于依赖几何画板没有好处。在概念学习阶段也少有需要动态理解的概念。但是，在几何习题中，却有很多学生难以理解的动态，所以用在习题课中反而较多。
例题2：如图，一根长为10米的竹竿AB斜靠在垂直于地面的墙上（∠O=90°），竹竿AB的倾斜角为α．当竹竿的顶端A下滑到点A′ 时，竹竿的另一端B向右滑到了点B′，此时倾斜角为β，则线段AA'的长为________米．当竹竿AB滑到A′B′位置时，AB的中点P滑到了A′B′的中点P′位置，则点P所经过的路线长为 __________米．（两空格均用含α、β的式子表示）
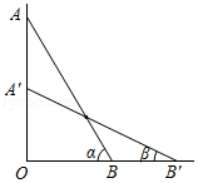
几何——习题课上的使用
可以看出第二空如果直接演示，学生虽然只看到一段弧线，也会知道多半是圆。但是在实际的考试之中，学生并不能使用几何画板，因此相比于“路径”是怎么样的，更重要的是该怎么样去想到如何探究路径。如果用几何画板给学生看一眼，然后直接给出答案，那么就本末倒置，这几何画板不如不用。
四、总结与反思
总的来说，个人的心得体会就只有那么多，没什么深刻的内涵，可谓是一览无遗了。但文章最后，总归要强行升华一下主题的。
其一，信息技术的发展带动了教学技术的进步，其实不仅仅是几何画板，比如现代计算机教学的普及，在新授函数的概念的时候，很多时候可以使用excel作为课程素材来使用，让学生直接体验到函数的用处。不管什么时候，教师都应该主动去探索新的技术，新的手段。但是一定要记得，手段、方法都不是目的本身，一定要立足于教学目的才能不反为技术所困。
其二，是我对自己的一点批判，在路径问题处，我说考场上不能用“几何画板”，所以还是要有精细的说理。其实这不反而落实了“应试教育”吗？未来的数学教育是什么样的——我不觉得还会是这样。据我了解，在PISA测试中，已经将利用工具辅助解决数学问题的能力列入参考。相比于强大的推理能力，在现代可能是数学建模的能力更为重要，这很可能会是一种趋势。但靠自己想出“路径”和依靠计算机技术发现“路径”的人，到底谁更优秀，其实可能是时代所决定的。逻辑推理能力强的人和建模能力强的人，究竟哪种才是未来需要的人才，其实犹未可知（在笔者心里其实认为趋势在向建模能力发展，PISA这一全球化的测试明确在测试中显示了这种倾向）。只能说，“不可止步于演示，而要说理”的原则，预期是说我对教学目标的认识，不如说是对学生必然面临考试的妥协。但我坚持，如果你是一个理想主义的教师，你也不会演示一遍就万事大吉，你得能教会学生用这个软件，教会学生建模的思想。
总而言之，就是不要停止去思考，不要停止接受新的事物。在精进自己教学水平的同时，也要去思考教育本身的目的。
与诸位共勉。