In this lesson, you'll dive deeper into the intuition behind Logistic Regression and Neural Networks.
You'll also implement gradient descent and backpropagation in python right here in the classroom.
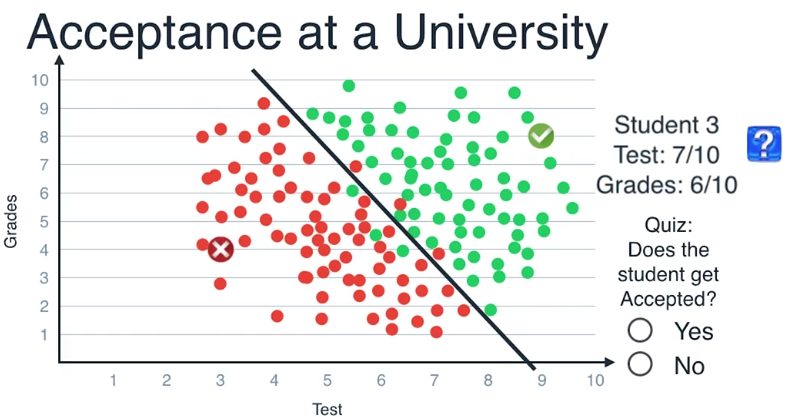
我们以这条线为模型,每当接到新的学生申请,我们把他们的成绩画在坐标图上
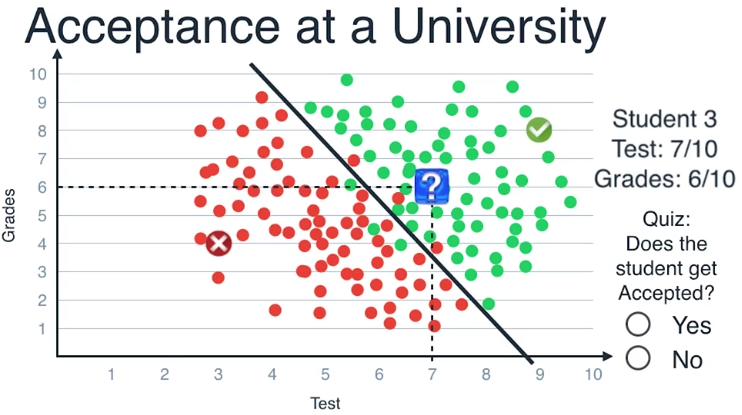
如果数据点是在这条线的上方,那么预测他们会被录取
如果数据点是在下方,则预测他们会被拒绝,学生的数据坐标为(7,6)
位于直线的上方,因此我们判断这个学生会被录取
这种方法叫做逻辑回归(Logistic Regression)
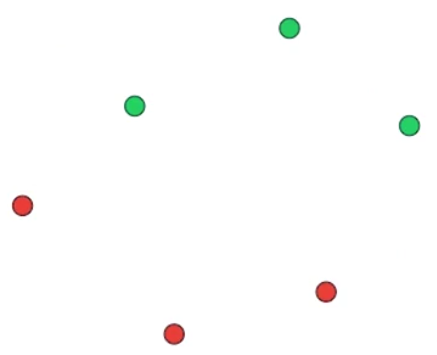
我们如何找到这条最好地分割数据点的线?,让我们看上图这个简单的例子
如何画出一条线以最好地区分绿色数据点和红色数据点
计算机无法依靠视觉来画出这条线,所以我们从画一条像这样的随机的线开始
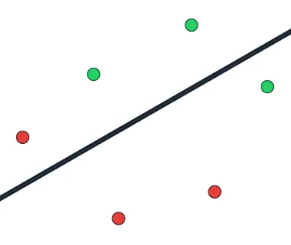
有了这条线,我们再随机地规定,位于线的上方的点为绿色,下方的点为红色
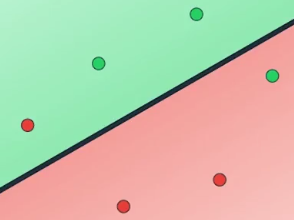
然后就像线性回归那样,我们先计算这条线的效果,一个简单的测量误差的标准是出错的数目
即被错误归类的数据点的数量,这条线错判了两个点,一个红色的点和一个绿色的点
因此我们说它有两个错误,仍然与线性回归类似,我们移动这条线
通过梯度下降算法(gradient descent)最小化错误数量
如果沿着这个方向稍微移动这条线,我们可以看到它开始能正确地归类其中一个数据点
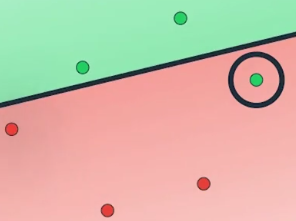
把错误数目降低到一个,如果继续移动这条线,它正确地归类了另一个点

错误数目被降低到了零
实际使用中,为了正确地使用梯度下降算法,我们需要最小化的并不是错误数目
取而代之的是,能代表错误数目的对数损失函数(log loss function)
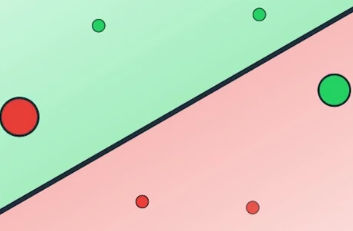
上图中有六个数据点,其中四个被正确分类,它们是两个红色和两个绿色
两个被错误归类,它们是一个红色和一个绿色
误差函数会对这两个被错误归类的数据点施加很大的惩罚,而对四个被正确归类的点施加很小的惩罚
在这门课中我们将会正式地学习误差函数公式
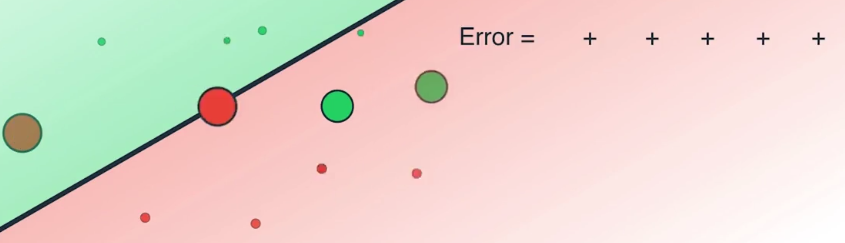
我们现在使用所有数据点的错误之和作为误差函数,我们得到了一个很大的误差值
因为两个被错判的点带来了很大的误差

如上图,现在四处移动这条线以将误差降到最小,如果我们沿着这个方向移动这条线
可以看到有些误差减小了,有些则微微增加了,但总体上,误差之和变小了
因为我们正确地归类了之前被错判的两个点

这个过程的意图是找出能最小化误差函数的最佳拟合线
我们如何最小化误差函数?依旧是使用梯度下降算法
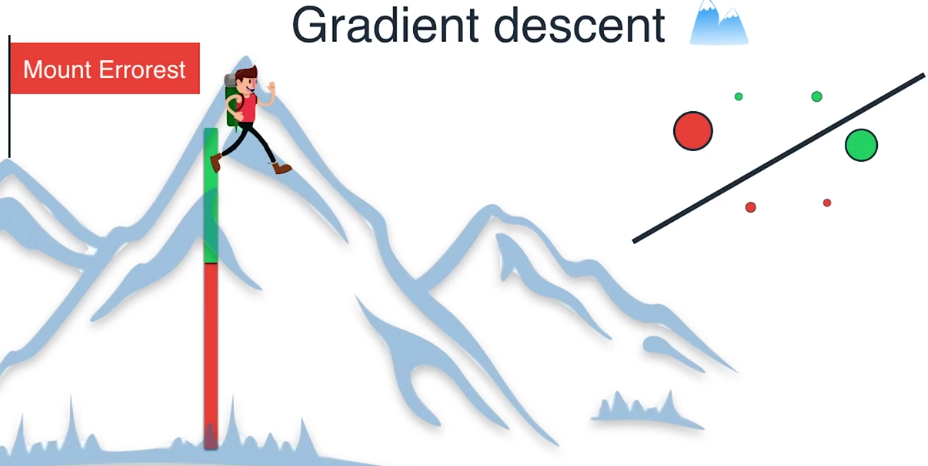
现在我们来到珠穆朗玛峰顶,我们所在的位置很高,因为此时有很大的误差
这可以从绿色和红色区域之和的大小中看出
我们探索四周寻找下降最大的方向 ,或者等价地寻找能通过移动直线最大程度减小误差的方向
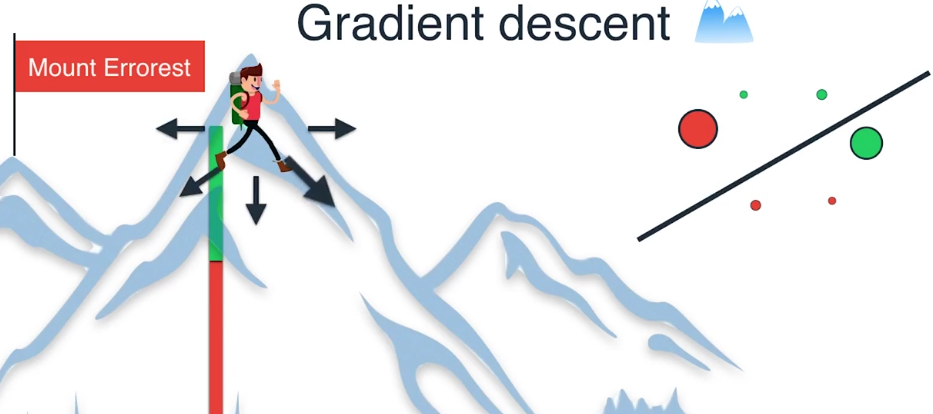
我们决定沿着这个方向前进一步,现在只有一个点被错误地归类
我们可以看到这种方法如何减小误差函数,把我们从山顶上带下来,
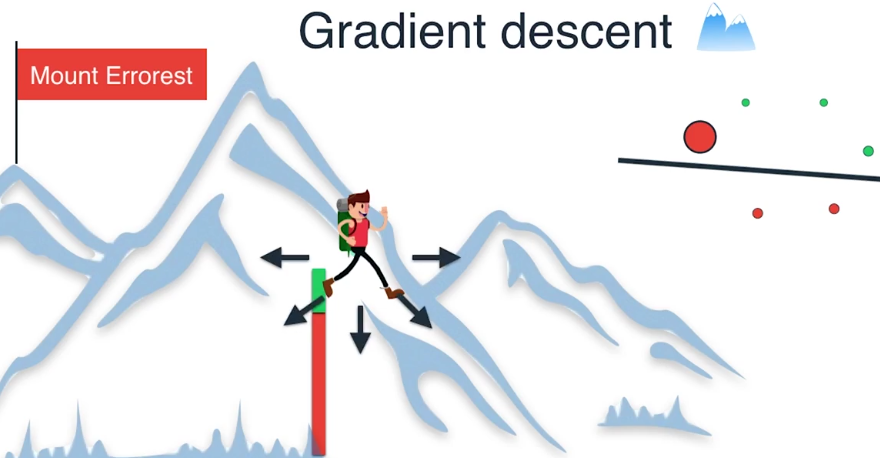
我们继续这样做,沿着最大程度减小误差的方向前进一步,就到达了山底
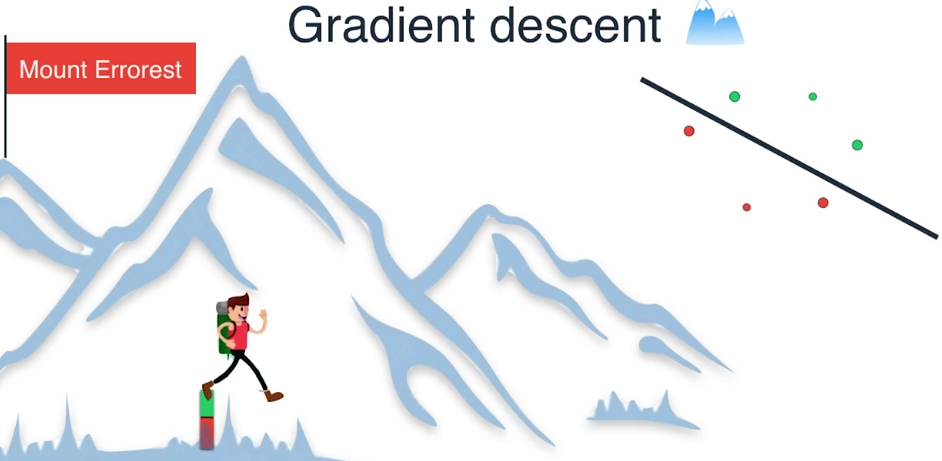
因为我们已经将误差减小到了最小值
Neural Networks
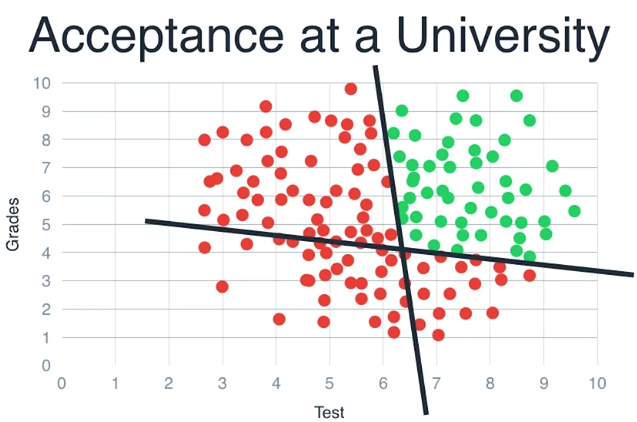
上图更加贴近真实的数据,低的测试分或者低的成绩的都不应该被接受
所以似乎一条线已经不能分离这些点了,用一个圆,或者两条线,也许能有效
让我们试一下两条线,我们能够怎么找到这两条线呢,再一次我们可以做这个
通过梯度下降来最小化一个和之前相似的对数损失函数,这被称为神经网络(Neural network)
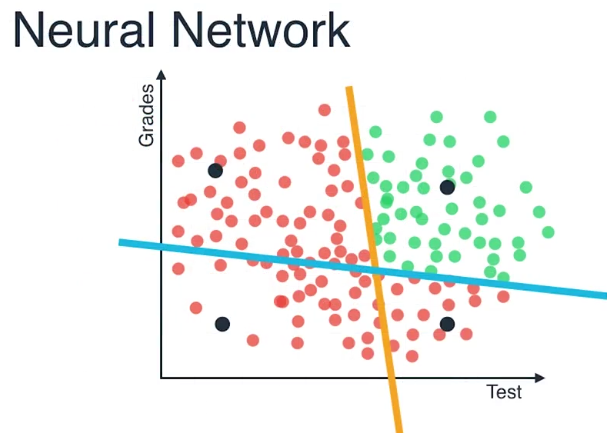
现在问题是为什么这被称为神经网络?
比如说我们在一台非常慢的电脑上面工作,一个时间仅仅能够处理一件事,所以非常不容易来问
右上方这个区域的点被两条线区分开了吗?我们必须要把这个分成两个单独的问题
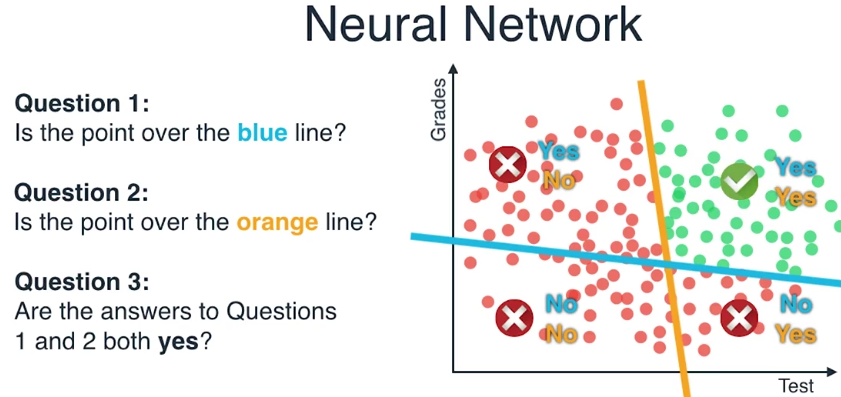
第一个问题是:这个点在这条蓝线之上吗?
让我们基于这个图上的4个黑点来回答这个问题,对于这四个点,我们能够看出
第二个问题是:这个点在这条橘色的线上面吗?
对于这4个点,我们能够看出这个答案是
第三个问题是:把前两个的答案取出来组合他们,第一个问题和第二个问题的答案都是对的吗?
对于这四个点,我们能够看出答案,除了在这个绿色区域的这个点,其他都是不对的
现在让我们取出每个问题作为一个小的笔记:
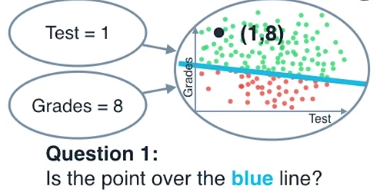
第一个问题是,这个点在蓝色的线之上吗?这个区域我们有一个节点和两个输入节点
测试得分和成绩,例如我们有一个学生,测试成绩是1,平时成绩是8,画出这个点
检查这个点是不是在这条蓝线上面,返回这个答案,yes or no
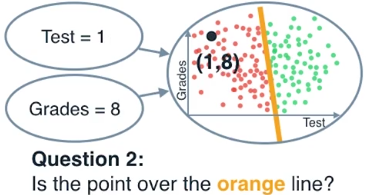
第二个问题是相似的,我们输入一个测试分数和成绩进入相应的节点,我们画出这个点
返回yes or no,依赖于这个点在橙色线的上面还是没有
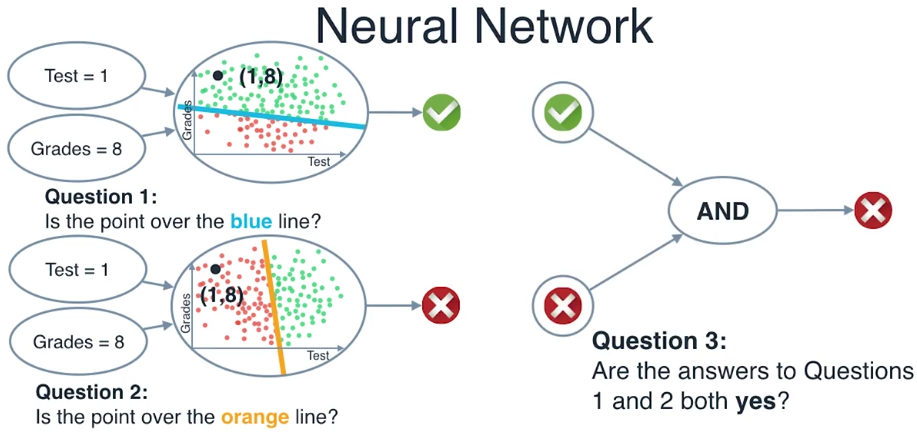
第三个问题是,问题1和问题2的答案都是对的吗?
我们将会把前面两个问题的答案作为输入,如果这两个答案都是对的,就返回对的,否则就返回错
这个在逻辑运算中称为 “和” 运算(and)
现在,这就是奇迹发生的地方,如果我们把这三个问题合在这个节点中,我们就得到了一个神经网络
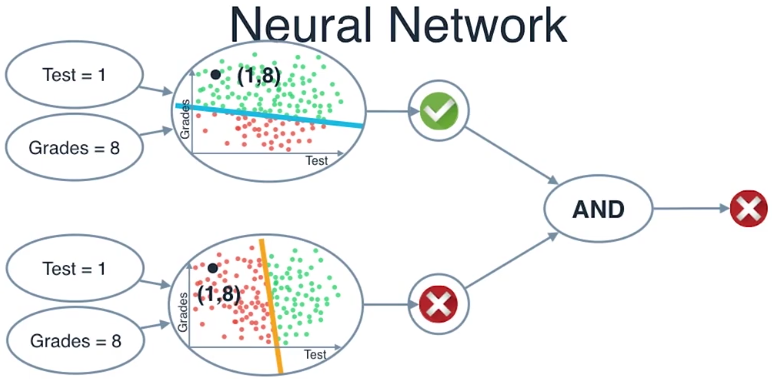
我们简化一下,就得到了下面的图
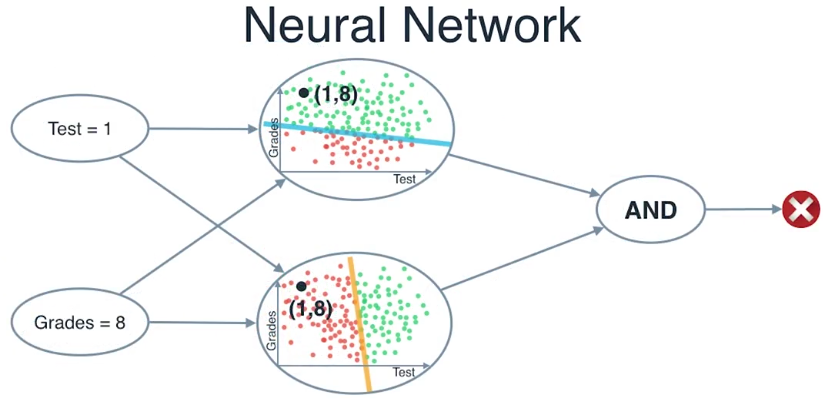
第一列是我们输入测试和成绩的地方,
第二列是我们检查这些和测试成绩有关的坐标点是否在每条线的上面
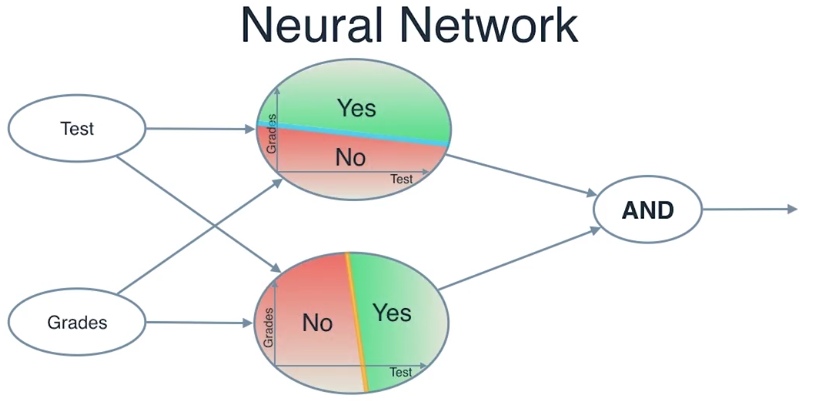
第三层,我们看看前面的层的答案,用“和”运算符把他们合在一起
那么这就是我们的神经网络的样子,现在你也许在想这些事有点让人怀疑
前面两个输出的错,看起来就像他们取值,然后检查是否相关的点在特定的直线上还是下
因此第三层仅仅是输入对或者错,然后返回对和错
有可能把第三层的节点看作是前面两层节点中的一个吗?答案是可以的
让我们来更进一步看看“和”运算符
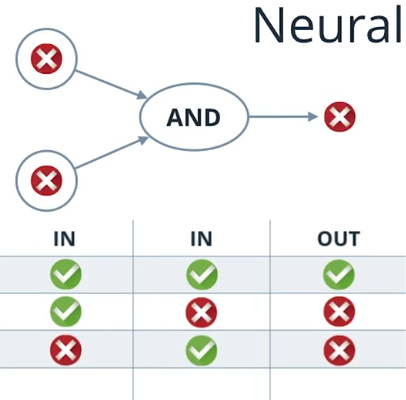
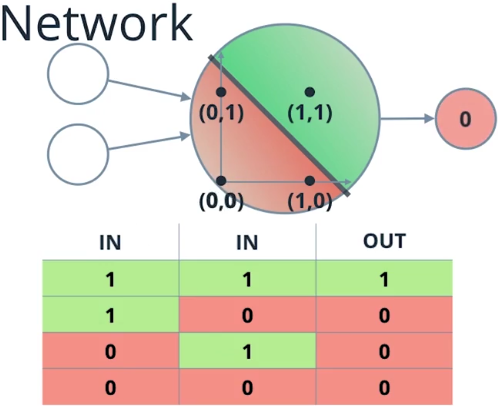
现在我们能够想象yes作为1, no作为0,这种情况下,上面的表格变成了另外一个
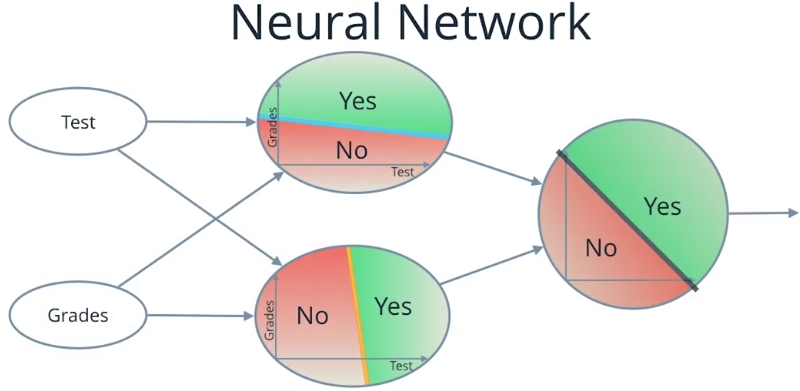
那么上图就是我们的最终的神经网络的样子
左边我们叫做输入层,我们输入测试分数和成绩,然后通过中间层
这被称为隐藏层,会帮助我们计算,所以在这里我们看到1和8一起变成了一个点,有着坐标1和8
在中间层的两幅图中,在上面的节点中(1,8)在绿色或者说在正的区域,所以这个点输出一个YES
在下面的点中(1,8)在红色或者在负的区域,所以底下的节点输出一个NO
现在我们记得对YES 替换成1,NO被0表示,现在下一层被成为输出层
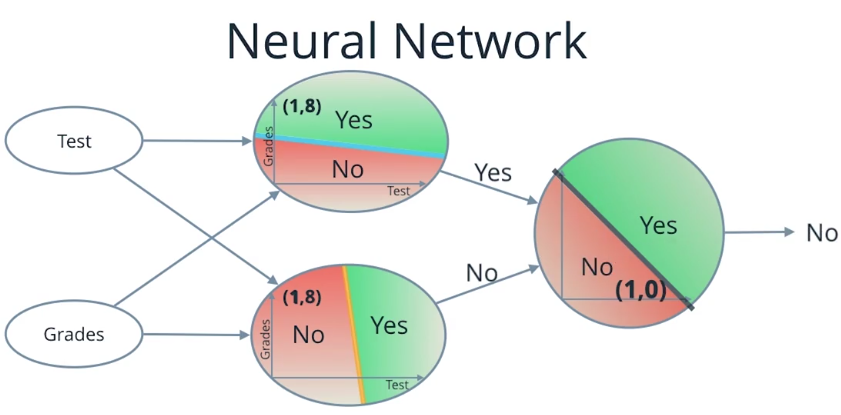
取值来自与中间层主要是1和0,它定位在坐标(1,0)这个点,这个点是在最后节点的红色
或者说是负的区域,所以输出一个NO,神经网络已经收到了这个输入
值为1的测试分数和值为8的成绩,它输出一个NO
这是一个简单的神经网络,但是你能够看出如何增加更多的节点在中间甚至是更多的节点层
可以帮助我们在平面上映射更加复杂的区域甚至在三维空间或者是更高维的空间
神经网络是非常强的机器学习算法 ,其被使用在大多数人工项目中比如面部识别、语音识别、下棋和自动驾驶
我们称它为神经网络是因为这些节点像 大脑里面的神经元,神经元将会把输入和其他神经元的输出以一种
神经脉冲的形势,决定是否激活这个神经脉冲,在我们的情况中,神经元把输入和其他神经元的输出以
数字的形式决定返回一个0或者是一个1