我们想要让涉及在损失函数计算中值不要太大或太小
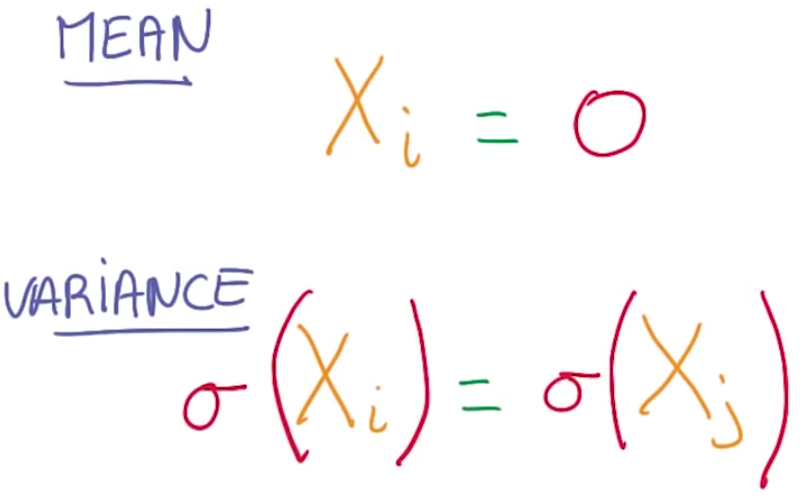
一个好的指导原则是 我们总是想要我们的变量 均值为零 并且尽可能同方差
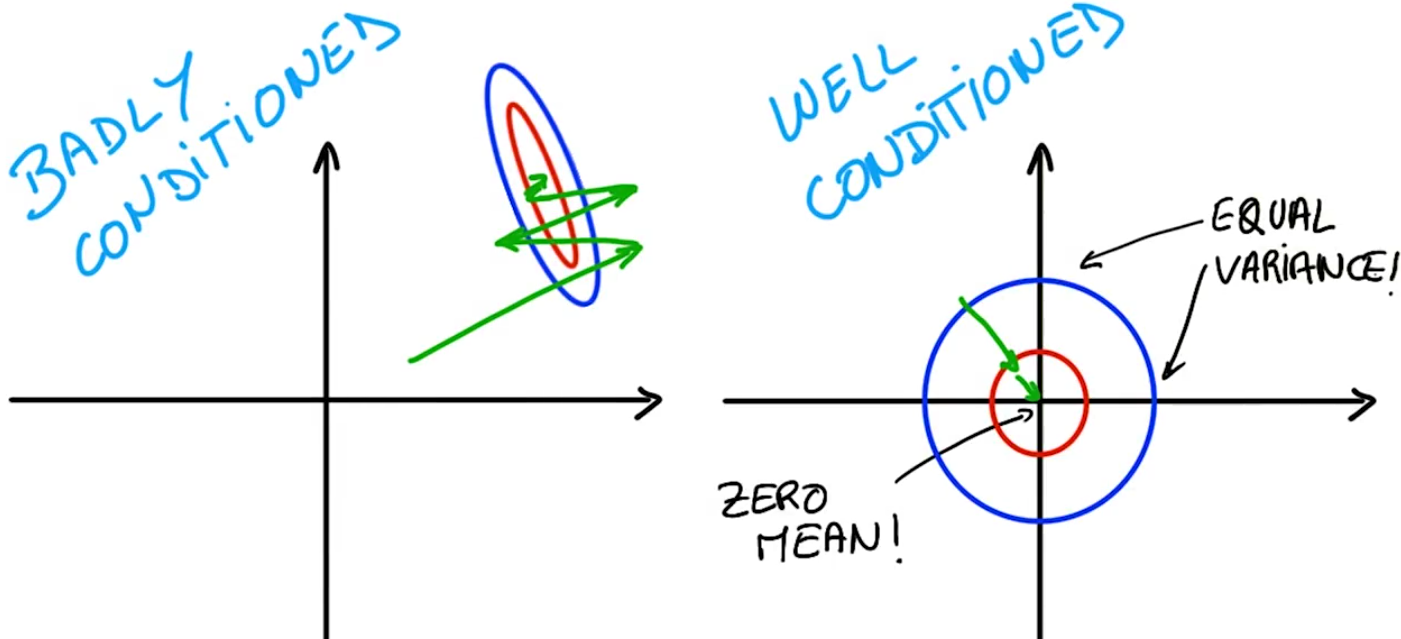
除了上面说的数值精度问题,当你在做最优化时,也有很好的数学理论让你保持你计算的值,具有均值为零与同方差的性质
在不理想的条件下意味着优化器得做很多搜索去找到一个好的解,如上左图
在理想的条件下优化器的工作简单很多

如果你处理图像,就比较简单,你可以取得你图像的像素值,他们通常在0-255之间,并且很容易减去128和除以128,这并没有改变你的图像的内容,但它更加适合数值优化
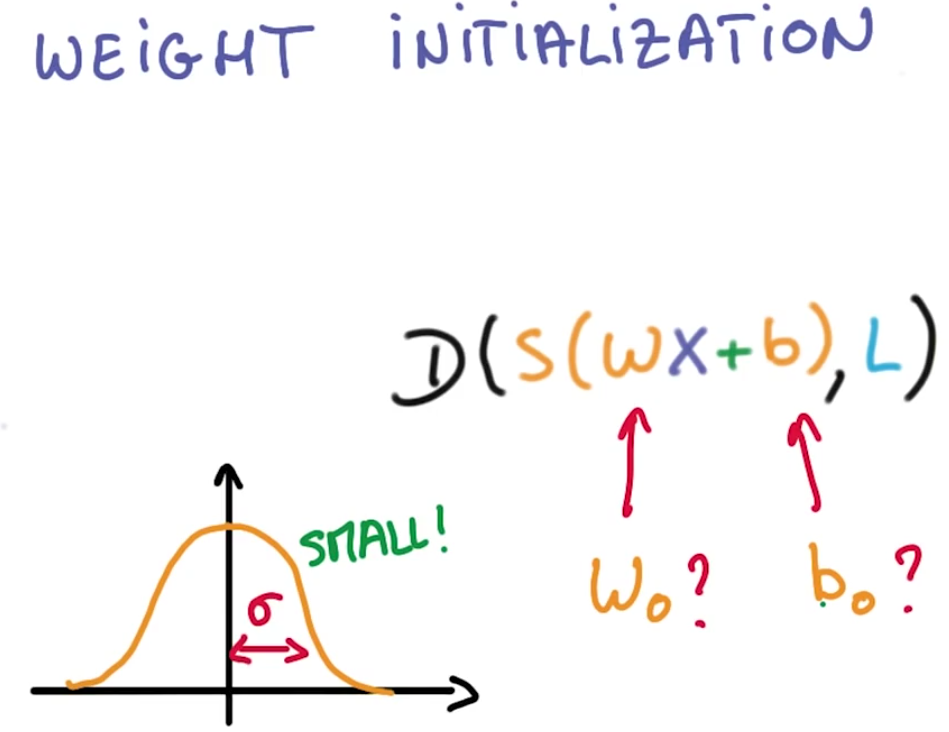
想让你的权重和偏差初始化在一个足够好的开始点在梯度下降过程中,有很多很好的机制去找到好的初始化值,但我们想聚焦在一个简单通用的方法上
从均值为0标准差为sigma 的搞死分布中随机抽样,作为初始权重值。sigma的值决定了最优化过程中,在初始点你输出的数量级。
因为上面的softmax这个数量级,也决定了你初始化概率分布的峰值,一个大的sigma意味着你的分布将有大的峰值,这将会很武断
一个小的sigma意味着你的分布是不确定的,通常比较好的是开始于一个不确定的分布,随着训练的程度让最优化变得越来越自信,
所以用一个小的sigma开始
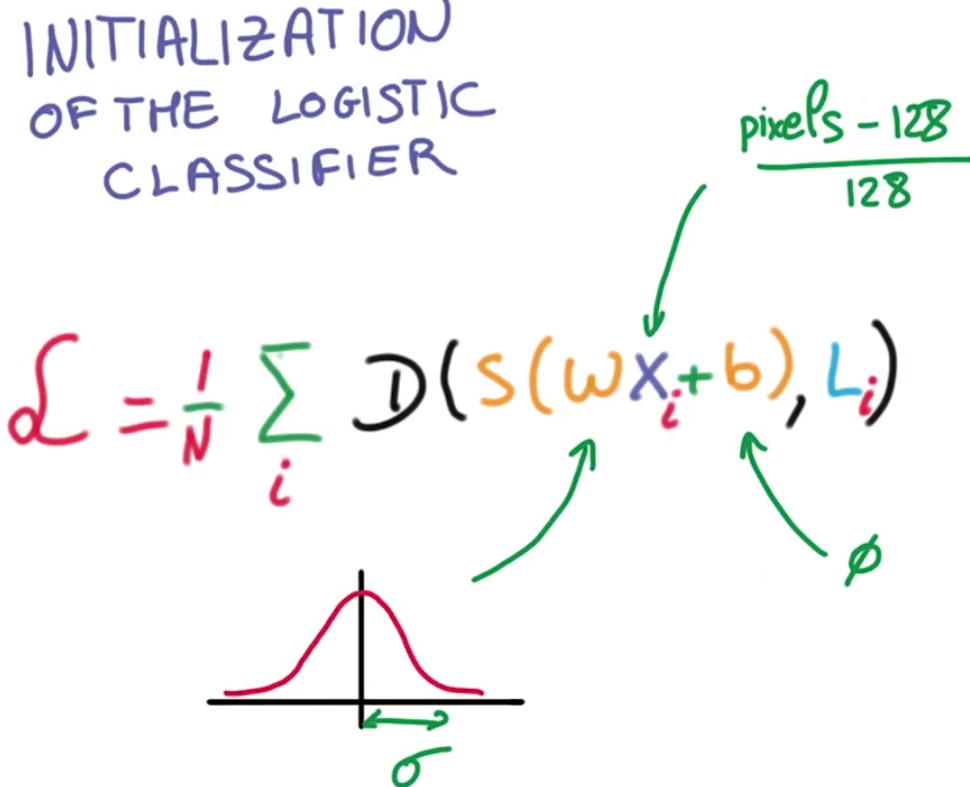
现在我们确实有了我们需要训练分类器的一起东西,我们得到了我们的训练数据 这些数据被标准化为零均值 和一致的方差
我们把它乘以一个大的矩阵,这个矩阵初始化为随机权重,我们使用softmax函数然后用交叉熵损失
我们计算在整个训练数据上的平均损失
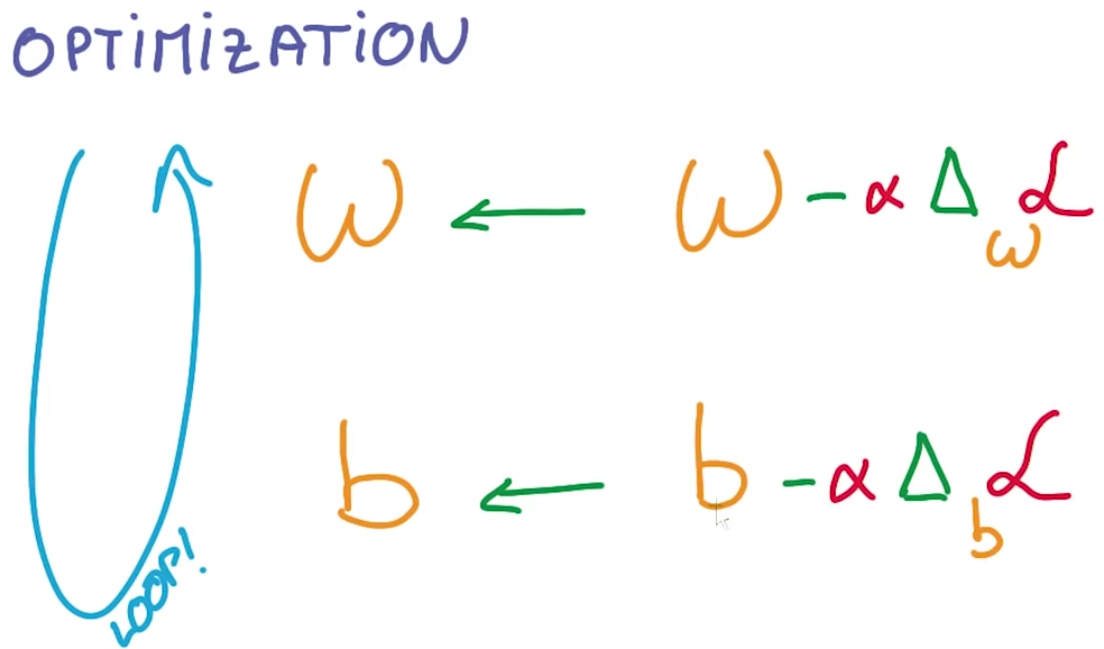
然后用我们神奇的最优化包,计算这个损失函数对权重和偏差的导数,接着沿着导数相反的方向后退一步,然后我们从头再来
并重复这个过程,直到我们达到损失函数的极小值