2020BUAA软工个人项目作业
17373010 杜博玮
| 项目 | 内容 |
|---|---|
| 这个作业属于哪个课程 | 2020春季计算机学院软件工程(罗杰 任健) |
| 这个作业的要求在哪里 | 个人项目作业 |
| 我在这个课程的目标是 | 学习软件工程,培养工程开发能力、团队协作能力,开阔视野 |
| 这个作业在哪个具体方面帮助我实现目标 | 通过个人尝试对软件工程构建一定认识 |
教学班级 005
项目地址 https://github.com/Cuogeihong/IntersectProject
PSP表格:
| PSP2.1 | Personal Software Process Stages | 预估耗时(分钟) | 实际耗时(分钟) |
|---|---|---|---|
| Planning | 计划 | ||
| Estimate | 估计这个任务需要多少时间 | 15 | 10 |
| Development | 开发 | ||
| Analysis | 需求分析 (包括学习新技术) | 80 | 90 |
| Design Spec | 生成设计文档 | 45 | 40 |
| Design Review | 设计复审 | 15 | 10 |
| Coding Standard | 代码规范 (为目前的开发制定合适的规范) | 15 | 10 |
| Design | 具体设计 | 60 | 75 |
| Coding | 具体编码 | 240 | 200 |
| Code Review | 代码复审 | 15 | 20 |
| Test | 测试(自我测试,修改代码,提交修改) | 120 | 150 |
| Reporting | 报告 | ||
| Test Reporting | 测试报告 | 45 | 40 |
| Size Measurement | 计算工作量 | 15 | 10 |
| Postmortem & Process Improvement Plan | 事后总结, 并提出过程改进计划 | 15 | 20 |
| 合计 | 680 | 675 |
解题思路:
我的思路主要是暴力求解。通过处理输入数据,将直线表示为(ax+by+c=0)的形式,将圆表示为((x-a)^2+(y-b)^2=r^2)的形式,使用vector数组储存。计算时分为三种情况,直线与直线之间,圆与直线之间,圆与圆之间,对这三种情况分别利用已经推导好的公式计算得出结果,将结果去重后得到答案。
通过数学知识我分析了暴力求交点的方法。
计算两直线之间的交点时先判断是否平行,之后直接代入两个二元一次方程联立后的解即可得到结果。
计算直线与圆之间的交点时首先判断直线是否垂直于x轴,如果是,则直接求出(x),此后解一元二次方程得到(y)。否则通过直线将(y)从圆的方程组消掉,求解一元二次方程得到(x),再代回直线求得(y)。
计算圆与圆之间交点直接将两圆相减得到直线方程,之后按照计算直线与圆之间的交点的方法求出圆与圆之间交点。此时需注意直线的(a)与(b)均为0的情况。
在后来优化代码时我发现了使用向量法求交点的方法,但是程序已经比较完善了,使用向量法需要几乎重写程序,因此我没有采用向量法。
设计实现过程:
主要功能在Image类中实现。main函数主要处理命令行参数以及接受输入并传给Image类。
Image类中主要有6个函数,其中addLine函数和addCircle函数处理输入数据并存储,getNum函数接受main函数调用并总领计算,getLineAndLinePoint,getLineAndCirclePoint,getCircleAndCirclePoint三个函数分别计算两直线之间的交点、直线与圆之间的交点、圆与圆之间交点。
此外程序定义了line、circle、point数据类型方便程序编写。
整体而言程序实现并不复杂。
单元测试主要测试以下功能。
-
两直线相交
-
两直线平行
-
三条直线相交于同一点
-
三条直线其中两直线平行
-
直线与圆相交
-
直线与圆相切
-
直线与圆相离
-
圆与圆外切
-
圆与圆相交
-
圆与圆外离
-
圆与圆内切
-
圆与圆内含
TEST_METHOD(TestMethod1) { // TODO: 在此输入测试代码 Image *img = new Image(); img->addLine(0, 0, 1, 1); img->addLine(1, -1, 0, 0); Assert::AreEqual(img->getNum(), 1); } TEST_METHOD(TestMethod2) { // TODO: 在此输入测试代码 Image *img = new Image(); img->addLine(0, 0, 1, 1); img->addLine(3, 4, 4, 5); Assert::AreEqual(img->getNum(), 0); } TEST_METHOD(TestMethod3) { // TODO: 在此输入测试代码 Image *img = new Image(); img->addLine(0, 0, 1, 1); img->addLine(-1, 1, 1, -1); img->addLine(3, 4, -3, -4); Assert::AreEqual(img->getNum(), 1); } TEST_METHOD(TestMethod4) { // TODO: 在此输入测试代码 Image *img = new Image(); img->addLine(0, 0, 1, 1); img->addLine(-1, 1, 1, -1); img->addLine(3, 4, -4, -3); Assert::AreEqual(img->getNum(), 2); } TEST_METHOD(TestMethod5) { // TODO: 在此输入测试代码 Image *img = new Image(); img->addCircle(0, 0, 1); img->addLine(0, 0, 1, 1); Assert::AreEqual(img->getNum(), 2); } TEST_METHOD(TestMethod6) { // TODO: 在此输入测试代码 Image *img = new Image(); img->addCircle(0, 0, 1); img->addLine(0, 1, 1, 1); Assert::AreEqual(img->getNum(), 1); } TEST_METHOD(TestMethod7) { // TODO: 在此输入测试代码 Image *img = new Image(); img->addCircle(0, 0, 1); img->addLine(2, 2, 2, 0); Assert::AreEqual(img->getNum(), 0); } TEST_METHOD(TestMethod8) { // TODO: 在此输入测试代码 Image *img = new Image(); img->addCircle(0, 0, 1); img->addCircle(2, 0, 1); Assert::AreEqual(img->getNum(), 1); } TEST_METHOD(TestMethod9) { // TODO: 在此输入测试代码 Image *img = new Image(); img->addCircle(0, 0, 1); img->addCircle(1, 0, 1); Assert::AreEqual(img->getNum(), 2); } TEST_METHOD(TestMethod10) { // TODO: 在此输入测试代码 Image *img = new Image(); img->addCircle(0, 0, 1); img->addCircle(3, 0, 1); cout << img->getNum() << endl; Assert::AreEqual(img->getNum(), 0); } TEST_METHOD(TestMethod11) { // TODO: 在此输入测试代码 Image *img = new Image(); img->addCircle(0, 0, 4); img->addCircle(3, 0, 1); cout << img->getNum() << endl; Assert::AreEqual(img->getNum(), 1); } TEST_METHOD(TestMethod12) { // TODO: 在此输入测试代码 Image *img = new Image(); img->addCircle(0, 0, 4); img->addCircle(0, 1, 1); cout << img->getNum() << endl; Assert::AreEqual(img->getNum(), 0); }单元测试运行结果:
性能分析与优化:
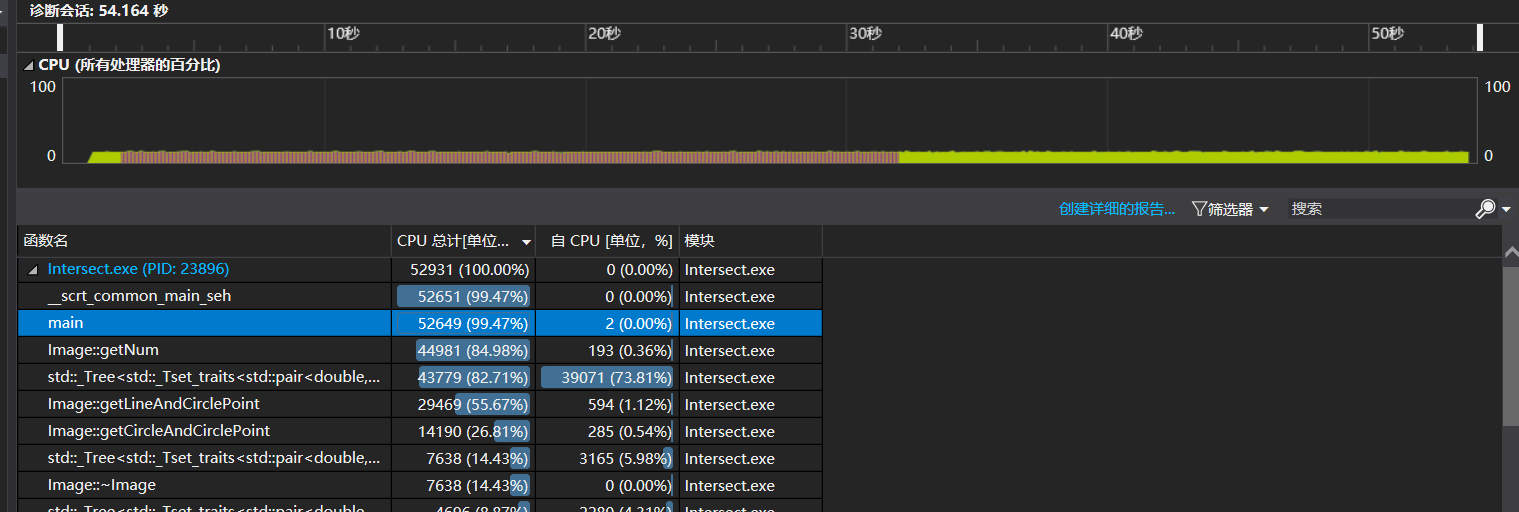
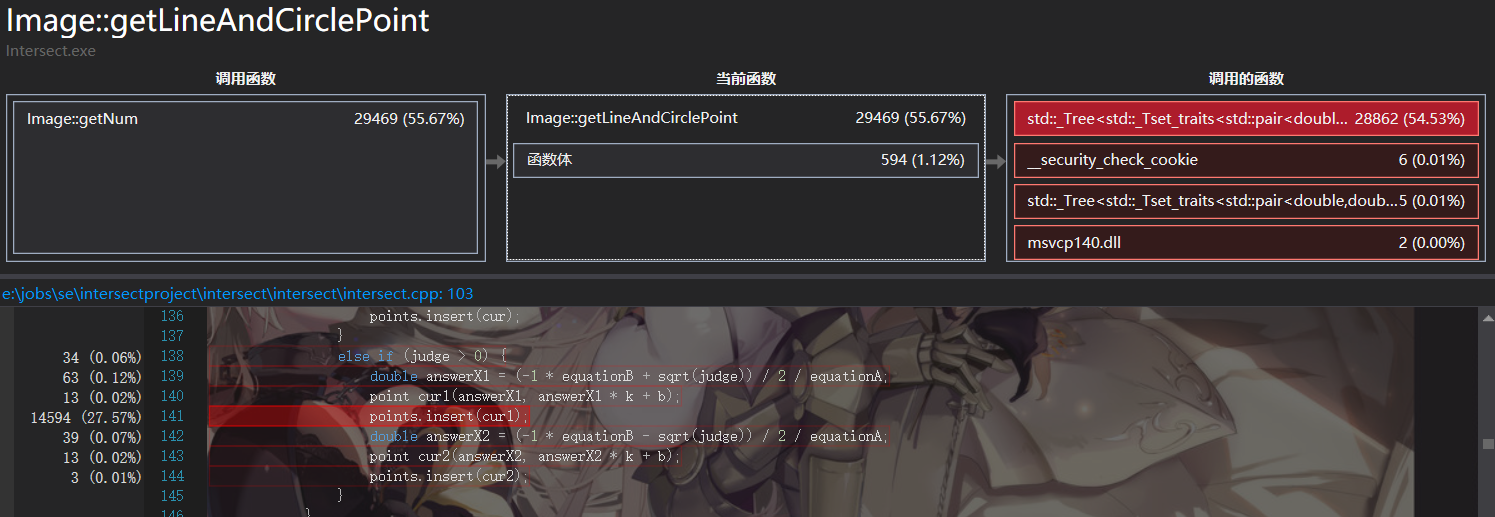
此前我采用set进行去重工作,通过性能分析我们可以看到,set花费了超过80%的CPU时间,因此需要对set进行优化。这样我找到了unordered_set,它利用hash来实现set的功能,不会对集合内数据进行排序,在修改后性能得到了大幅度的提高。
代码说明:
求两直线交点
for (int i = 0; i < linesLength; i++) {
for (int j = i + 1; j < linesLength; j++) {//避免重复运算
line lineA, lineB;
lineA = lines[i];
lineB = lines[j];
double judgeNum = lineA.a * lineB.b - lineA.b * lineB.a;//判断两直线是否平行
if (fabs(judgeNum) < 1e-8) {//防止因为浮点数以无限逼近于0代表0
continue;
}
double x, y;
x = (lineB.c * lineA.b - lineA.c * lineB.b) / judgeNum;//计算交点x
y = (lineB.a * lineA.c - lineA.a * lineB.c) / judgeNum;//计算交点y
point cur(x, y);
points.insert(cur);//将交点放入集合中去重
}
}
求直线与圆交点
for (int i = 0; i < linesLength; i++) {
for (int j = 0; j < circlesLength; j++) {
line curLine;
circle curCircle;
curLine = lines[i];
curCircle = circles[j];
if (curLine.b == 0) {//当直线垂直于x轴时
double distanceLC = curLine.c / curLine.a + curCircle.x;
if (fabs(fabs(distanceLC) - abs(curCircle.r)) < 1e-8) {
point cur(-1 * curLine.c / curLine.a, curCircle.y);
points.insert(cur);//将交点放入集合中去重
}
else if (fabs(distanceLC) - abs(curCircle.r) < 0) {
double sqrtTmp = sqrt(curCircle.r * curCircle.r -
distanceLC * distanceLC);
point cur1(-1 * curLine.c / curLine.a, curCircle.y + sqrtTmp);
point cur2(-1 * curLine.c / curLine.a, curCircle.y + sqrtTmp);
points.insert(cur1);//将交点放入集合中去重
points.insert(cur2);//将交点放入集合中去重
}
}
else {
//用x表示y的值 y=kx+b
double k = -1 * curLine.a / curLine.b, b = -1 * curLine.c / curLine.b;
double equationA, equationB, equationC;//表示化简得到的一元二次方程
equationA = k * k + 1;
equationB = 2 * (k * b - k * curCircle.y - curCircle.x);
equationC = curCircle.x * curCircle.x - curCircle.r * curCircle.r +
(b - curCircle.y) * (b - curCircle.y);
double judge = equationB * equationB - 4 * equationA * equationC;//判别式
if (fabs(judge) < 1e-8) {
//一元二次方程只有一个根时
double answerX = -1 * equationB / 2 / equationA;
point cur(answerX, answerX * k + b);
points.insert(cur);//将交点放入集合中去重
}
else if (judge > 0) {
//计算x的两个根并推出y的值
double answerX1 = (-1 * equationB + sqrt(judge)) / 2 / equationA;
point cur1(answerX1, answerX1 * k + b);
points.insert(cur1);//将交点放入集合中去重
double answerX2 = (-1 * equationB - sqrt(judge)) / 2 / equationA;
point cur2(answerX2, answerX2 * k + b);
points.insert(cur2);//将交点放入集合中去重
}
}
}
}
两圆之间交点的计算与直线与圆计算相同,不再放出。
消除 Code Quality Analysis 中的所有警告:
