奥运
Time Limit: 1000/1000 MS (Java/Others) Memory Limit: 65536/65536 K (Java/Others)
Total Submission(s): 2926 Accepted Submission(s): 739
Problem Description
北京迎来了第一个奥运会,我们的欢呼声响彻中国大地,所以今年的奥运金牌 day day up!
比尔盖兹坐上鸟巢里,手里摇着小纸扇,看的不亦乐乎,被俺们健儿的顽强拼搏的精神深深的感动了。反正我的钱也多的没地方放了,他对自己说,我自己也来举办一个奥运会,看谁的更火。不过他的奥运会很特别:
1 参加人员必须是中国人;
2 至少会加法运算(因为要计算本人获得的金牌数)
他 知道中国有很多的名胜古迹,他知道自己在t1 到 t2天内不可能把所有的地方都玩遍,所以他决定指定两个地方v1,v2,如果参赛员能计算出在t1到t2天(包括t1,t2)内从v1到v2共有多少种走 法(每条道路走需要花一天的时间,且不能在某个城市停留,且t1=0时的走法数为0),那么他就会获得相应数量的金牌,城市的总数<=30,两个城 市间可以有多条道路
,每条都视为是不同的。
比尔盖兹坐上鸟巢里,手里摇着小纸扇,看的不亦乐乎,被俺们健儿的顽强拼搏的精神深深的感动了。反正我的钱也多的没地方放了,他对自己说,我自己也来举办一个奥运会,看谁的更火。不过他的奥运会很特别:
1 参加人员必须是中国人;
2 至少会加法运算(因为要计算本人获得的金牌数)
他 知道中国有很多的名胜古迹,他知道自己在t1 到 t2天内不可能把所有的地方都玩遍,所以他决定指定两个地方v1,v2,如果参赛员能计算出在t1到t2天(包括t1,t2)内从v1到v2共有多少种走 法(每条道路走需要花一天的时间,且不能在某个城市停留,且t1=0时的走法数为0),那么他就会获得相应数量的金牌,城市的总数<=30,两个城 市间可以有多条道路
,每条都视为是不同的。
Input
本题多个case,每个case:
输入一个数字n表示有n条道路 0<n<10000
接下来n行每行读入两个数字 p1,p2 表示城市p1到p2有道路,并不表示p2到p1有道路 (0<=p1,p2<2^32)
输入一个数字k表示有k个参赛人员
接下来k行,每行读入四个数据v1,v2,t1,t2 (0<=t1,t2<10000)
输入一个数字n表示有n条道路 0<n<10000
接下来n行每行读入两个数字 p1,p2 表示城市p1到p2有道路,并不表示p2到p1有道路 (0<=p1,p2<2^32)
输入一个数字k表示有k个参赛人员
接下来k行,每行读入四个数据v1,v2,t1,t2 (0<=t1,t2<10000)
Output
对于每组数据中的每个参赛人员输出一个整数表示他获得的金牌数(mod 2008)
Sample Input
6
1 2
1 3
2 3
3 2
3 1
2 1
3
1 2 0 0
1 2 1 100
4 8 3 50
Sample Output
0
1506
0
Source
Recommend
lcy
先列出以下定义和定理
定义:设G=<V, E>是一个简单图,它有n个结点V={v1, v2, ... , vn },则n阶方阵A(G)=(aij)称为G的邻接矩阵。其中

adj表示邻接,nadj表示不邻接。
定理:设A(G)是图G的邻接矩阵,则(A(G))k 中的i行,j列元素aij(k)等于G中联结vi与vj的长度为k的路的数目。证明见《离散数学》左孝凌。
求第t天城市 i 到城市 j 共有多少种走法就是求城市 i 到城市 j 经过1~k条道路的路径方案数,
设第t天方案数为B(t),A为城市的邻接矩阵,有
![]()
那么t1到t2天(包括t1,t2)内从v1到v2的走法数目为B(t2)-B(t1-1),t1=0时特殊处理一下。
题意不是很明朗,需要注意的有
1. 城市的编号很大,但总数目<=30,要对城市重新编号。
2. 城市之间可能有重边。
3. B(t2)-B(t1-1)的结果可能小于零。
方法一:分块矩阵
建立下面分块矩阵,
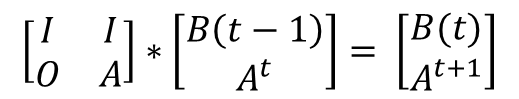
各个分块均为m*m的(m为城市个数),I为单位矩阵,O为零矩阵。
进一步得到,
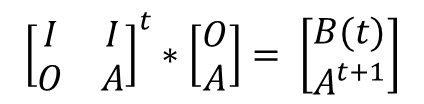
运用矩阵快速幂进行求解,

1 #include <iostream> 2 #include <algorithm> 3 #include <map> 4 #include <vector> 5 #include <functional> 6 #include <string> 7 #include <cstring> 8 #include <queue> 9 #include <set> 10 #include <cmath> 11 #include <cstdio> 12 using namespace std; 13 #define IOS ios_base::sync_with_stdio(false) 14 typedef long long LL; 15 const int INF = 0x3f3f3f3f; 16 17 const int modnum = 2008; 18 const int maxn = 61; 19 typedef struct matrix{ 20 int v[maxn][maxn]; 21 void init(){ memset(v, 0, sizeof(v)); } 22 }M; 23 M a, b, c, z, bn1, bn2, res1, res2; 24 25 M mul_mod(const M &a, const M &b, int L, int m, int n) 26 { 27 M c; c.init(); 28 for (int i = 0; i<L; i++){ 29 for (int j = 0; j<n; j++){ 30 for (int k = 0; k<m; k++)//注意j,k范围 31 c.v[i][j] = (c.v[i][j] + (a.v[i][k] * b.v[k][j] % modnum)) % modnum; 32 } 33 } 34 return c; 35 } 36 M power(M x, int L, int p) 37 { 38 M tmp; tmp.init(); 39 for (int i = 0; i<L; i++) 40 tmp.v[i][i] = 1; 41 while (p){ 42 if (p & 1) tmp = mul_mod(x, tmp, L, L, L); 43 x = mul_mod(x, x, L, L, L); 44 p >>= 1; 45 } 46 return tmp; 47 } 48 inline void init(int n) 49 { 50 b.init(); 51 for (int i = 0; i<n; i++) 52 b.v[i][i] = b.v[i][i + n] = 1; 53 c.init(); 54 for (int i = 0; i<n; i++) 55 for (int j = 0; j<n; j++) 56 b.v[i + n][j + n] = c.v[i + n][j] = a.v[i][j]; 57 z.init(); 58 } 59 int main() 60 { 61 int n, t1, t2, k, cnt, ans; 62 LL p1, p2; 63 map<LL, int> cm; 64 while (~scanf("%d", &n)){ 65 cm.clear(); 66 a.init(); 67 cnt = 0; 68 for (int i = 0; i<n; i++){ 69 scanf("%lld%lld", &p1, &p2); 70 if (!cm.count(p1)) cm[p1] = cnt++; 71 if (!cm.count(p2)) cm[p2] = cnt++; 72 a.v[cm[p1]][cm[p2]]++; 73 } 74 int num = cm.size(); 75 init(num); 76 scanf("%d", &k); 77 for (int i = 0; i<k; i++){ 78 scanf("%lld%lld%d%d", &p1, &p2, &t1, &t2); 79 if (t1>t2) swap(t1, t2); 80 if (!cm.count(p1) || !cm.count(p2)){ printf("0 "); continue; } 81 if(t1==0) res1=z;//z为零矩阵 82 else{ 83 bn1 = power(b, 2 * num, t1 - 1); 84 res1 = mul_mod(bn1, c, 2 * num, 2 * num, num); 85 } 86 if(t2==0) res2=z; 87 else{ 88 res2 = power(b, 2 * num, t2); 89 res2 = mul_mod(res2, c, 2 * num, 2 * num, num); 90 } 91 /* 92 因为t1<=t2 93 利用t1计算得到的结果在t2的结果,理想中可能会快一些 94 但测评系统运行时间仍然和直接计算t2一样 95 else if(t1!=0){ 96 bn2 = power(b, 2 * num, t2-t1+1); 97 bn2 = mul_mod(bn1, bn2, 2 * num, 2 * num, 2 * num); 98 res2 = mul_mod(bn2, c, 2 * num, 2 * num, num); 99 }else{ 100 bn2 = power(b, 2 * num, t2); 101 res2 = mul_mod(bn2, c, 2 * num, 2 * num, num); 102 } 103 */ 104 ans = (res2.v[cm[p1]][cm[p2]] - res1.v[cm[p1]][cm[p2]])%modnum; 105 while (ans<0) ans+=modnum; 106 printf("%d ", ans%modnum); 107 } 108 } 109 }
方法二
