UVA 10518 How Many Calls?

设g(x)为n=x时的调用次数，有Fabonacci数列递推式可以得到

g(x)=g(x-1)+g(x-2)+1，（f(x)要调用一次，所以要加1）。

转换为矩阵形式

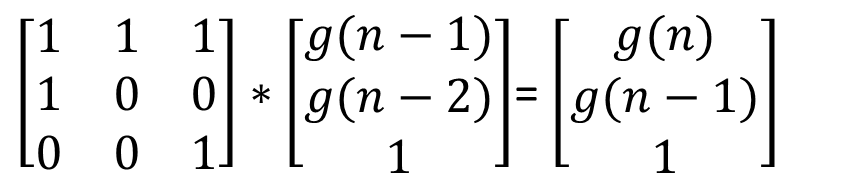
即，

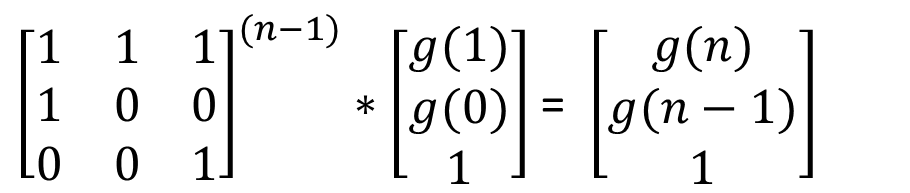
g(1)和g(0)均为1。

使用矩阵快速幂计算结果。

#include <iostream>
#include <algorithm>
#include <map>
#include <vector>
#include <functional>
#include <string>
#include <cstring>
#include <queue>
#include <set>
#include <cmath>
#include <cstdio>
using namespace std;
#define IOS ios_base::sync_with_stdio(false)
typedef long long LL;
const int INF=0x3f3f3f3f;

int modnum;
const int maxn=5;
typedef struct matrix{
    int v[maxn][maxn];
    void init(){memset(v,0,sizeof(v));}
}M;
M a,b;
M mul_mod(const M &a,const M &b,int L,int m,int n)
{
    M c; c.init();
    for(int i=0;i<L;i++){
        for(int j=0;j<n;j++){
            for(int k=0;k<m;k++)//注意j，k范围
                c.v[i][j]=(c.v[i][j]+(a.v[i][k]*b.v[k][j]%modnum))%modnum;
        }
    }
    return c;
}
M power(M x,int L,LL p)
{
    M tmp; tmp.init();
    for(int i=0;i<L;i++)
        tmp.v[i][i]=1;
    while(p){
        if(p&1) tmp=mul_mod(x,tmp,L,L,L);
        x=mul_mod(x,x,L,L,L);
        p>>=1;
    }
    return tmp;
}
inline void init()
{
    a.init();
    a.v[0][0]=a.v[0][1]=a.v[0][2]=a.v[1][0]=a.v[2][2]=1;
    b.init();
    b.v[0][0]=b.v[1][0]=b.v[2][0]=1;
}
int main()
{
    LL n;
    int ca=0;
    while(scanf("%lld%d",&n,&modnum)==2&&n+modnum){
        init();
        if(n<2){printf("Case %d: %lld %d %d
",++ca,n,modnum,1%modnum); continue;}
        a=power(a,3,n-1);
        a=mul_mod(a,b,3,3,1);
        printf("Case %d: %lld %d %d
",++ca,n,modnum,a.v[0][0]);
    }
}