Another kind of Fibonacci
Time Limit: 3000/1000 MS (Java/Others) Memory Limit: 65536/65536 K (Java/Others)
Total Submission(s): 2258 Accepted Submission(s): 900
Problem Description
As
we all known , the Fibonacci series : F(0) = 1, F(1) = 1, F(N) = F(N -
1) + F(N - 2) (N >= 2).Now we define another kind of Fibonacci : A(0)
= 1 , A(1) = 1 , A(N) = X * A(N - 1) + Y * A(N - 2) (N >= 2).And we
want to Calculate S(N) , S(N) = A(0)2 +A(1)2+……+A(n)2.
Input
There are several test cases.
Each test case will contain three integers , N, X , Y .
N : 2<= N <= 231 – 1
X : 2<= X <= 231– 1
Y : 2<= Y <= 231 – 1
Each test case will contain three integers , N, X , Y .
N : 2<= N <= 231 – 1
X : 2<= X <= 231– 1
Y : 2<= Y <= 231 – 1
Output
For each test case , output the answer of S(n).If the answer is too big , divide it by 10007 and give me the reminder.
Sample Input
2 1 1
3 2 3
Sample Output
6
196
Author
wyb
Source
Recommend
wxl
已知下列初始条件和递推式,求S(N)。

由于S(N)计算需要用到A(N)^2,计算A(N)^2,发现需要A(N-1)*A(N-2)的值,
而A(N-1)*A(N-2)可以由A(N-2)、A(N-3)运算得到。
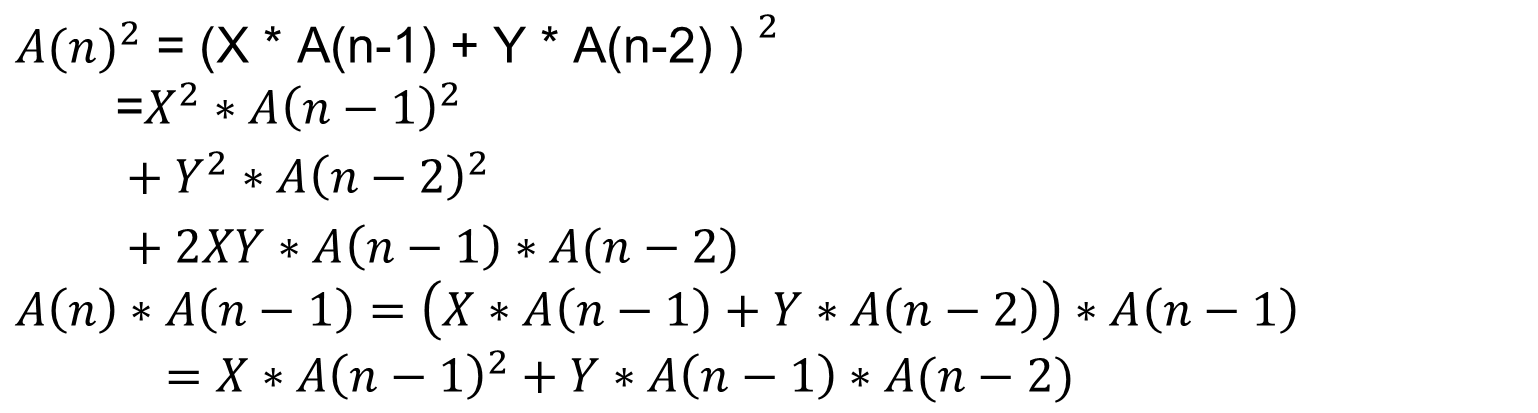
又有,
将以上式子列成矩阵

得到下面含幂次式子,以便使用快速幂优化计算过程,

使用矩阵乘法和矩阵快速幂实现程序,注意取模。
1 #include <iostream> 2 #include <algorithm> 3 #include <map> 4 #include <vector> 5 #include <functional> 6 #include <string> 7 #include <cstring> 8 #include <queue> 9 #include <set> 10 #include <cmath> 11 #include <cstdio> 12 using namespace std; 13 #define IOS ios_base::sync_with_stdio(false) 14 const int INF=0x3f3f3f3f; 15 16 const int maxn=4; 17 const int modnum=10007; 18 int N,X,Y,T; 19 typedef struct matrix{ 20 int v[maxn][maxn]; 21 void init(){memset(v,0,sizeof(v));} 22 }M; 23 M mul_mod(const M &a,const M &b,int L,int m,int n) 24 { 25 M c; c.init(); 26 for(int i=0;i<L;i++){ 27 for(int j=0;j<n;j++){ 28 for(int k=0;k<m;k++)//注意j,k范围 29 c.v[i][j]+=a.v[i][k]*b.v[k][j]; 30 c.v[i][j]%=modnum; 31 } 32 } 33 return c; 34 } 35 M power(M x,int L,int p) 36 { 37 M tmp; tmp.init(); 38 for(int i=0;i<L;i++) 39 tmp.v[i][i]=1; 40 while(p){ 41 if(p&1) tmp=mul_mod(x,tmp,L,L,L); 42 x=mul_mod(x,x,L,L,L); 43 p>>=1; 44 } 45 return tmp; 46 } 47 48 int main() 49 { 50 while(scanf("%d%d%d",&N,&X,&Y)==3){ 51 M b,a; 52 X%=modnum; Y%=modnum; 53 b.init(); 54 b.v[0][0]=2; 55 b.v[1][0]=b.v[2][0]=b.v[3][0]=1; 56 a.init(); 57 a.v[0][0]=a.v[2][1]=1; 58 a.v[0][1]=a.v[1][1]=X*X%modnum; 59 a.v[0][2]=a.v[1][2]=Y*Y%modnum; 60 a.v[0][3]=a.v[1][3]=2*X*Y%modnum; 61 a.v[3][1]=X; 62 a.v[3][3]=Y; 63 a=power(a,4,N-1); 64 a=mul_mod(a,b,4,4,1); 65 printf("%d ",a.v[0][0]); 66 } 67 return 0; 68 }