公式定理【】

文章目录

• 公式
• 两个重要极限公式
• 等价无穷小公式
• 三角函数的全名
• 导数公式
• 麦克劳林级数
• 其他常用公式
• 定理
• 罗尔定理
• 拉格朗日定理
• 柯西定理

公式

两个重要极限公式

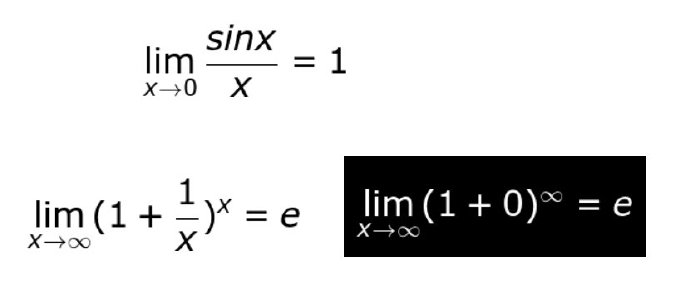
等价无穷小公式

当$x o 0$时：

• $ln (1+x)=x-frac{1}{2}x^{2}+frac{1}{3}x^{3}+O(x^{3})$

三角函数的全名

• 正弦：sine（简写sin）[sain]
• 余弦：cosine（简写cos）[kusain]
• 正切：tangent（简写tan）['tndnt]
• 余切：cotangent（简写cot）['ku’tndnt]
  $cot x=frac{1}{ an x}$
• 正割：secant（简写sec）['si:knt]
  $sec x=frac{1}{cos x}$
• 余割：cosecant（简写csc）['kau’si:knt]
  $csc x=frac{1}{sin x}$
• 正矢：versine（简写versin）['v:sain]
• 余矢：versed cosine（简写vercos）['v:s:d][kusain]

---

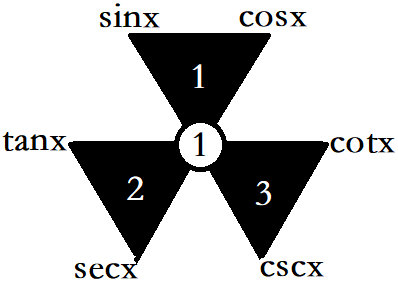
三个倒三角，两上角平方和等于下角平方。
$sin ^{2}x+cos ^{2}x=1$
$an ^{2}x+1=sec ^{2}x$
$1+cot ^{2}x=csc ^{2}x$

---

导数公式

$(log_{a}x)'=frac{1}{xln a}(a>0,a eq 1)$

$( an x)'=sec ^{2}x$
$(cot x)'=-csc ^{2}x$

$(sec x)'=sec x an x$
$(csc x)'=-csc xcot x$

$(arcsin x)'=frac{1}{sqrt{1-x^{2}}}$
$(arccos x)'=frac{-1}{sqrt{1-x^{2}}}$

$(arctan x)'=frac{1}{1+x^{2}}$
$( extrm{arccot} x)'=frac{-1}{1+x^{2}}$

麦克劳林级数

如果函数f(x)在点x=0处存在任意阶导数，则称$f(0)+f'(0)x+frac{f''(0)}{2!}x^{2}+...+frac{f^{(n)}(0)}{n!}x^{n}+...$为函数f(x)的麦克劳林公式，记作：$f(x)sim sum_{n=0}^{infty }frac{f^{(n)}(0)}{n!}x^{n}$

其他常用公式

• 两数和的幂的展开式
  • $(E+B)^{n} =sum_{k=0}^{n}C_{n}^{k}E^{n-k}B^{k}$
    $=E^{n}+nE^{n-1}B+frac{n(n-1)}{2!}E^{n-2}B^{2}+frac{n(n-1)(n-2)}{3!}E^{n-3}B^{3}+...+B^{n}$
• 差化积
  • $x^{n}-1 = (x-1)(x^{n-1}+x^{n-2}+...+x+1)$
  • $a^{3}-b^{3} = (a-b)(a^{2}+ab+b^{2})$

定理

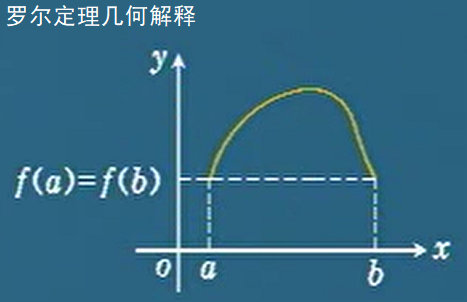
罗尔定理

若f(x)有：
1、在[a,b]上连续
2、在(a,b)上可导
3、f(a)=f(b)

那么，存在$xi in (a,b)，使f'(xi )=0$

拉格朗日定理

若f(x)有：
1、在[a,b]上连续
2、在(a,b)上可导

那么，存在$xi in (a,b)，使f '(ξ)=frac{f(b)-f(a)}{b-a}$
或写成：
1、$f(b)-f(a)=f'(xi )(b-a)$
2、$f(x)=f(a)+f'(xi )(x-a)$
3、$f(x)=f(a)+int_{a}^{x}f'(t)dt$

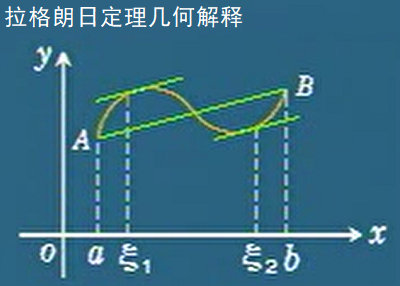
注：若f(a)=f(b)且a$eq$b，那么拉格朗日定理变成罗尔定理，即罗尔定理是拉格朗日定理的一种特殊情况。

柯西定理

若f(x)，g(x)有：
1、在[a,b]上连续
2、在(a,b)上可导
3、$g'(x) eq 0$

那么，存在ξ∈(a,b)，使$frac{f(b)-f(a)}{g(b)-g(a)}=frac{f'(xi )}{g'(xi )}$

注：若g(x)=x，则柯西定理变成拉格朗日定理。