▶ 给出四个整数,求他们是否能加减乘除括号拼凑成 24
● 代码,11 ms,正向枚举,推广性很强(nums 可以改为任意长度,也不限于拼凑 24 这个和),缺点是只能判定是否有解,不方便输出不重复的解
1 class Solution 2 { 3 public : 4 bool judgePoint24(vector<int>& nums) 5 { 6 vector<double> temp; 7 for (auto v : nums) 8 temp.push_back((double)v); 9 return solve(temp); 10 } 11 bool solve(vector<double> nums) 12 { 13 if (nums.size() == 0) 14 return false; 15 if (nums.size() == 1) 16 return abs(nums[0] - 24) < 1e-6; 17 18 int i, j, k; 19 vector<double> nums2; 20 for (i = 0; i < nums.size(); i++)// i 和 j 抢占两个元素 21 { 22 for (j = 0; j < nums.size(); j++) 23 { 24 if (i == j) 25 continue; 26 nums2.clear(); 27 for (k = 0; k < nums.size(); k++)// 把剩下两个元素放入 nums2 中 28 { 29 if (k != i && k != j) 30 nums2.push_back(nums[k]); 31 } 32 for (k = 0; k < 4; k++)// 尝试对 nums[i] 和 nums[j] 进行各种计算,结果放入 nums2 中 33 { 34 if (j > i && k < 2)// + 和 * 仅在 下标 j < i 的时候进行,这里 k 仅代表算符编号,不代表数组下标 35 continue; 36 if (k == 0) 37 nums2.push_back(nums[i] + nums[j]); 38 if (k == 1) 39 nums2.push_back(nums[i] * nums[j]); 40 if (k == 2) 41 nums2.push_back(nums[i] - nums[j]); 42 if (k == 3) 43 { 44 if (nums[j] != 0) 45 nums2.push_back(nums[i] / nums[j]); 46 else 47 continue; 48 } 49 if (solve(nums2))// 计算 nums2 中剩余项是否能凑 24 50 return true; 51 nums2.erase(nums2.end()-1);// 不能凑 24,把本次尝试的 nums[i] 和 nums[j] 的计算结果抹掉 52 } 53 } 54 } 55 return false; 56 } 57 };
● 分情况讨论,3 ms,代码非常暴力,仅适用于4元情况,不过可以通过添加新的函数 valid() 来支持更多的元
1 class Solution 2 { 3 public: 4 bool judgePoint24(vector<int>& nums) 5 { 6 sort(nums.begin(), nums.end()); 7 if (valid(nums)) 8 return true; 9 for(; next_permutation(nums.begin(), nums.end());) 10 { 11 if (valid(nums)) 12 return true; 13 } 14 return false; 15 } 16 bool valid(vector<int>& nums) 17 { 18 const double a = nums[0], b = nums[1], c = nums[2], d = nums[3]; 19 if (valid(a + b, c, d) || valid(a - b, c, d) || valid(a * b, c, d) || valid(a / b, c, d)) 20 return true; 21 if (valid(a, b + c, d) || valid(a, b - c, d) || valid(a, b * c, d) || valid(a, b / c, d)) 22 return true; 23 if (valid(a, b, c + d) || valid(a, b, c - d) || valid(a, b, c * d) || valid(a, b, c / d)) 24 return true; 25 return false; 26 } 27 bool valid(double a, double b, double c) 28 { 29 if (valid(a + b, c) || valid(a - b, c) || valid(a * b, c) || b && valid(a / b, c)) 30 return true; 31 if (valid(a, b + c) || valid(a, b - c) || valid(a, b * c) || c && valid(a, b / c)) 32 return true; 33 return false; 34 } 35 bool valid(double a, double b) 36 { 37 if (abs(a + b - 24.0) < 0.0001 || abs(a - b - 24.0) < 0.0001 || abs(a * b - 24.0) < 0.0001 || b && abs(a / b - 24.0) < 0.0001) 38 return true; 39 return false; 40 } 41 };
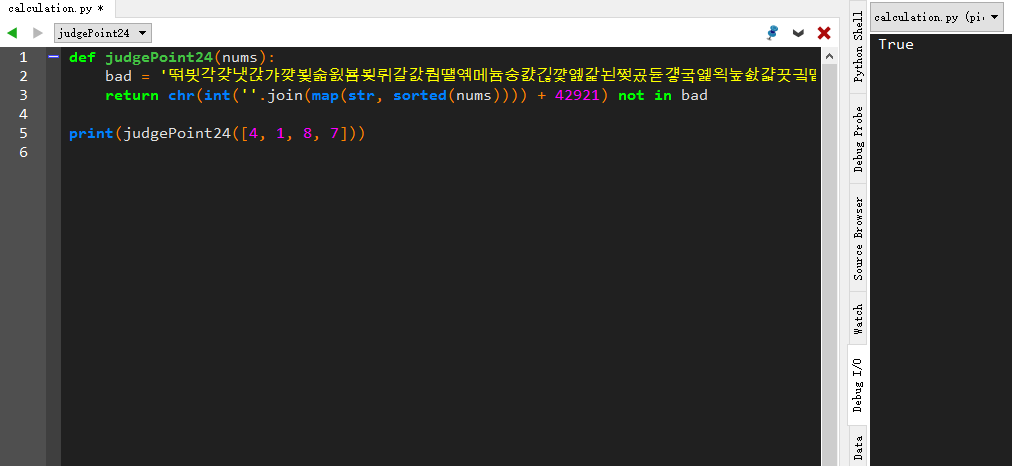
● 收录一个 python 的神奇的方法,大意是所有 495 种计算组合中有 404 种可解,91种不可解。把这 91 种无解的情况的 4 个数字从小大排序为一个四位数,加上特定的偏移量(代码中的 42921 和 19968)后转化为 Unicode 的一个字符保存起来,每次判定的时候只要检查所给的四个数字按上述方法转化城的字符是否在表中即可,时间复杂度 O(1),方法不可扩展
1 def judgePoint24(nums): 2 bad = '떢븻각걎냇갅갸꺚뵟숣욄뵴뵞뤼갈갌뤔떌옊메늄숭캸긶꺛옖갍뇐쩢곴듇걯궄옕왹눞솴걃끗긬땉궿가쌀낐걄숤뺴늘걘꽸숢걂갋갃쫐꼔솾쩡쇔솿끛뤜간븺쩬웨딴옠뤛갂뵪덠놤빐옋귒늂갰갖놥궾갆옌뼘묰거갎긷낤겼' 3 return chr(int(''.join(map(str, sorted(nums)))) + 42921) not in bad 4 5 def judgePoint24(nums): 6 bad = '对撒剘劥圞剜劏哱掶桺泛揋掵従剟剣彫寣污悫壛梄甏咍哲汭剤堧点卋嬞勆叛汬泐塵栋劚嚮咃宠吖剗楗囧力桻攋壯劯嗏桹劙剢剚焧啫栕炸栫栖嚲彳剛撑烃洿宋汷彲剙揁妷埻撧汢吩壙劇剭埼吕剝汣敯憇勇剥咎囻匓' 7 return chr(int(''.join(map(str, sorted(nums)))) + 19968) not in bad
■ 实测有效: