▶ 终于把之前的单隐层感知机改成了支持任意层数神经元的网络
● 代码,参考【https://www.zybuluo.com/hanbingtao/note/476663】(原文错误太多,几乎是重写了)。采用了 class FullConnectedLayer 封装同一层的多个神经元,采用 class Network 封装所有神经元层,包含了相应的前向、后向等计算方法
1 import numpy as np 2 from functools import reduce 3 import matplotlib.pyplot as plt 4 import matplotlib.ticker as ticker 5 from mpl_toolkits.mplot3d import Axes3D 6 from mpl_toolkits.mplot3d.art3d import Poly3DCollection 7 from matplotlib.patches import Rectangle 8 from datetime import datetime as dt 9 10 global_dataSize = 1000 # 总数据大小 11 global_trainRatio = 0.3 # 训练集占比 12 global_ita = 0.4 # 学习率 13 global_epsilon = 0.01 # 单轮累计误差要求 14 global_maxTurn = 300 # 最大训练轮数 15 16 def dataSplit(data, part): # 将数据集分割 17 return data[0:part,:],data[part:,:] 18 19 def myColor(x): # 颜色函数,用于对散点染色 20 r = np.select([x < 1/2, x < 3/4, x <= 1, True],[0, 4 * x - 2, 1, 0]) 21 g = np.select([x < 1/4, x < 3/4, x <= 1, True],[4 * x, 1, 4 - 4 * x, 0]) 22 b = np.select([x < 1/4, x < 1/2, x <= 1, True],[1, 2 - 4 * x, 0, 0]) 23 return [r,g,b] 24 25 class Activator(object): # 激活函数类,采用 sigmoid 函数 26 def σ(self, x): 27 return 1.0 / (1.0 + np.exp(-x)) 28 def dσ(self, x): 29 return x * (1.0 - x) # 注意输入的 x 是原神经元的输出值而不是激活前的值 30 31 def createData(dimIn, dimOut, len, linear): # 生成测试数据 32 np.random.seed(103) 33 inputData = np.random.rand(len, dimIn) 34 if linear: 35 transform = np.random.rand(dimIn, dimOut) # 线性变换 36 outputData = np.matmul(inputData,transform) # 线性变换 37 #print(transform) # 输出变换矩阵 38 else: 39 outputData = np.array(list( map(lambda x: [ np.sum(x**k) for k in range(1,dimOut+1) ], inputData) )) # 非线性变换 40 return inputData, outputData 41 42 class FullConnectedLayer(object): # 全连接层类 43 def __init__(self, dimIn, dimOut, activator): # 构造函数 44 self.dimIn = dimIn # 本层输入向量的维度 45 self.dimOut = dimOut # 本层输出向量的维度 46 self.activator = activator # 激活函数 47 self.W = np.random.uniform(-0.1, 0.1,(dimOut, dimIn)) # 权重数组 48 self.b = np.zeros(dimOut) # 偏置项 49 self.output = np.zeros((dimOut, 1)) # 输出向量 50 51 def forward(self, xArray): # 前向计算 52 self.input = xArray 53 self.output = self.activator.σ(np.dot(self.W, xArray) + self.b) 54 return self.output 55 56 def backward(self, wMultiplyDeltaNextLayer, isLastLayer): # 反向计算,输入上一层的误差项 57 if isLastLayer: 58 self.delta = self.activator.dσ(self.output) * wMultiplyDeltaNextLayer 59 else: 60 self.delta = self.activator.dσ(self.output) * wMultiplyDeltaNextLayer 61 self.W_grad = np.matmul(np.mat(self.delta).T, np.mat(self.input)) 62 self.b_grad = self.delta 63 return np.matmul(self.W.T, self.delta) # 返回乘积,方便上一层神经元计算 delta 64 65 def update(self, ita): # 梯度下降算法更新权重 66 self.W += ita * self.W_grad 67 self.b += ita * self.b_grad 68 #return self.W, self.b 69 70 class Network(object): # 神经网络类 71 def __init__(self, layers): 72 self.layers = [] 73 for i in range(len(layers) - 1): 74 self.layers.append(FullConnectedLayer(layers[i], layers[i+1], Activator())) 75 76 def predict(self, sample): # 计算单个样本的结果 77 temp = sample 78 for layer in self.layers: 79 temp = layer.forward(temp) 80 return temp 81 82 def train(self, x, y, ita, maxTurn, enablePrint): 83 row, dimOut = np.shape(y) 84 errorTable = np.zeros([row,dimOut]) 85 for turn in range(maxTurn): 86 for i in range(len(x)): 87 res = self.predict(x[i]) # 当前样本在当前网络上的结果,副作用更新各 layer 数据 88 errorTable[i] = y[i] - res 89 res = self.layers[-1].backward(errorTable[i], True) # 最后一层神经元的 delta 90 for layer in self.layers[-2::-1]: # 倒着计算各层 delta 91 res = layer.backward(res, False) 92 for layer in self.layers: # 正着调整各层权值 93 layer.update(ita) 94 errorRatio = np.sum(errorTable**2) / (row * dimOut) 95 if enablePrint and (turn == 0 or turn == maxTurn-1 or errorRatio < global_epsilon): 96 print( '%s turn %3d, errorRatio = %f' % (dt.now(), turn, errorRatio) ) 97 if errorRatio < global_epsilon: 98 break 99 100 def test(dimArray, linear = True, dataSize = global_dataSize, trainRatio = global_trainRatio, ita = global_ita, maxTurn = global_maxTurn): # 测试函数,给定每层神经元个数 101 allInData, allOutData = createData(dimArray[0], dimArray[-1], dataSize, linear) # 创建数据 102 trainInData, testInData = dataSplit(allInData, int(dataSize * trainRatio)) 103 trainOutData, testOutData = dataSplit(allOutData, int(dataSize * trainRatio)) 104 105 network = Network(dimArray) # 创建神经网络 106 107 network.train(trainInData, trainOutData, ita, maxTurn, True) # 训练神经网络 108 109 myResult = [ network.predict(sample) for sample in testInData ] # 在测试集上计算结果 110 111 errorTable = np.sum((np.array(myResult) - testOutData)**2, 1) 112 errorMax = np.max(errorTable) 113 errorRatio = np.sum(errorTable) / (dataSize*(1 - trainRatio) * dimArray[-1]) # 计算测试集错误率 114 print( "dimArray = %s, errorRatio = %f " % (dimArray, round(errorRatio,4)) ) 115 116 if dimArray[0] >= 4: # 画图部分,4维以上不画图,只输出测试错误率 117 return 118 119 fig = plt.figure(figsize=(10, 8)) 120 cm = plt.cm.get_cmap('gist_rainbow') 121 122 if dimArray[0] == 1: 123 plt.xlim(0.0,1.0) 124 plt.ylim(-0.15,0.15) 125 plt.scatter(testInData,np.zeros(len(testInData)), facecolors='none',c = errorTable, vmin = 0, vmax = max(errorTable),cmap = cm,s = 10) 126 plt.colorbar(ticks = np.linspace(0, max(errorTable), 5)) 127 plt.text(0.8, 0.1, "errorRatio = " + str(round(errorRatio,4)) + " maxError^2 = " + str(round(errorMax,3)), 128 size = 15, ha="center", va="center", bbox=dict(boxstyle="round", ec=(1., 0.5, 0.5), fc=(1., 1., 1.))) 129 130 if dimArray[0] == 2: 131 plt.xlim(0.0,1.0) 132 plt.ylim(0.0,1.0) 133 plt.scatter(testInData[:,0],testInData[:,1], facecolors='none',c = errorTable, vmin = 0, vmax = max(errorTable),cmap = cm,s = 10) 134 plt.colorbar(ticks = np.linspace(0, max(errorTable), 5)) 135 plt.text(0.2, 0.95, "errorRatio = " + str(round(errorRatio,4)) + " maxError^2 = " + str(round(errorMax,3)), 136 size = 15, ha="center", va="center", bbox=dict(boxstyle="round", ec=(1., 0.5, 0.5), fc=(1., 1., 1.))) 137 138 if dimArray[0] == 3: 139 ax = Axes3D(fig) 140 ax.set_xlim3d(0.0, 1.0) 141 ax.set_ylim3d(0.0, 1.0) 142 ax.set_zlim3d(0.0, 1.0) 143 ax.set_xlabel('X', fontdict={'size': 15, 'color': 'k'}) 144 ax.set_ylabel('Y', fontdict={'size': 15, 'color': 'k'}) 145 ax.set_zlabel('Z', fontdict={'size': 15, 'color': 'k'}) 146 sc = ax.scatter(testInData[:,0],testInData[:,1], testInData[:,2], c = errorTable, vmin = 0, vmax = max(errorTable),cmap = cm, s = 10) 147 plt.colorbar(sc, cax = fig.add_axes([0.05,0.1,0.02,0.8]), ticks = np.linspace(0, max(errorTable), 5)) 148 ax.text3D(0.8, 1, 1.15, "errorRatio = " + str(round(errorRatio,4)) + " maxError^2 = " + str(round(errorMax,3)), 149 size = 12, ha="center", va="center", bbox=dict(boxstyle="round", ec=(1, 0.5, 0.5), fc=(1, 1, 1))) 150 151 fig.savefig("R:\dimIn" + str(dimArray) + str(linear) + ".png") 152 plt.close() 153 154 if __name__ == '__main__': 155 test((1,3,1), True) 156 test((1,3,1), False) 157 158 test((2,3,2), True) 159 test((2,3,2), False) 160 test((2,10,2), False) 161 162 test((3,3,2), True) 163 test((3,10,2), True) 164 test((3,3,2), False) 165 test((3,10,2), False) 166 167 test((4,3,2), True) 168 test((4,3,2), False) 169 170 test((2,4,3,2), False) 171 test((3,4,3,2), True) 172 test((3,4,3,2), False) 173 test((4,6,3,3,2), True) 174 test((4,6,3,3,2), False)
● 输出结果
2019-09-21 17:29:34.113820 turn 0, errorRatio = 0.016535 2019-09-21 17:29:34.811177 turn 8, errorRatio = 0.009880 dimArray = (1, 3, 1), errorRatio = 0.010400 2019-09-21 17:29:35.501720 turn 0, errorRatio = 0.080407 2019-09-21 17:29:36.152499 turn 8, errorRatio = 0.007243 dimArray = (1, 3, 1), errorRatio = 0.005900 2019-09-21 17:29:36.666430 turn 0, errorRatio = 0.033850 2019-09-21 17:29:37.292406 turn 8, errorRatio = 0.007348 dimArray = (2, 3, 2), errorRatio = 0.005600 2019-09-21 17:29:37.836257 turn 0, errorRatio = 0.176799 2019-09-21 17:30:01.532073 turn 299, errorRatio = 0.054540 dimArray = (2, 3, 2), errorRatio = 0.057900 2019-09-21 17:30:02.095402 turn 0, errorRatio = 0.174731 2019-09-21 17:30:26.013079 turn 299, errorRatio = 0.054420 dimArray = (2, 10, 2), errorRatio = 0.057800 2019-09-21 17:30:26.522060 turn 0, errorRatio = 0.108589 2019-09-21 17:30:50.394160 turn 299, errorRatio = 0.041377 dimArray = (3, 3, 2), errorRatio = 0.046000 2019-09-21 17:30:51.152020 turn 0, errorRatio = 0.105360 2019-09-21 17:31:14.782947 turn 299, errorRatio = 0.041334 dimArray = (3, 10, 2), errorRatio = 0.046000 2019-09-21 17:31:15.476451 turn 0, errorRatio = 0.381080 2019-09-21 17:31:39.135285 turn 299, errorRatio = 0.300513 dimArray = (3, 3, 2), errorRatio = 0.320200 2019-09-21 17:31:39.871999 turn 0, errorRatio = 0.372009 2019-09-21 17:32:03.424233 turn 299, errorRatio = 0.300301 dimArray = (3, 10, 2), errorRatio = 0.320200 2019-09-21 17:32:04.101851 turn 0, errorRatio = 0.277614 2019-09-21 17:32:27.685676 turn 299, errorRatio = 0.228789 dimArray = (4, 3, 2), errorRatio = 0.235300 2019-09-21 17:32:27.822091 turn 0, errorRatio = 0.933335 2019-09-21 17:32:51.404807 turn 299, errorRatio = 0.893136 dimArray = (4, 3, 2), errorRatio = 0.914600 2019-09-21 17:32:51.572806 turn 0, errorRatio = 0.178735 2019-09-21 17:33:26.344111 turn 299, errorRatio = 0.054565 dimArray = (2, 4, 3, 2), errorRatio = 0.057900 2019-09-21 17:33:26.901960 turn 0, errorRatio = 0.110790 2019-09-21 17:34:01.600245 turn 299, errorRatio = 0.041538 dimArray = (3, 4, 3, 2), errorRatio = 0.046300 2019-09-21 17:34:02.336221 turn 0, errorRatio = 0.384966 2019-09-21 17:34:37.024351 turn 299, errorRatio = 0.302855 dimArray = (3, 4, 3, 2), errorRatio = 0.322500 2019-09-21 17:34:37.790311 turn 0, errorRatio = 0.278739 2019-09-21 17:35:25.160092 turn 299, errorRatio = 0.256081 dimArray = (4, 6, 3, 3, 2), errorRatio = 0.262400 2019-09-21 17:35:25.385607 turn 0, errorRatio = 0.934552 2019-09-21 17:36:12.910735 turn 299, errorRatio = 0.893136 dimArray = (4, 6, 3, 3, 2), errorRatio = 0.914600
● 画图(1,3,1),线性 / 非线性
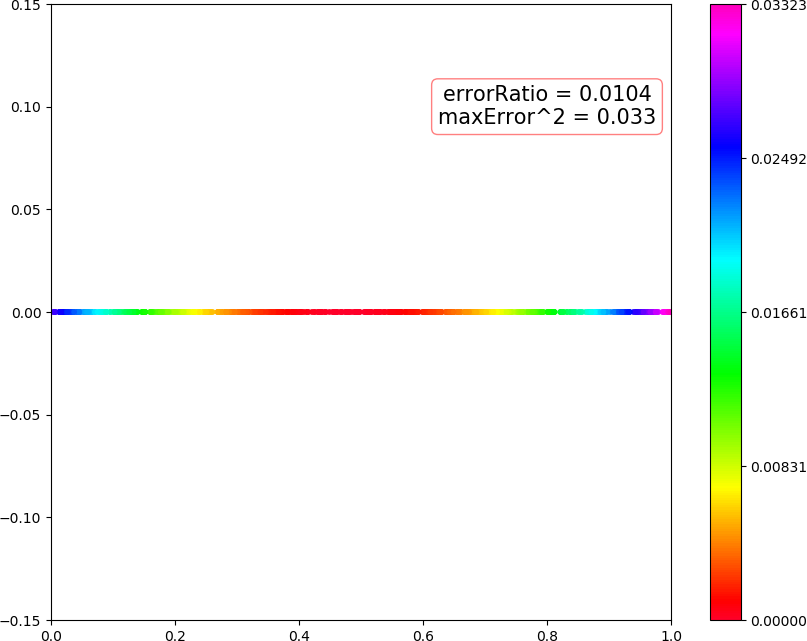

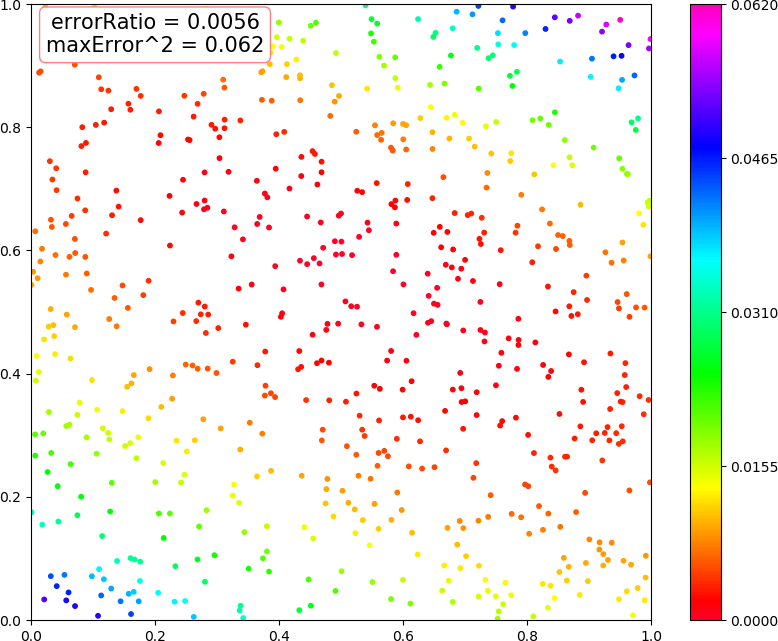
● 画图 (2,3,2) 线性,(2,3,2) 非线性,(2,10,2) 非线性,画图 (2,4,3,2) 非线性
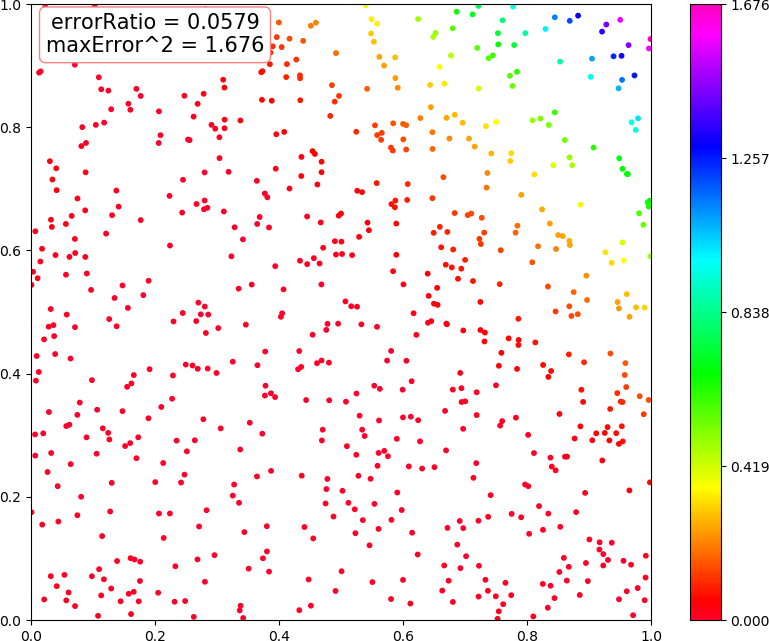
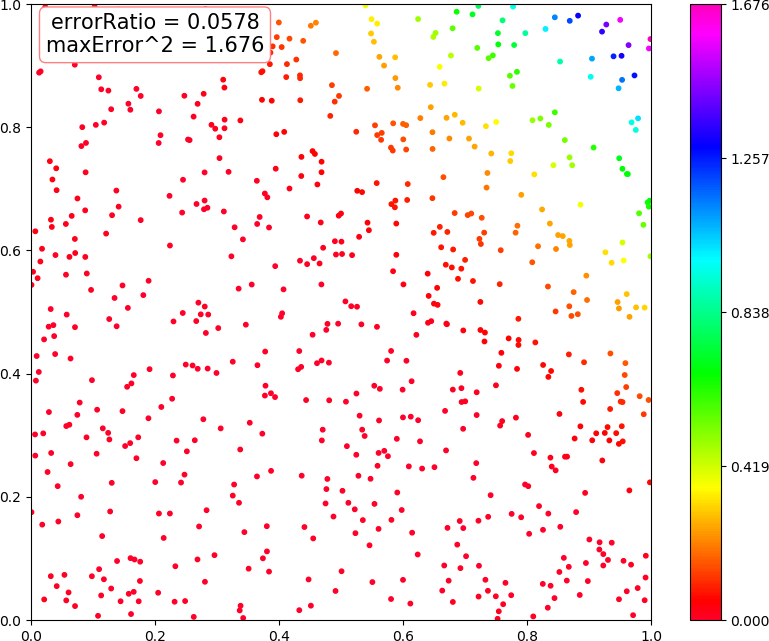

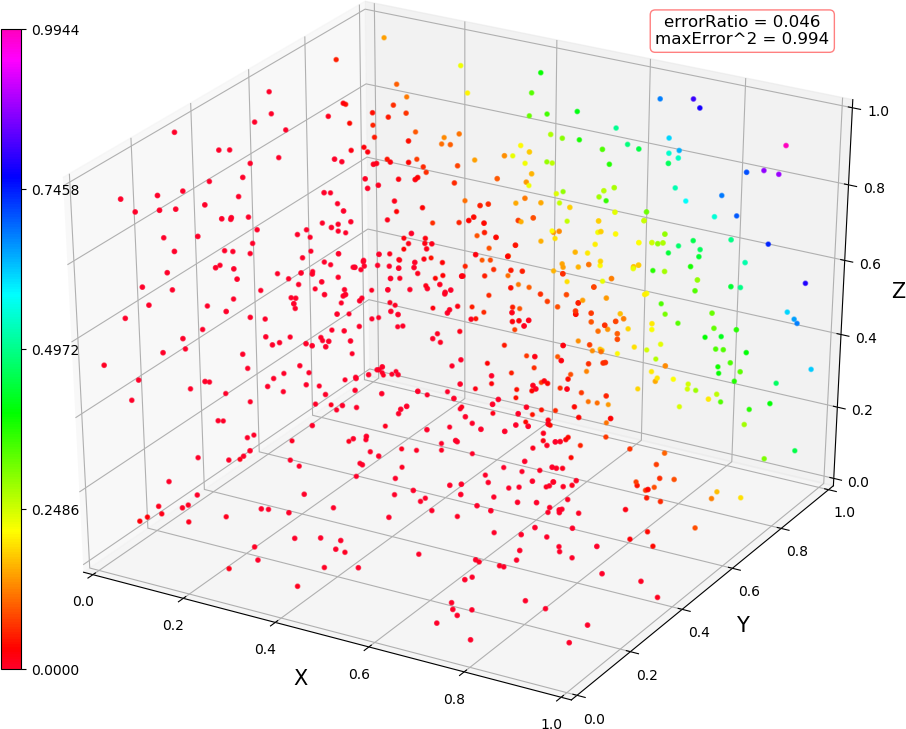
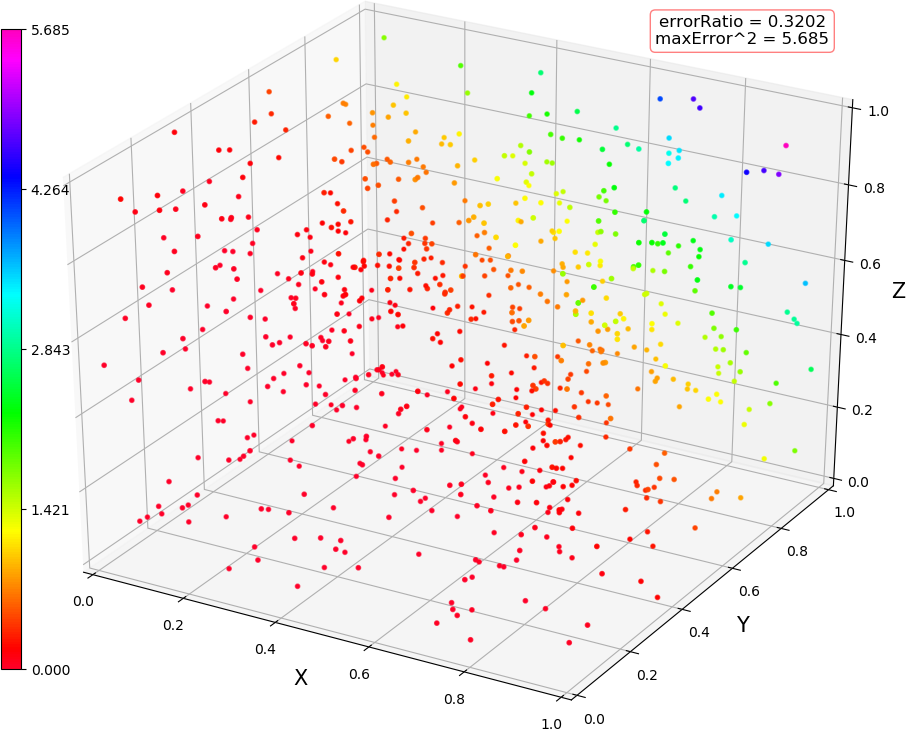
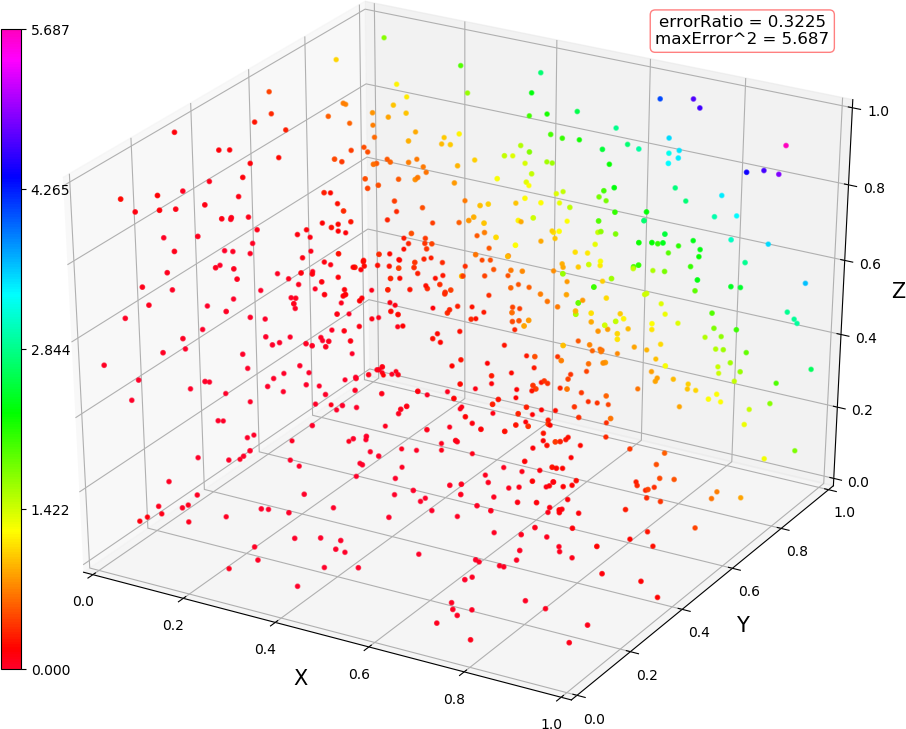
● 画图 (3,3,2) 线性,(3,3,2) 非线性,(3,10,2) 线性,(3,10,2) 非线性

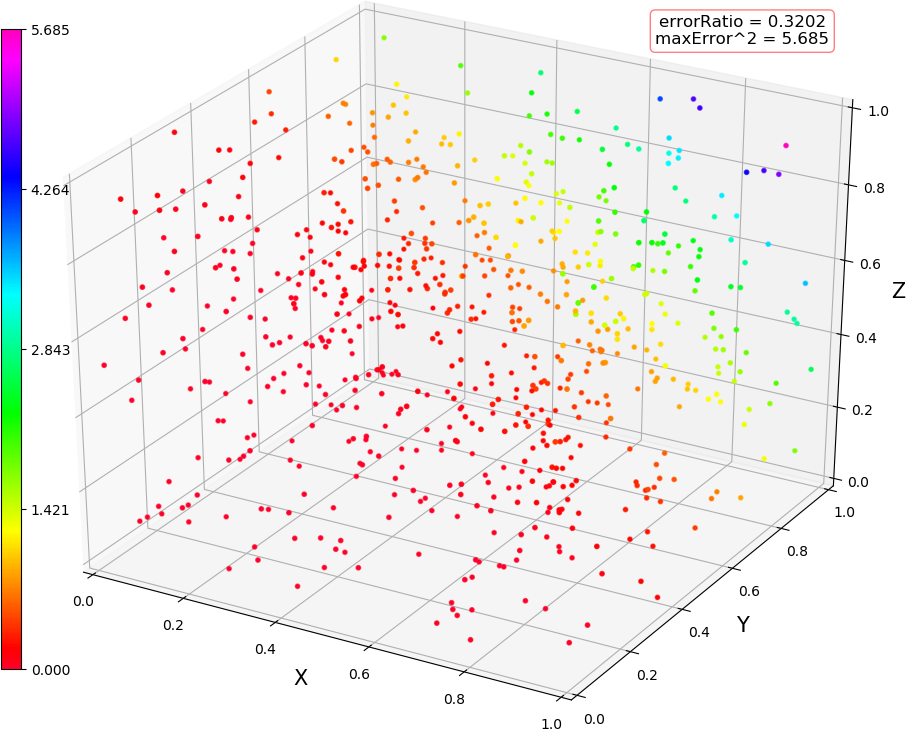
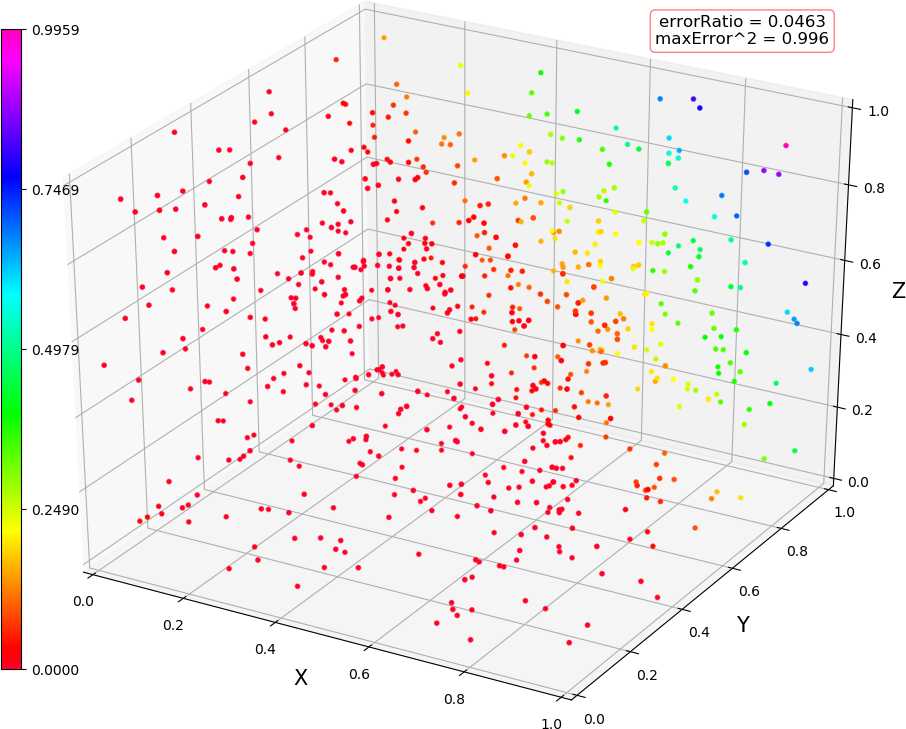
● 画图 (3,4,3,2) 线性,(3,4,3,2) 非线性
● 留坑,采用查分方法作各神经元的梯度检查