算法复杂度

一、概念

算法的效率主要由时间复杂度和空间复杂度来评估

时间复杂度：评估执行程序所需的时间，可以估算出程序对处理器的使用程度

空间复杂度：评估执行程序所需的存储空间，可以估算出程序对计算机内存的使用程度

设计算法时，时间复杂度比空间复杂度更容易出问题，所以一般情况下只对时间复杂度进行研究，一般算法的复杂度就是指时间复杂度

用O(n)来体现算法时间复杂度的记法被称作大O表示法

二、推导方法

1、用常数1取代运行时间中的所有加法常数

2、只保留最高阶项

3、去除最高阶的常数

三、时间复杂度量级示例和比较

1、常数阶 O(1)

i = 1, j = 2
return i + j

语句只执行1次，哈希算法就是典型的O(1)

2、对数阶 O(logn)

i = 1
for(i < n) {
    i = i * 2  
}

可以看到n不停增加对循环次数的影响较小，小于线性阶，例：二分查找法

3、线性阶 O(n)

i = 1
for(i < n) {
    i = i + 1
}

循环了n次，时间复杂度随着n的增加线性增加，遍历算法

4、线性对数阶 O(nlogn)

j = 1
for(j < n) {
    i = 1
    for(i < n) {
        i = i * 2
    }
}

O(n) * O(logn) = O(nlogn)，比如当n增大256倍时，时间复杂度为原先的256*8倍，例：归并排序法

5、平方阶 O(n²)

i = 1
for(i < n) {
    i = 1
    for(j < n) {
        O(1)
    }
}

O(n) * O(n) = O(n²)，例：冒泡排序

6、立方阶 O(n³)

同理O(n) * O(n) * O(n) = O(n3)

7、k次方阶 O(n^k)

同理

8、指数阶 O(2ⁿ)

fun(n) {
    if(n <= 1) {
        return 2;
    } else {
        return fun(n - 1) + fun(n - 2)
    }
}

几何倍增序列说的就是它，参考国王放米粒的故事，1、2、4、8、16.... 增长下去时间复杂度飙升

9、阶乘阶 O(n!)

fun(n) {
    if(n <= 1) {
        return 1
    else {
        return n * fun(n - 1)
    }
}

1*2*3*4*....*(n-2)*(n-1)*n，比指数阶增长的还快

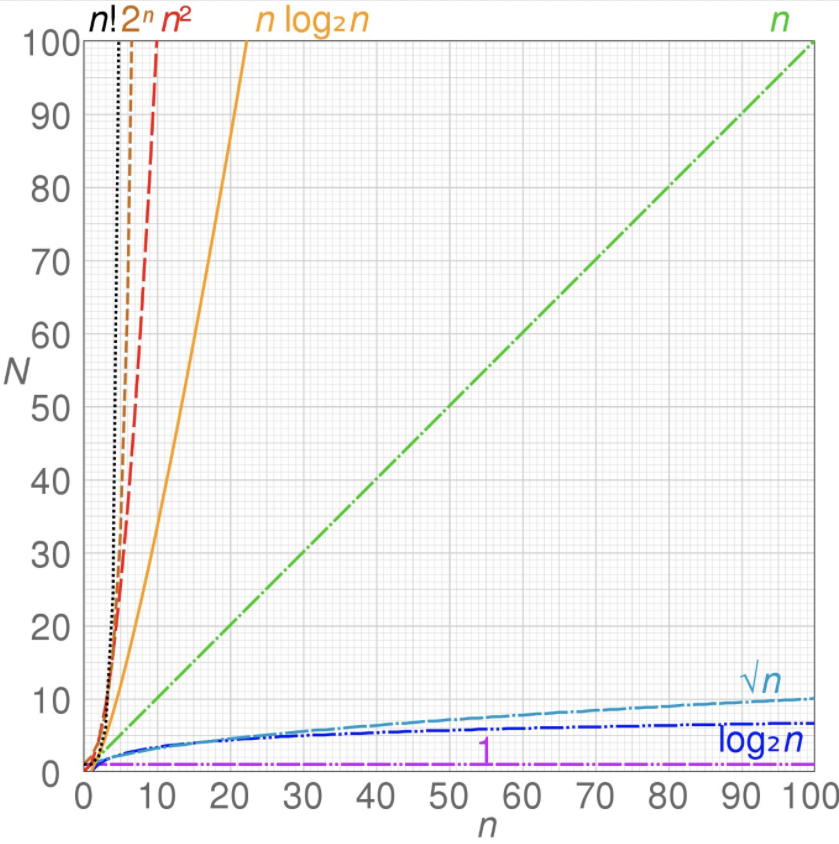
10、复杂度比较

O(1) < O(logn) < O(n) < O(nlogn) < O(n²) < O(n³) < O(n^k) < O(2ⁿ) < O(n!)

四、空间复杂度

也叫渐进空间复杂度，概念和时间复杂度类似，表示数据规模和存储空间的增长关系

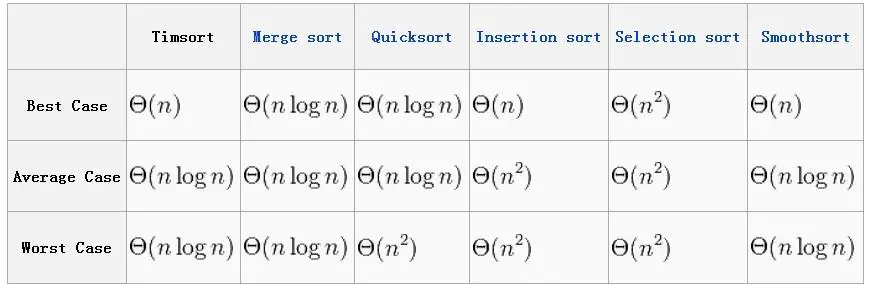
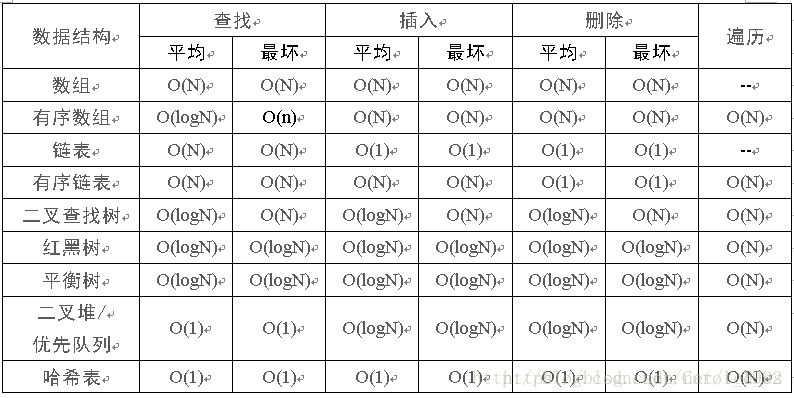
五、复杂度对比

 

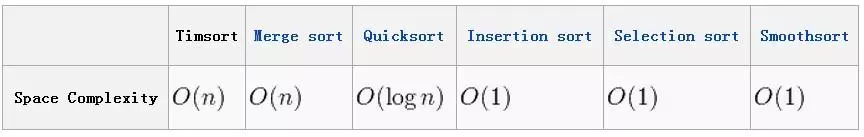
六、几个链接

详细的算法可视化分析（可以用浏览器翻译一下）：https://bost.ocks.org/mike/algorithms

常见排序可视化：https://www.cnblogs.com/liululin/p/5897059.html、https://visualgo.net/zh、https://www.ee.ryerson.ca/~courses/coe428/sorting/sorting.html

jdk1.7从python引入的排序算法Timsort说明：https://www.jianshu.com/p/892ebd063ad9