和某atcoder题的idea很像。
转化比较巧妙。
把两种学校的课程作为两维。
把平面划分成((n+2)*(m+2))个矩形。
把(x,y)作前缀和。
如果(x)有一个值(a),则画一条(x=a)的线。
如果(y)有一个值(b),则画一条(y=b)的线。
然后我们就要在这些直线的交点上选择一个矩形,使得周长最大。
(其实我本来也想到把两种学校的课程作为两维的,但是以为是错的)
相同元素不能选相当于平面上有一些障碍。矩形不能包含障碍。
借用官方题解的一张图:
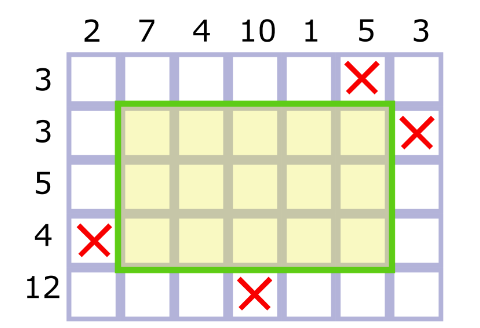
考虑分治。如果我们取一条处在中间的直线(l),计算过(l)的方案。
考虑枚举矩形的底边。则随着顶边的向上移动,矩形能够取的左/右边界会一直向内缩。
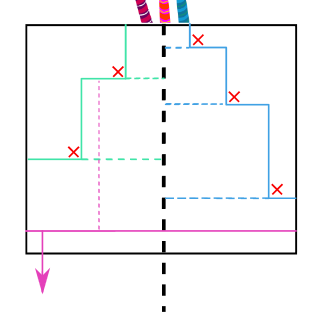
可以使用单调栈+线段树区间加法。
时间复杂度(O(nlog_2^2n))
实际上我们只需要分治一次,因为最优方案一定过中线。
如果我们不选择一个序列的元素,另一个序列的元素可以全选,答案至少为(max(sum x,sum y))
所以我们一定会选择中线。
时间复杂度(O(nlog_2n))