计算几何 学习笔记

部分参考oi-wiki
注：本文中的所有代码都不保证正确性
以下知识需要高中必修4作铺垫
判定一个整数是正数还是负数：
由于精度问题，设eps。eps是一个较小的数。
点的表示：使用一个结构体((x,y))表示(x,y)坐标

struct pt{
	int x,y;
};

向量的表示：使用一个结构体((x,y))表示向量的坐标式(overrightarrow{A}=(x,y))
代码实现可以这样：

typedef vc pt;

运算法则：
点+向量=点
点-向量=点
向量+向量=向量
向量-向量=向量
向量*数量=向量（点乘）

pt operator +(pt x,vc y){
	return (pt){x.x+y.x,x.y+y.y};
}
pt operator -(pt x,vc y){
	return (pt){x.x-y.x,x.y-y.y};
}
vc operator +(vc x,vc y){
	return (vc){x.x+y.x,x.y+y.y};
}
vc operator -(vc x,vc y){
	return (vc){x.x-y.x,x.y-y.y};
}
vc operator *(vc x,double y){
	return (vc){x.x*y,x.y*y};
}
vc operator /(vc x,double y){
	return (vc){x.x/y,x.y/y};
}

向量的模：

double di(pt x){
	return sqrt(x.x*x.x+x.y*x.y);
}

点积式
向量((x,y)cdot(a,b)=x*a+y*b)
如果((x,y)=overrightarrow{A},(z,a)=overrightarrow{B})
则(overrightarrow{A}cdotoverrightarrow{B}=|A|cdot|B|cdotcos<A,B>)
叉积式：
向量((x,y)cdot(a,b)=x*b-y*a)
如果((x,y)=overrightarrow{A},(z,a)=overrightarrow{B})
则(overrightarrow{A} imesoverrightarrow{B}=|A|cdot|B|cdotsin<A,B>)
根据平面向量基本定理：
如果有两个向量（基底）(a,b)
存在唯一一对整数(x,y)使得(ax+by=c)
如果设基底为((1,0)=x,(0,1)=y)
则每个向量可以被分解为(ax+by=c)
数量积(overrightarrow{A}cdotoverrightarrow{B}=|A|cdot|B|cdotcos<A,B>=(ax+by)cdot (cx+dy)=axcdot cx+axcdot dy+bycdot cx+bycdot dy=ac+bd)
向量积(overrightarrow{A} imes overrightarrow{B}=|A|cdot|B|cdotsin<A,B>=(ax+by)cdot (cx+dy)=axcdot cx+axcdot dy+bycdot cx+bycdot dy=ad-bc)

int dt(vc x,vc y){
	return x.x*y.x+x.y*y.y;
}
int cr(vc x,vc y){
	return x.x*y.y-x.y*y.x;
}

点积可以用于判定垂直，也可用于求两个向量的夹角。
(cfrac{overrightarrow{A}cdotoverrightarrow{B}}{|A|cdot|B|}=cos<A,B>)
当(Aperp B,cos<A,B>=0)
(overrightarrow{A}cdotoverrightarrow{B}=|A|cdot|B|cdotcos<A,B>=0)
叉积可以用于判定平行，还可以用于求出三角形的有向面积。
三角形面积公式(absin(angle{ab}))，所以叉积可以用于求有向面积。
(cfrac{overrightarrow{A}cdotoverrightarrow{B}}{|A|cdot|B|}=cos<A,B>)
当(Aparallel B,sin<A,B>=sin(90^{circ}))
(overrightarrow{A} imesoverrightarrow{B}=|A|cdot|B|cdotsin<A,B>=0)

db ag(vc x,vc y){
	return acos(dt(a,b)/di(a)/di(b));
}

求一个向量的法向量：
如果向量的坐标式为((x,y))，则((-y,x))与该向量垂直，除以模就是法向量。

vc qf(vc x){
	db v=di(x);
	return (vc){-x.y/v,x.x/v};
}

向量的旋转：
根据平面向量基本定理，以((1,0),(0,1))为基底，有唯一的方式表示出要旋转的向量((x,y)=(1,0)*x+(0,1)*y)
分别旋转两个向量再加起来，得到(x*(cos heta,sin heta)+y*(-sin heta,cos heta))

vc rot(vc x,double y){
	db v1=sin(y),v2=cos(y);
	return (vc){x.x*v2-y.x*v1,x.x*v1+x.y*v2};
}

点到直线的距离
利用叉积求出面积，得到了两个向量构成的有向平行四边形的距离。
然后除以平行四边形的底边长，得到平行四边形的高再绝对值即点到直线的距离
现在要求的是(p)到(a,b)连成的直线的距离。

double di(pt p,pt a,pt b){
	vc v1=p-a,v2=b-a;
	return fabs(cr(v1,v2))/di(v2);
}

点到线段的距离
和上一问不同的是，这道题不能直接作直线的垂直。
如果作垂直，可能不在线段上。
解决方法是：当平行四边形的高在区域外，答案取到两个端点的距离的最小值。
假设(overrightarrow{b}-overrightarrow{a}=v1,overrightarrow{p}-overrightarrow{a}=v2,overrightarrow{p}-overrightarrow{b}=v3)
当(v2)和(v1)的夹角>90度时，则p的投影在直线外面
同理，当(v3,v1)的夹角<90度时，则p的投影也在直线外面。
使用这个结论判定即可。

double dts(pl p,pl a,pl b){
	if(a==b)return di(p-a);
	vc v1=b-a,v2=p-a,v3=p-b;
	if(dc(dt(v1,v2))<0)return di(v2);
	else if(dc(dt(v1,v3))>0)return di(v3);
	return fabs(cr(v1,v2))/di(v1); 
}

如果线段(ab)和(cd)相交，那么(a,b)到直线(cd)作垂线有交点，或者(c,d)到直线(ab)作垂线有交点
使用刚才求点到线段的距离的方法判定即可。

判定两个线段是否相交
快速跨立实验：判定一条线段的两个点是否在另外一条线段的两边。
要做2次。

bool xj(pt a,pt b,pt c,pt d){
	double v1=cr(b-a,c-a),v2=cr(b-a,d-a),v3=cr(d-c,a-c),v4=cr(d-c,b-c);
	return dc(v1)*dc(v2)<0&&dc(v3)*dc(v4)<0;
}

求一个点是否在多边形上可以使用角度/射线法。
具体可以看uoj白鸽。
求两条直线的交点：

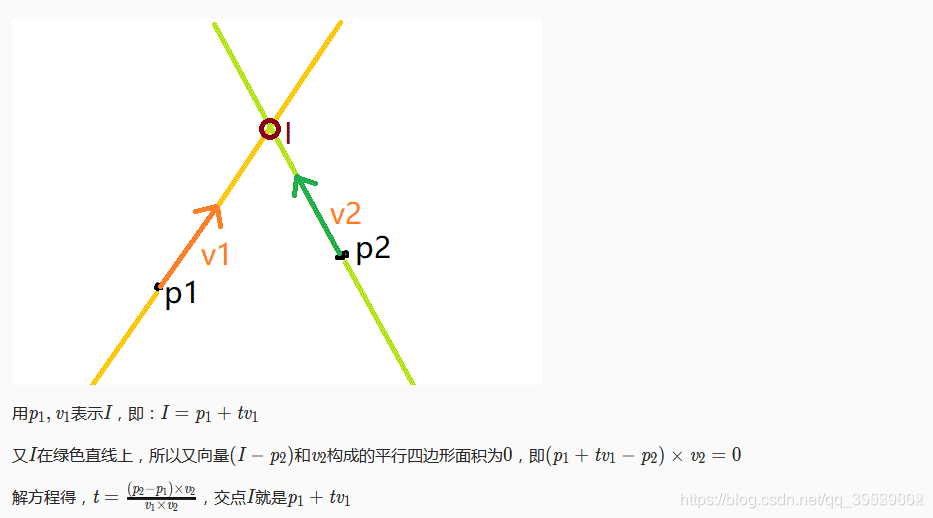
盗了图。

pt its(pt p,vc v,pt q,vc w){
	vc t=p-q;
	double g=cr(w,t)/cr(v,w);
	return p+v*g;
}

求两条线段的交点只需要先判定是否相交，再求两条直线的交点即可。
求一个多边形的面积可以三角剖分，对每个三角形的有向面积加起来最后再/2。
这样子做，外边的部分恰好被抵消了。
最后要取绝对值。

double ar(pt *a,int n){
	double ans=0;
	for(int i=1;i<n-1;i++)
		ans+=cr(a[i]-a[0],a[i+1]-a[0]);
	return ans/2;
}

凸包
求出点集的凸包可以使用如下方法：
先把所有点按照(x)值排序
维护一个上凸包和一个下凸包。
上凸包的求法：把1~n的所有点按顺序插入凸包。
使用一个栈维护现在的凸包。
下凸包的求法：把1~n-1的所有点逆序插入凸包。
使用一个栈维护现在的凸包。
最终把这两个凸包合起来，删除最后一个点就是最终的凸包。

void tb(pt *a,int b,pl *b){
	sort(a+1,a+n+1);
	int tp=0;
	if(n==1){
		b[++tp]=1;
		return;
	}
	tp=1;
	for(int i=1;i<=n;i++){
		while(n>2&&dc(cr(b[tp-1]-b[tp-2],a[i]-b[tp-2]))<=0)tp--;
		b[tp++]=a[i];
	}
	int v=tp;
	for(int i=n-1;i;i--){
		while(tp>v&&dc(cr(b[tp-1]-b[tp-2],a[i]-b[tp-2]))<=0)tp--;
		b[tp++]=a[i];
	}
	tp--;
}

完整代码：

#include<bits/stdc++.h>
using namespace std;
#define eps 1e-8
struct pt{
	double x,y;
};
int dc(double x){
	if(fabs(x)<eps)return 0;
	return 1;
}
typedef vc pt;
pt operator +(pt x,vc y){
	return (pt){x.x+y.x,x.y+y.y};
}
pt operator -(pt x,vc y){
	return (pt){x.x-y.x,x.y-y.y};
}
vc operator +(vc x,vc y){
	return (vc){x.x+y.x,x.y+y.y};
}
vc operator -(vc x,vc y){
	return (vc){x.x-y.x,x.y-y.y};
}
vc operator *(vc x,double y){
	return (vc){x.x*y,x.y*y};
}
vc operator /(vc x,double y){
	return (vc){x.x/y,x.y/y};
}
vc operator ==(vc x,vc y){
	return x.x==y.x&&x.y==y.y;
}
pt operator ==(pt x,pt y){
	return x.x==y.x&&x.y==y.y;
}
double di(pt x){
	return sqrt(x.x*x.x+x.y*x.y);
}
int dt(vc x,vc y){
	return x.x*y.x+x.y*y.y;
}
int cr(vc x,vc y){
	return x.x*y.y-x.y*y.x;
}
db ag(vc x,vc y){
	return acos(dt(a,b)/di(a)/di(b));
}
vc qf(vc x){
	db v=di(x);
	return (vc){-x.y/v,x.x/v};
}
vc rot(vc x,double y){
	db v1=sin(y),v2=cos(y);
	return (vc){x.x*v2-y.x*v1,x.x*v1+x.y*v2};
}
double dtl(pt p,pt a,pt b){
	vc v1=p-a,v2=b-a;
	return fabs(cr(v1,v2))/di(v2);
}
double dts(pl p,pl a,pl b){
	if(a==b)return di(p-a);
	vc v1=b-a,v2=p-a,v3=p-b;
	if(dc(dt(v1,v2))<0)return di(v2);
	else if(dc(dt(v1,v3))>0)return di(v3);
	return fabs(cr(v1,v2))/di(v1); 
}
bool xj(pt a,pt b,pt c,pt d){
	double v1=cr(b-a,c-a),v2=cr(b-a,d-a),v3=cr(d-c,a-c),v4=cr(d-c,b-c);
	return dc(v1)*dc(v2)<0&&dc(v3)*dc(v4)<0;
}
pt its(pt p,vc v,pt q,vc w){
	vc t=p-q;
	double g=cr(w,t)/cr(v,w);
	return p+v*g;
}
double ar(pt *a,int n){
	double ans=0;
	for(int i=1;i<n-1;i++)
		ans+=cr(a[i]-a[0],a[i+1]-a[0]);
	return ans/2;
}
void tb(pt *a,int b,pl *b){
	sort(a+1,a+n+1);
	int tp=0;
	if(n==1){
		b[++tp]=1;
		return;
	}
	tp=1;
	for(int i=1;i<=n;i++){
		while(n>2&&dc(cr(b[tp-1]-b[tp-2],a[i]-b[tp-2]))<=0)tp--;
		b[tp++]=a[i];
	}
	int v=tp;
	for(int i=n-1;i;i--){
		while(tp>v&&dc(cr(b[tp-1]-b[tp-2],a[i]-b[tp-2]))<=0)tp--;
		b[tp++]=a[i];
	}
	tp--;
}

未完待续