The Power of Xiangqi
Time Limit: 2000/1000 MS (Java/Others) Memory Limit: 32768/32768 K (Java/Others)
Total Submission(s): 284 Accepted Submission(s): 145
Problem Description
Xiangqi is one of the most popular two-player board games in China. The game represents a battle between two armies with the goal of capturing the enemy’s “general” piece.
Now we introduce some basic rules of Xiangqi. Xiangqi is played on a 10×9 board and the pieces are placed on the intersections (points). There are two groups of pieces marked by black or red Chinese characters, belonging to the two players separately. During the game, each player in turn moves one piece from the point it occupies to another point. No two pieces can occupy the same point at the same time. A piece can be moved onto a point occupied by an enemy piece, in which case the enemy piece is "captured" and removed from the board. When the general is in danger of being captured by the enemy player on the enemy player’s next move, the enemy player is said to have "delivered a check". If the general's player can make no move to prevent the general's capture by next enemy move, the situation is called “checkmate”.
Each player has 7 kinds of pieces in this game. Their names, offense power and symbol letters are shown in the table below:
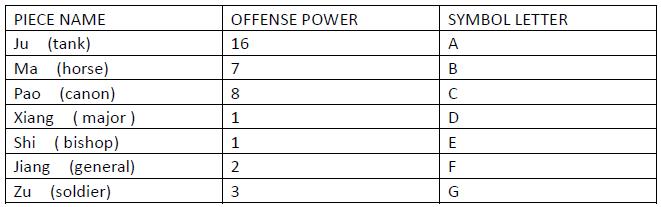
Now show you the pieces of red player and black player, you are going to find out which player has the larger total offense power. Since Ma and Pao working together can have good effect, if a player has no Ma or no Pao, or has neither, his total offense power will be decreased by one. But the total offense power can't be decreased to zero, it is at least one.
Input
The first line is an integer T ( T <= 20) meaning there are T test cases.
For each test case: The first line shows which pieces the red player has. It begins with an integer n ( 0 < n <= 16) meaning the number of pieces.
Then n letters follows, all separated by one or more blanks. Each letter is a symbol letter standing for a piece, as shown in the table above.
The second line describes the situation of the black player, in the same format as the first line.
For each test case: The first line shows which pieces the red player has. It begins with an integer n ( 0 < n <= 16) meaning the number of pieces.
Then n letters follows, all separated by one or more blanks. Each letter is a symbol letter standing for a piece, as shown in the table above.
The second line describes the situation of the black player, in the same format as the first line.
Output
For each test case, if the red player has more offense power, then print "red". If the black player has more offense power, then print "black". If there is a tie, print "tie".
Sample Input
3
2 A B
2 A B
7 A A B C D D F
7 A A B B C C F
5 A A B B F
3 A B F
Sample Output
tie
black
red
Source
Statistic | Submit | Discuss | Note
1 #include <iostream> 2 #include <fstream> 3 #include <string> 4 #include <cstdio> 5 #include <cmath> 6 #include <cstring> 7 #include <algorithm> 8 #include <map> 9 #include <vector> 10 #include <queue> 11 #include <stack> 12 #define LL long long 13 #define MAXI 2147483647 14 #define MAXL 9223372036854775807 15 #define eps (1e-8) 16 #define dg(i) cout << "*" << i << endl; 17 18 using namespace std; 19 20 int main() 21 { 22 const int power[7] = {16, 7, 8, 1, 1, 2, 3}; 23 int T, n, R, B; 24 char c; 25 bool ma, pao; 26 scanf("%d", &T); 27 while(T--) 28 { 29 R = B = 0; 30 scanf("%d", &n); 31 ma = pao = 0; 32 while(n--) 33 { 34 cin >> c; 35 R += power[c - 'A']; 36 if(c == 'C') pao = 1; 37 else if(c == 'B') ma = 1; 38 } 39 if(pao + ma != 2 && R > 1) R--; 40 scanf("%d", &n); 41 ma = pao = 0; 42 while(n--) 43 { 44 cin >> c; 45 B += power[c - 'A']; 46 if(c == 'C') pao = 1; 47 else if(c == 'B') ma = 1; 48 } 49 if(pao + ma != 2 && B > 1) B--; 50 if(B > R) puts("black"); 51 else if(B == R) puts("tie"); 52 else puts("red"); 53 } 54 return 0; 55 }