pageRank算法（Java)

参考：http://blog.codinglabs.org/articles/intro-to-pagerank.html

当然，实际上现在的搜索引擎都是有分词机制的，例如如果以“张洋的博客”为关键词，搜索引擎会自动将其分解为“张洋 的 博客”三个词，而“的”作为停止词（Stop Word）会被过滤掉。关于分词及词权评价算法（如TF-IDF算法）是一个很大的话题，这里就不展开讨论了，为了简单此处可以将搜索引擎想象为一个只会机械匹配词语的检索系统。

这样看来，建立一个搜索引擎的核心问题就是两个：1、建立资料库；2、建立一种数据结构，可以根据关键词找到含有这个词的页面。

第一个问题一般是通过一种叫爬虫（Spider）的特殊程序实现的（当然，专业领域搜索引擎例如某个学术会议的论文检索系统可能直接从数据库建立资料库），简单来说，爬虫就是从一个页面出发（例如新浪首页），通过HTTP协议通信获取这个页面的所有内容，把这个页面url和内容记录下来（记录到资料库），然后分析页面中的链接，再去分别获取这些链接链向页面的内容，记录到资料库后再分析这个页面的链接……重复这个过程，就可以将整个互联网的页面全部获取下来（当然这是理想情况，要求整个Web是一个强连通（Strongly Connected），并且所有页面的robots协议允许爬虫抓取页面，为了简单，我们仍然假设Web是一个强连通图，且不考虑robots协议）。抽象来看，可以将资料库看做一个巨大的key-value结构，key是页面url，value是页面内容。

第二个问题是通过一种叫倒排索引（inverted index）的数据结构实现的，抽象来说倒排索引也是一组key-value结构，key是关键词，value是一个页面编号集合（假设资料库中每个页面有唯一编号），表示这些页面含有这个关键词。本文不详细讨论倒排索引的建立方法。

有了上面的分析，就可以简要说明搜索引擎的核心动作了：搜索引擎获取“张洋 博客”查询条件，将其分为“张洋”和“博客”两个词。然后分别从倒排索引中找到“张洋”所对应的集合，假设是{1， 3， 6， 8， 11， 15}；“博客”对应的集合是{1， 6， 10， 11， 12， 17， 20， 22}，将两个集合做交运算（intersection），结果是{1， 6， 11}。最后，从资料库中找出1、6、11对应的页面返回给用户就可以了。

上面阐述了一个非常简单的搜索引擎工作框架，虽然现代搜索引擎的具体细节原理要复杂的多，但其本质却与这个简单的模型并无二异。实际Google在上述两点上相比其前辈并无高明之处。其最大的成功是解决了第三个、也是最为困难的问题：如何对查询结果排序。

我们知道Web页面数量非常巨大，所以一个检索的结果条目数量也非常多，例如上面“张洋 博客”的检索返回了超过260万条结果。用户不可能从如此众多的结果中一一查找对自己有用的信息，所以，一个好的搜索引擎必须想办法将“质量”较高的页面排在前面。其实直观上也可以感觉出，在使用搜索引擎时，我们并不太关心页面是否够全（上百万的结果，全不全有什么区别？而且实际上搜索引擎都是取top，并不会真的返回全部结果。），而很关心前一两页是否都是质量较高的页面，是否能满足我们的实际需求。

因此，对搜索结果按重要性合理的排序就成为搜索引擎的最大核心，也是Google最终成功的突破点

早期搜索引擎的做法

不评价

这个看起来可能有点搞笑，但实际上早期很多搜索引擎（甚至包括现在的很多专业领域搜索引擎）根本不评价结果重要性，而是直接按照某自然顺序（例如时间顺序或编号顺序）返回结果。这在结果集比较少的情况下还说得过去，但是一旦结果集变大，用户叫苦不迭，试想让你从几万条质量参差不齐的页面中寻找需要的内容，简直就是一场灾难，这也注定这种方法不可能用于现代的通用搜索引擎。

基于检索词的评价

后来，一些搜索引擎引入了基于检索关键词去评价搜索结构重要性的方法，实际上，这类方法如TF-IDF算法在现代搜索引擎中仍在使用，但其已经不是评价质量的唯一指标。完整描述TF-IDF比较繁琐，本文这里用一种更简单的抽象模型描述这种方法。

基于检索词评价的思想非常朴素：和检索词匹配度越高的页面重要性越高。“匹配度”就是要定义的具体度量。一个最直接的想法是关键词出现次数越多的页面匹配度越高。还是搜索“张洋 博客”的例子：假设A页面出现“张洋”5次，“博客”10次；B页面出现“张洋”2次，“博客”8次。于是A页面的匹配度为5 + 10 = 15，B页面为2 + 8 = 10，于是认为A页面的重要性高于B页面。很多朋友可能意识到这里的不合理性：内容较长的网页往往更可能比内容较短的网页关键词出现的次数多。因此，我们可以修改一下算法，用关键词出现次数除以页面总词数，也就是通过关键词占比作为匹配度，这样可以克服上面提到的不合理。

早期一些搜索引擎确实是基于类似的算法评价网页重要性的。这种评价算法看似依据充分、实现直观简单，但却非常容易受到一种叫“Term Spam”的攻击。

Term Spam

其实从搜索引擎出现的那天起，spammer和搜索引擎反作弊的斗法就没有停止过。Spammer是这样一群人——试图通过搜索引擎算法的漏洞来提高目标页面（通常是一些广告页面或垃圾页面）的重要性，使目标页面在搜索结果中排名靠前。

现在假设Google单纯使用关键词占比评价页面重要性，而我想让我的博客在搜索结果中排名更靠前（最好排第一）。那么我可以这么做：在页面中加入一个隐藏的html元素（例如一个div），然后其内容是“张洋”重复一万次。这样，搜索引擎在计算“张洋 博客”的搜索结果时，我的博客关键词占比就会非常大，从而做到排名靠前的效果。更进一步，我甚至可以干扰别的关键词搜索结果，例如我知道现在欧洲杯很火热，我就在我博客的隐藏div里加一万个“欧洲杯”，当有用户搜索欧洲杯时，我的博客就能出现在搜索结果较靠前的位置。这种行为就叫做“Term Spam”。

早期搜索引擎深受这种作弊方法的困扰，加之基于关键词的评价算法本身也不甚合理，因此经常是搜出一堆质量低下的结果，用户体验大大打了折扣。而Google正是在这种背景下，提出了PageRank算法，并申请了专利保护。此举充分保护了当时相对弱小Google，也使得Google一举成为全球首屈一指的搜索引擎。

PageRank算法

上文已经说到，PageRank的作用是评价网页的重要性，以此作为搜索结果的排序重要依据之一。实际中，为了抵御spam，各个搜索引擎的具体排名算法是保密的，PageRank的具体计算方法也不尽相同，本节介绍一种最简单的基于页面链接属性的PageRank算法。这个算法虽然简单，却能揭示PageRank的本质，实际上目前各大搜索引擎在计算PageRank时链接属性确实是重要度量指标之一。

简单PageRank计算

首先，我们将Web做如下抽象：1、将每个网页抽象成一个节点；2、如果一个页面A有链接直接链向B，则存在一条有向边从A到B（多个相同链接不重复计算边）。因此，整个Web被抽象为一张有向图。

现在假设世界上只有四张网页：A、B、C、D，其抽象结构如下图：

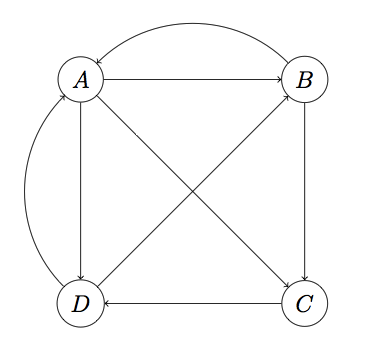
显然这个图是强连通的（从任一节点出发都可以到达另外任何一个节点）。

然后需要用一种合适的数据结构表示页面间的连接关系。其实，PageRank算法是基于这样一种背景思想：被用户访问越多的网页更可能质量越高，而用户在浏览网页时主要通过超链接进行页面跳转，因此我们需要通过分析超链接组成的拓扑结构来推算每个网页被访问频率的高低。最简单的，我们可以假设当一个用户停留在某页面时，跳转到页面上每个被链页面的概率是相同的。例如，上图中A页面链向B、C、D，所以一个用户从A跳转到B、C、D的概率各为1/3。设一共有N个网页，则可以组织这样一个N维矩阵：其中i行j列的值表示用户从页面j转到页面i的概率。这样一个矩阵叫做转移矩阵（Transition Matrix）。下面的转移矩阵M对应上图：

然后，设初始时每个页面的rank值为1/N，这里就是1/4。按A-D顺序将页面rank为向量v：

注意，M第一行分别是A、B、C和D转移到页面A的概率，而v的第一列分别是A、B、C和D当前的rank，因此用M的第一行乘以v的第一列，所得结果就是页面A最新rank的合理估计，同理，Mv的结果就分别代表A、B、C、D新rank：

然后用M再乘以这个新的rank向量，又会产生一个更新的rank向量。迭代这个过程，可以证明v最终会收敛，即v约等于Mv，此时计算停止。最终的v就是各个页面的pagerank值。例如上面的向量经过几步迭代后，大约收敛在（1/4, 1/4, 1/5, 1/4），这就是A、B、C、D最后的pagerank。

处理Dead Ends

上面的PageRank计算方法假设Web是强连通的，但实际上，Web并不是强连通（甚至不是联通的）。下面看看PageRank算法如何处理一种叫做Dead Ends的情况。

所谓Dead Ends，就是这样一类节点：它们不存在外链。看下面的图：

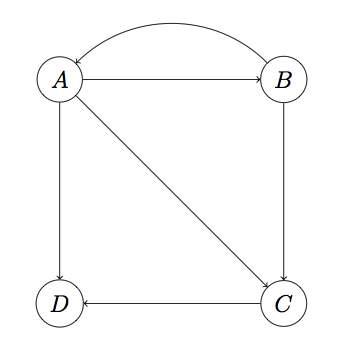
注意这里D页面不存在外链，是一个Dead End。上面的算法之所以能成功收敛到非零值，很大程度依赖转移矩阵这样一个性质：每列的加和为1。而在这个图中，M第四列将全为0。在没有Dead Ends的情况下，每次迭代后向量v各项的和始终保持为1，而有了Dead Ends，迭代结果将最终归零（要解释为什么会这样，需要一些矩阵论的知识，比较枯燥，此处略）。

处理Dead Ends的方法如下：迭代拿掉图中的Dead Ends节点及Dead Ends节点相关的边（之所以迭代拿掉是因为当目前的Dead Ends被拿掉后，可能会出现一批新的Dead Ends），直到图中没有Dead Ends。对剩下部分计算rank，然后以拿掉Dead Ends逆向顺序反推Dead Ends的rank。

以上图为例，首先拿到D和D相关的边，D被拿到后，C就变成了一个新的Dead Ends，于是拿掉C，最终只剩A、B。此时可很容易算出A、B的PageRank均为1/2。然后我们需要反推Dead Ends的rank，最后被拿掉的是C，可以看到C前置节点有A和B，而A和B的出度分别为3和2，因此C的rank为：1/2 * 1/3 + 1/2 * 1/2 = 5/12；最后，D的rank为：1/2 * 1/3 + 5/12 * 1 = 7/12。所以最终的PageRank为（1/2, 1/2, 5/12, 7/12）。

代码按照《《搜索引擎信息检索实践》》中的的伪码书写

package com.bupt.acm;

import java.util.Scanner;

/**
 * PageRank算法
 * 本文算法是通过邻接矩阵表示图，而不是邻接表
 * @author DELL
 * 
 */
public class Main37 {

    private final static int ITTIME=10;
    public static void main(String[] args) {
        Scanner scanner = new Scanner(System.in);
        int m;
        int[][] numb;
        System.out.println("开始....输入N");
        while (scanner.hasNext()) {
            m = scanner.nextInt();
            numb = new int[m][m];
            for (int i = 0; i < m; i++) {
                //System.out.println("输入行值：");
                for (int j = 0; j < m; j++) {
                    numb[i][j] = scanner.nextInt();
                }
            }
            // 声明当前PageRank估值
            double[] nowRank = new double[m];
            // 声明最终估计的结果
            double[] resultRank = new double[m];
            for (int i = 0; i < m; i++)
                nowRank[i] = 1.0 / m;
            boolean flag = true;// 表示当前最终网页链接估计收敛
            double r = 0.15;// 考虑其他可能0 1 0 1 0 0 1 0 0 0 0 1 1 0 0 0
            int sum=0;//表示迭代次数；
            while (flag) {
                if(sum==Main37.ITTIME)
                    break;
                sum++;
                System.out.println("第"+sum+"轮迭代开始----");
                for (int i = 0; i < m; i++)
                    resultRank[i] = r / m;
                // 对与任意一个节点，找一个和其相邻的节点集合
                for (int i = 0; i < m; i++) {
                    int count = 0;// 统计和节点i相连的节点个数
                    for (int j = 0; j < m; j++) {
                        if (numb[i][j] != 0) {
                            count++;
                        }
                    }
                    if (count > 0) {
                        for (int j = 0; j < m; j++) {
                            if (numb[i][j] != 0) {double value=(1 - r)*nowRank[i]/ count;
                                resultRank[j] +=value;
                            }
                        }
                    } else {
                        for(int j=0;j<m;j++){
                            resultRank[j]+=(1-r)*nowRank[i]/m;
                        }
                    }
                    //nowRank=resultRank;-----fuck you
                    for(int j=0;j<m;j++){
                        nowRank[j]=resultRank[j];
                    }
                    System.out.println("遍历完一个节点------------------------------------------------");
                    //-------
                }
                for(int i=0;i<m;i++){
                    System.out.print(";  节点"+i+" 概率:"+resultRank[i]);
                }
                System.out.println("
-------------------------------------");
            }

        }
    }
}

 参考：http://blog.jobbole.com/71431/

实际上，google发明Map-Reduce最初就是为了分布式计算大规模网页的pagerank，Map-Reduce的pagerank有很多实现方式，我这里计算一种简单的。

考虑转移矩阵是一个很多的稀疏矩阵，我们可以用稀疏矩阵的形式表示，我们把web图中的每一个网页及其链出的网页作为一行，这样第四节中的web图结构用如下方式表示：

1 2 3 4

1 A    B    C    D 2 B    A    D 3 C    C 4 D    B    C

A有三条出链，分布指向A、B、C，实际上，我们爬取的网页结构数据就是这样的。

1、Map阶段

Map操作的每一行，对所有出链发射当前网页概率值的1/k，k是当前网页的出链数，比如对第一行输出<B，1/3*1/4>,<C，1/3*1/4>,<D，1/3*1/4>;

2、Reduce阶段

Reduce操作收集网页id相同的值，累加并按权重计算，pj=a*(p1+p2+…Pm)+(1-a)*1/n，其中m是指向网页j的网页j数，n所有网页数。

思路就是这么简单，但是实践的时候，怎样在Map阶段知道当前行网页的概率值，需要一个单独的文件专门保存上一轮的概率分布值，先进行一次排序，让出链行与概率值按网页id出现在同一Mapper里面，整个流程如下：